Задача 2.36.
Техническое устройство выходит из строя, образуя простейший поток отказов с плотностью l. В произвольный момент времени исправной работы устройства инженер засекает время (пускает таймер). Найти закон распределения времени Т, которое придется ждать, его математическое ожидание mt и среднее квадратическое отклонение st.
Решение.
Напоминание. Простейший (стационарный пуассоновский) поток является потоком Пальма, –– поток событий, у которого промежутки между соседними событиями представляют собой независимые случайные величины.
Плотность распределения времени ожидания будет такая же, как плотность распределения промежутка между отказами:
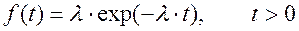 ,
,
что объясняется тем, что «будущее» в простейшем потоке никак не зависит от «прошлого», в частности от того, сколько времени тому назад произошел предыдущий отказ.
Для показательного закона имеем:
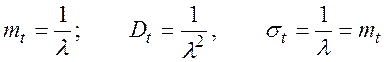
Дата добавления: 2015-05-26; просмотров: 553;
