Задача 2.40.
Рассматривается предельный стационарный режим работы n-канальной системы массового обслуживания с отказами. Плотность потока заявок l, плотность «потока обслуживания» (потока освобождения одного занятого канала) равна m.
Требуется найти следующие характеристики СМО:
среднее число k занятых каналов;
вероятность Pзан того, что произвольно взятый канал будет занят;
среднее время 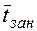 занятости одного (произвольно выбранного) канала;
занятости одного (произвольно выбранного) канала;
среднее время 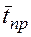 простоя канала.
простоя канала.
Решение.
1) Для любой СМО, в которой каждая заявка может обслуживаться только одним каналом, среднее число заявок l0 , обслуживаемых в единицу времени, определяется как произведение среднего числа 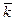 занятых каналов на плотность потока обслуживаний:
занятых каналов на плотность потока обслуживаний:
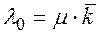
Вероятность обслуживания произвольно выбранной заявки равна отношению плотности потока обслуживаемых заявок к плотности потока поступающих заявок:
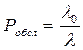 , откуда
, откуда 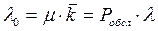 , следовательно
, следовательно 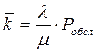 ,
,
или 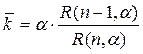 , где
, где 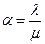 ,
, 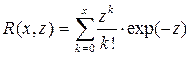
Выражение для среднего числа занятых каналов можно получить и из формулы:
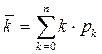 , где рк определяется по формуле:
, где рк определяется по формуле:
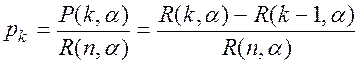 , k=0, 1, …, n
, k=0, 1, …, n
2) Обозначим вероятность того, что произвольно взятый канал занят обслуживанием какой-то заявки, через Рзан. Очевидно, что эта вероятность одинакова для всех каналов, тогда:
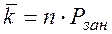 ,
,
откуда:
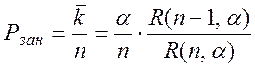
3) Среднее время занятости одного канала 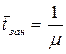 , т.е. равно среднему времени обслуживания заявки.
, т.е. равно среднему времени обслуживания заявки.
4) Среднее время простоя канала 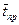 определяется из условия:
определяется из условия:
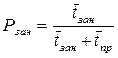 , (вероятность того, что все каналы заняты),
, (вероятность того, что все каналы заняты),
откуда
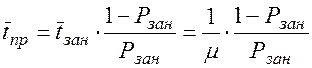 .
.
Дата добавления: 2015-05-26; просмотров: 1190;
