Методы оценки надежности нерезервированных невосстанавливаемых систем.

5.1. Сложные технические системы и определение их надежности.

Обычные методы количественной оценки критериев надежности сложных систем базируются на том, что отказы системы образуют простейший поток событий.

Все системы условно можно разделить на два класса:

системы без избыточности,

системы с избыточностью.

Под системами без избыточности будем понимать такие системы, у которых выход из строя любого элемента приводит к выходу из строя всей системы. Системы с избыточностью способны продолжать свое функционирование в случае выхода из строя некоторых ее элементов.

Системы без избыточности, отказ которых не всегда происходит одновременно с отказами отдельных элементов, называются последовательными системами с накоплением нарушений или просто системами с накоплением нарушений.

Таким образом, системы, не имеющие избыточности, (последовательные системы) можно в свою очередь разбить на два класса:

последовательные системы без накопления нарушений (системы, у которых появление нарушений в работе элементов связано с одновременным отказом системы);

последовательные системы с накоплением нарушений, когда нарушение в смысле постепенного ухода параметров элементов по тем или иным причинам понимается как постепенный отказ.

Далее рассматриваются системы без избыточности и без накопления нарушений.

Система без избыточности с точки зрения надежности рассматривается как совокупность последовательно соединенных элементов. Это означает, что выход из стоя любого элемента выводит из строя всю систему. При таком подходе в ряде случаев для реальных систем значения критериев надежности получаются заниженными, т.к. в большинстве сложных технических систем отказ многих элементов не приводит к одновременному отказу всей системы.

Вполне естественно предположить, что функциональное усложнение системы может привести как к повышению, так и к снижению надежности. Чем больше число элементов в системе, тем, в общем случае, ниже ее надежность при прочих равных условиях.

Все это обуславливает необходимость разработки таких методов оценки надежности, которые отражали бы структурные (функциональные) особенности системы.

Важнейшее значение при оценке надежности играет понятие состояния системы.

Под состоянием системы в момент времени t понимается множество количественных значений параметров элементов системы, которые в этот момент полностью определяют ее функциональные возможности.

Под функцией качества чаще всего понимают или совокупность параметров выходного сигнала системы, или совокупность параметров, характеризующих свойство продукта, производимого данной (технической) системой.

Надежностью системы будем называть вероятность того, что в течение времени T ³ t система выполнит любое из требований, для которых она создана.

При таком определении надежность представляет собой некую усредненную интегральную характеристику и можно представить две системы надежные на рассматриваемом интервале времени (согласно определению), но неравнонадежные в сравнении.

Решая задачу по определению надежности, во многих случаях можно рассматривать только изменения состояния системы в результате внезапных отказов ее элементов, полагая, что постепенные отказы отсутствуют. Такой подход справедлив для интервалов времени, не включающих границы ресурсов элементов по долговечности. Естественно, можно решать и задачу определения надежности технической системы с учетом как внезапных отказов, так и отказов элементов по причине старения.

При таких предположениях, если система состоит из n элементов (каждый из которых может находиться лишь в одном из двух состояний: исправен или неисправен), система может иметь 2ⁿ состояния

Напомним, что интенсивностью отказов называется отношение числа отказавших образцов аппаратуры (устройств, элементов, систем) в единицу времени к среднему числу образцов, исправно работающих в данный отрезок времени при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

Напомним так же, что интенсивность внезапных отказов элементов в процессе эксплуатации, (когда фазой приработки и фазой старения можно пренебречь) сохраняет постоянное во времени значение.

Предполагается, что вероятность самостоятельного перехода любого элемента системы из неисправного состояния в исправное равна нулю, т.е. неисправное состояние является поглощающим (рассматриваются невосстанавливаемые системы).

Для последовательных систем без накопления нарушений, принимая, что времена отказов элементов являются независимыми случайными величинами, в силу условий отсутствия последействия и ординарности потока отказов надежность системы можно выразить через надежность каждого элемента:

(5.1)
где P(t) –– надежность системы на момент t; p_j(t) ––надежность j-го элемента системы.

Откуда следует, что надежность технической системы без избыточности зависит от надежности всех элементов и становится равной нулю в случае равенства нулю надежности хотя бы одного из p_j(t).

По определению плотность распределения отказов системы равна отношению:

, тогда, с учетом (5.1), имеем: (5.2)

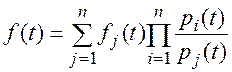(5.3)
где –– плотность распределения отказов j–го элемента системы.

Вспомним, что производная произведения имеет вид: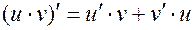

Докажем справедливость (5.3). Пусть n=3, тогда:

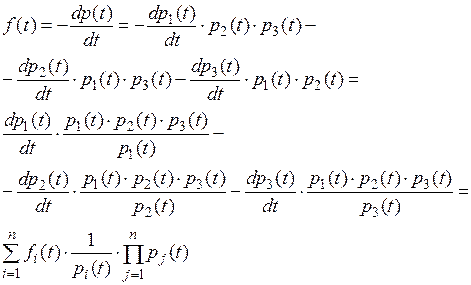(5.4)
Поскольку интенсивность отказов системы , с учетом (5.1) и (5.4) получим:

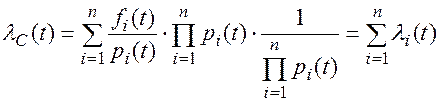(5.5)
т.е. интенсивность отказов l_С(t) последовательной системы без избыточности равна сумме интенсивностей отказов, входящих в эту систему элементов.

Еще раз напомним, что полученные зависимости справедливы в пределах принятых ранее допущений:

выход из строя элемента приводит к выходу из строя всей системы;

моменты выхода элементов из строя представляют собой независимые случайные величины.

Таким образом, приведенные расчетные соотношения справедливы для сложных технических систем (для оценки времени их безотказной работы) одноразового действия.

5.2. Оценка надежности последовательных систем без накопления нарушений при наличии только внезапных отказов элементов.

Полученная в предыдущем параграфе формула для оценки надежности системы, опирается на надежность ее элементов:

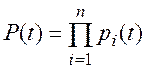(5.6)
В общем виде надежность одного элемента определяется соотношением:

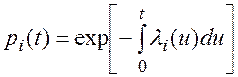(5.7)
После подстановки (5.7) в (5.6), получим:

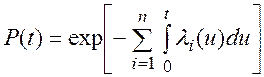(5.8)
В случае, когда поток отказов элементов является простейшим, т.е. ординарным, стационарным (l_i не зависит от времени t) и не обладает последействием, что характерно для потоков внезапных отказов элементов, надежность (вероятность безотказной работы) i-го элемента определяется по формуле:

(5.9)
Надежность системы в этом случае определится соотношением:

(5.10)
используя обозначение 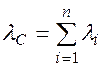, можно записать:

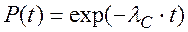(5.11)
В предположении о стационарности потока отказов, l_i=const, (интенсивности отказов элементов не зависят от времени) среднее время Т_С безотказной работы системы и функция частоты отказов a_С(t) могут быть вычислены по формулам:

(5.12)

,

или ,

или ,

,

тогда:

(5.13)
Оценим границы изменения надежности системы при учете только внезапных отказов ее элементов.

Верхнюю границу значений надежности определим в предположении о том, что система состоит всего из двух условных элементов: один условный элемент представляет собой объединение n-1 элемента, интенсивности отказов которых принимаем равными нулю, т.е. первый условный элемент абсолютно надежен, а второй условный элемент системы представляет собой реальный элемент с максимальным значением интенсивности отказов l_max среди всех n элементов системы.

Тогда верхнее значение надежности системы будет равно:

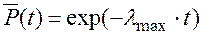(5.14)
Нижнюю границу значений надежности технической системы , определим в предположении о том, что все n элементов системы имеют одинаковые интенсивности отказов, равные интенсивности отказов самого ненадежного элемента, т.е. максимальную интенсивность отказов среди всех n элементов:

(5.15)
Тогда интервал возможных значений технической системы по внезапным отказам определится соотношением:

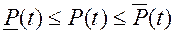(5.16)

5.3. Оценка надежности последовательных сложных систем без накопления нарушений с учетом старения (износа) элементов.

В реальных условиях на работу технической системы будут оказывать влияние не только аварийные отказы элементов, но и отказы по причине старения.

Будем полагать, что аварийные отказы и отказы по причине износа независимы и введем обозначения:

Q₁(t), Q₂(t), …, Q_n(t) –– вероятности выхода из строя элементов в результате внезапных отказов,

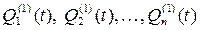–– вероятности выхода элементов из строя в результате старения,

p₁(t), p₂(t),…,p_n(t) –– вероятности безотказной работы элемента по аварийности,

–– вероятности безотказной работы элементов по износу.

Тогда вероятность безотказной работы i-го элемента определится соотношением:

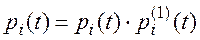(5.17)
С учетом принятых ранее допущений для системы в целом имеем:

(5.18)
Поскольку было принято, что надежность i-го элемента по внезапным отказам , уравнение для оценки надежности системы с учетом внезапных отказов и отказов вследствие старения элементов принимает вид:

(5.19)
Пусть надежность i-го элемента по старению определяется вместо нормального закона распределения, выражением:

(5.20)
Тогда формула для оценки надежности системы с учетом внезапных отказов элементов и отказов по причине их старения принимает вид:

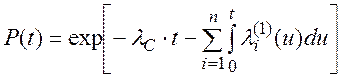(5.21)
Откуда следует, что функция интенсивности отказов системы l_С(t) при наличии аварийных отказов и отказов по старению, в предположении, что эти отказы, а так же и отказы элементов, являются независимыми событиями, определяется уравнением:

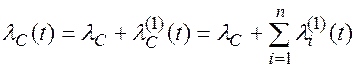(5.22)
где 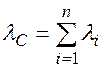–– интенсивность отказов системы только по причине внезапных отказов элементов.

Суммарная интенсивность аварийных отказов и отказов по старению для одного i-го элемента определяется уравнением:

(5.23)
Надежность одного элемента с учетом аварийных отказов и отказов по старению можно вычислить по формуле:

(5.24)
Найдем верхнюю 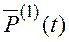и нижнюю границы надежности с учетом эффекта старения элементов.

Максимальная величина надежности (вероятности безотказной работы системы в течение времени t с момента ее включения) будет определяться надежностью системы, рассчитанной в предположении о наличии только внезапных отказов и надежностью самого ненадежного элемента по старению , т.е.

(5.25)
Нижняя граница надежности системы определяется в предположении, что все n элементов по старению имеют надежность, равную надежности наименее надежного элемента, а по внезапным отказам надежность определяется по прежним методикам:

(5.26)
следовательно,

(5.27)
или

(5.28)
Абсолютный интервал возможных значений надежности технической системы, рассчитанный с учетом внезапных отказов элементов и их отказов по старению определяется на основании объединения (5.16) и (5.27):

(5.29)