Надежность элементов технических систем.

4.1. Основные виды отказов элементов технических систем.

Все отказы элементов (устройств) технических систем можно подразделить на три группы:

отказы по вине дефектов производства;

аварии и поломки (внезапные отказы);

аварии по причине старения (постепенные отказы).

Кроме того, отказы бывают независимыми, т.е. не являющимися следствием ранее появившихся отказов, зависимыми, т.е. появившимися в результате ранее появившихся отказов. На практике так же имеют место отказы самопроизвольно возникающие и самопроизвольно исчезающие (мерцающие отказы).

4.2. Кривая распределения отказов элементов.

Наличие трех независимых групп отказов, каждая из которых имеет свои особенности, определяет вид характерной кривой изменения интенсивности отказов (рис.4.1) и кривой изменения надежности (рис. 4.2).

Рис. 4.1. Типичная кривая изменения интенсивности отказов.

Рис. 4.2. Вероятность безотказной работы (надежность элемента).

Отказы по вине производства проявляются, как правило, на начальном этапе эксплуатации, их интенсивность убывает со временем.

Интенсивность внезапных отказов элементов почти не зависит от времени, т.е. является величиной постоянной.

Отказы по причине старения начинают влиять на надежность элементов технических систем с определенного момента времени.

Иногда с экономической точки зрения целесообразнее допустить некоторую возможность отказов по вине производственных дефектов, чем создавать новую, сложную и дорогую контрольную аппаратуру. В таком случае необходимо искать оптимальное решение.

Аналогичное противоречие имеет место при попытке сокращения внезапных отказов, поскольку это будет связано с разработкой элементов, способных работать в жестких условиях, что, естественно, связано с дополнительными трудностями и затратами.

В конечном счете задача определения необходимого уровня надежности должна быть решена как задача поиска оптимального решения в координатах «эффективность –– стоимость».

В дальнейшем общий поток отказов рассматривается как суперпозиция трех видов отказов без их взаимного влияния.

4.3. Особенности распределения отказов элементов по вине производства.

Отличительной особенностью распределения отказов по технологическим причинам производства элементов технических систем является их убывание по мере увеличения срока эксплуатации системы.

Такому условию в большей степени удовлетворяет распределение Вейбулла, для которого:

плотность распределения

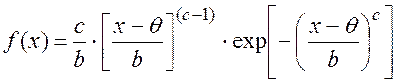(4.1)
где ,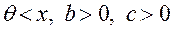

функция распределения (функция отказов или ненадежности)

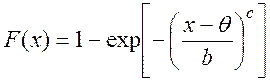(4.2)
функция надежности

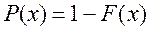
интенсивность отказов:

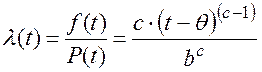(4.3)

4.4. Законы распределения внезапных отказов элементов.

Ранее (3.19) было определено, что вероятность исправной работы элемента технической системы в интервале времени (0, t) определяется соотношением:

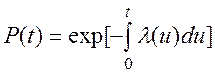(4.4)
Рассмотрим подробнее характеристику l(t). Согласно (3.15):

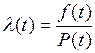, (4.5)

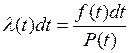(4.6)
где f(t) –– плотность распределения времени исправной работы.

Определим:

событие А, состоящее в том, что время T исправной работы (случайная величина) будет не меньше конкретного значения t,

событие В, заключающееся в том, что выход из строя элемента произойдет в момент t £ T < t+dt

Согласно теореме умножения вероятностей:

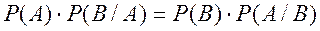(4.7)
откуда

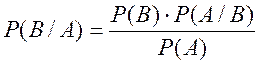(4.8)

где Р(B/A) –– условная вероятность отказа в интервале (t, t + dt) при условии, что к моменту t устройство было исправно;

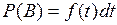(4.9)
представляет собой безусловную вероятность отказа на интервале времени (t, t+dt),

Р(A/B)=1 –– вероятность исправной работы элемента в интервале (0, t), при условии, что он вышел из строя в интервале (t, t + dt);

Р(A)=Р(T ³ t)=P(t) –– безусловная вероятность исправной работы в течение времени (0, t).

Тогда

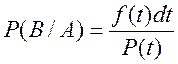(4.10)
Сравнивая (4.3) и (4.7), имеем:

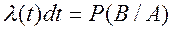(4.11)
т.е. l(t)dt есть вероятность выхода элемента из строя в интервале времени (t, t+dt) при условии, что к моменту t он был исправен. Следовательно, по аналогии с (4.5) функцию l(t) можно определить как условную плотность распределения времени отказов элемента.

Опыт эксплуатации и испытаний на надежность технических систем показывает, что внезапные отказы обладают замечательным свойством: интенсивность внезапных отказов элементов практически постоянна на всем этапе их эксплуатации.

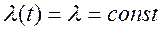(4.12)
тогда из (4.4) следует, что при внезапных отказах вероятность исправной работы элемента технической системы будет равна:

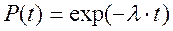(4.13)
Соответственно, вероятность выхода из строя элемента и плотность распределения времени исправной работы определяются формулами:

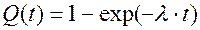(4.14)

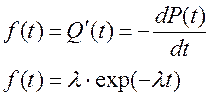(4.15)
Интенсивность отказов имеет размерность, обратную размерности случайной величины, т.е. 1/ время.

В теории надежности часто вместо l используют величину Т_с, представляющую собой ожидаемый интервал времени до первого отказа или среднее время между отказами однотипных элементов (наработка элемента на отказ).

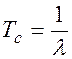(4.16)
Из общей теории вероятностей известно, что математическое ожидание случайной величины (времени непрерывной работы элемента) Т_с и его дисперсия D определяются с учетом того, что случайное время выхода элемента из строя в данном случае изменяется в пределах от 0 до t.

Расстояние Т между двумя соседними событиями в простейшем потоке есть непрерывная случайная величина, распределенная по показательному закону с плотностью:

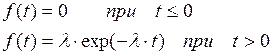(4.17)
При этом:

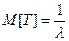(4.18)

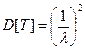(4.19)

Экспоненциальное распределение обладает еще одним свойством: вероятность исправной работы в интервале времени от t до t+t, которому предшествует исправная работа в интервале времени (0, t), не зависит от момента t, а зависит только от длины самого интервала (t+t)-t=t.

Условная вероятность 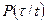того, что элемент сохраняет свою работоспособность в течение интервала времени (t, t+t) при условии, что к моменту t он был работоспособен, определяется по формуле полной вероятности:

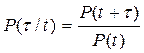, (4.20)

где P(t+t) –– вероятность безотказной работы элемента на всем эксплуатационном интервале (0, t+t);

P(t) –– вероятность безотказной работы элемента на интервале (0, t).

Тогда:

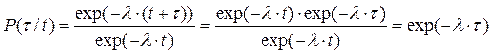(4.21)

4.5. Законы распределения постепенных отказов (отказов по старению).

Постепенные отказы могут иметь различные законы распределения. Причиной постепенных отказов являются необратимые физико-химические процессы, протекающие в структуре элементов технически систем и приводящие к изменению их входных параметров или характеристик.

Поскольку изменение параметра во времени может носить случайный характер, то кривую изменения конкретного параметра данного элемента следует считать реализацией случайной функции X(t).

Случайной функцией X(t) называется функция, значение которой при каждом данном значении аргумента t является случайной величиной.

Характер распределения времени исправной работы элемента по старению (износу) зависит от начального распределения свойств элемента по параметру X в точке t=0 и вида случайного процесса изменения данного свойства.

Таким образом, в простейшей постановке задача определения закона распределения времени исправной работы элемента технической системы по старению сводится к задаче нахождения искомого закона по известным законам распределения параметра в одном или нескольких сечениях t_j случайной функции X(t).

4.6. Дифференциальный закон распределения времени исправной работы элемента с учетом отказов по вине производства, внезапных отказов и отказов по причине старения.

Сделаем следующие допущения.

Распределение времени отказов по вине производства распределено по закону Вейбулла с параметрами:

q = 0, b ³ 1, c @ 0.5, tÎ[0, t₁].

где t₁ –– окончание этапа приработки технической системы.

Распределение времени возникновения неисправностей в результате аварий и поломок (внезапные отказы) подчинено экспоненциальному закону с параметром l для tÎ[t₁, t₂],

где t₂ –– начало этапа старения элементов системы.

Распределение времени отказов при учете только аварий по причине старения (износа) подчинено нормальному закону с параметрами T₀ и s_0.

События, заключающиеся в выходе из стоя элементов по причине производства, внезапных отказов и по причине старения, совместны и независимы.

Принятые допущения не вносят существенных ошибок в определение показателей надежности технических систем по следующим причинам:

внезапные отказы редки, а их интенсивность во времени постоянна;

число факторов, влияющих на выход элементов из строя по причине старения велико и все причины практически равнозначны, что позволяет сделать вывод о том, что плотность распределения времени исправной работы элемента по старению подчинена закону, близкому к нормальному;

совместность выхода из строя элементов по производственным дефектам, старению и по причине внезапной аварии не вызывает сомнений, но случаи выхода элементов из строя по трем причинам чрезвычайно редки, поэтому условием совместности иногда допустимо пренебречь.

Таким образом, любой элемент можно представить в виде системы, состоящей из трех условных элементов, соединенных в смысле надежности последовательно.

Будем полагать, что отказы одного условного элемента происходят только в результате производственных недоработок, второго –– по причине аварий или поломок, а третьего–– только в результате износа или старения.

Плотность распределения времени исправной работы первого элемента:

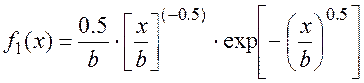(4.22)
для второго элемента:

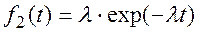(4.23)
для третьего элемента:

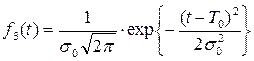(4.24)
Надежность этих условных элементов определяется соответственно:

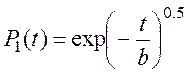(4.25)

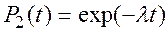(4.26)

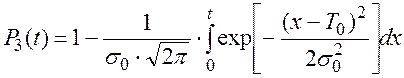(4.27)

Система, состоящая из трех последовательно соединенных условных элементов, будет исправной только тогда, когда все три элемента будут исправны.

В этом случае формула для определения вероятности исправной работы элемента (состоящего из трех условных элементов) будет иметь вид:

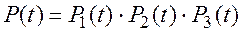(4.28)
Плотность распределения времени исправной работы определится через вероятность соотношением:

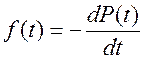(4.29)
тогда, учитывая:

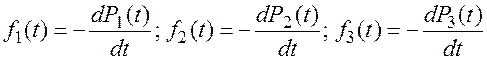(4.30)
получим:

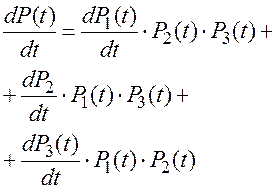(4.31)

4.7. Расчетно-графическая работа № 1.

Определение показателей надежности элементов по опытным данным.

Дано:

N₀ –– число элементов, участвующих в испытании;

t_i –– время исправной работы i-го элемента, i=1,2,3,…,N₀.

Требуется определить.

l(t) –– интенсивность отказов как функцию времени;

f(t) –– плотность распределения времени исправной работы элемента;

P(t) –– вероятность безотказной работы элемента в течение времени t;

T_с –– среднее время безотказной работы (наработка на отказ);

f(t) –– плотность распределения времени до отказа;

l(t) –– интенсивность отказов на момент t.

Основные зависимости.

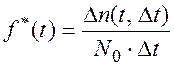
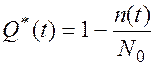
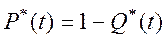
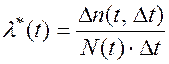
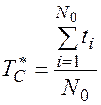
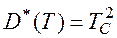
В каждом варианте расчетной работы набор чисел, соответствующий времени выхода из строя элементов выбирается с помощью датчика случайных чисел компьютера.

Вопросы для самоконтроля.

Назовите три характерные группы отказов элементов технических систем.

Дайте определение частоты и интенсивности отказов элементов.

Объясните поведение функций изменения частоты и интенсивности отказов элементов во времени.

В чем состоят особенности распределения отказов элементов технических систем по вине производства.

Назовите характерные особенности распределения отказов элементов по старению.

Объясните допущения, принимаемые при определении дифференциального закона распределения элементов с учетом внезапных отказов и отказов по старению.

В чем состоит существо методики определения количественных характеристик надежности элементов технических систем с учетом старения.

Приведите примеры экспериментального определения параметров закона распределения времени исправной работы элементов технических систем.