Задача 2.41.

Рассматривается работа автозаправочной станции (АЗС), на которой имеется 4 раздаточные колонки (n=4). Заправка одной автомашины длится в среднем 3 минуты. В среднем на АЗС каждую минуту прибывает автомашина для заправки. Число мест в очереди практически не ограничено. Все машины, вставшие в очередь «терпеливо» дожидаются заправки.

Требуется определить:

среднее время, проходящее с момента прибытия машины на АЗС до ее заправки;

среднее число занятых мест ;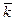

среднее число автомашин в очереди ;

среднее время простоя колонки между заправками.

Решение.

Работа АЗС может рассматриваться как функционирование чистой СМО с ожиданием при числе каналов n=4, и параметре потока заявок l=1(1/мин). Параметр потока обслуживаний m=1/3 (1/мин). В этом случае:

.

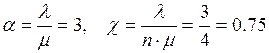Поскольку c < 1, то при t®¥ существует предельный режим.

В рассматриваемой постановке вероятность обслуживания любой заявки будет равна единице (Р_обс=1), так как рано или поздно машина, стоящая в очереди, будет заправлена. Среднее число занятых каналов равно (см. предыдущую задачу):

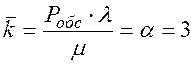
Среднее число машин , ожидающих в очереди, равно (2.107):

Воспользуемся свойством бесконечной геометрической прогрессии для х<1, что согласуется с тем, что c<1:

и найдем сумму вида:

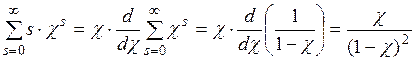
Тогда:

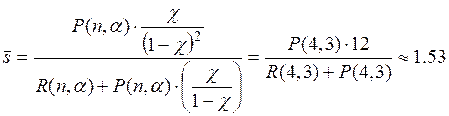
Среднее время пребывания машины у АЗС будет равно: 3+1.53=4.53 мин.

Среднее число машин, ожидающих заправки или заправляющихся (находящихся на территории АЗС) равно:

Среднее время простоя заправочной колонки:

, поскольку

Замечание.

Выражение для функции R(x, z) дано в задаче 2.40.

Основные понятия и количественные характеристики надежности технических систем

3.1. Предмет надежности.

Теория надежности представляет собой науку, изучающую закономерности нарушения условий функционирования систем (устройств, элементов) в течение их жизненного цикла.

Техническая система –– совокупность взаимосвязанных элементов (объектов, устройств), обеспечивающих выполнение конкретных практических задач.

Устройством называется законченная конструкция, которая, являясь частью системы, имеет самостоятельное целевое назначение.

Элементы –– это части системы или устройства, которые выполняют в нем определенные функции и не могут иметь самостоятельного (вне связи с другими элементами или устройствами) применение.

Надежность –– свойство системы (устройства, элемента), обусловленное, главным образом, ее безотказностью и ремонтопригодностью, обеспечивающих требуемую эффективность функционирования системы в течение заданного интервала времени.

3.2. Причины недостаточной надежности технических систем.

Основными причинами отказов технических систем являются внезапные (случайные) отказы, отказы вследствие ухудшения характеристик элементов (старение, износ), а также по вине скрытых производственных дефектов, характерных для начального периода эксплуатации, или нарушения условий эксплуатации.

Возрастание интенсивности отказов технических систем связано, как правило, с ужесточением условий их функционирования (эксплуатации) и с недостаточной квалификацией обслуживающего персонала.

В целом, все причины, приводящие к снижению надежности технических систем, можно разделить на следующие: конструктивные, производственные, эксплуатационные, организационные.

Конструктивные причины: низкая надежность элементной базы, неправильный выбор элементов, неудачное схемно-компоновочное решение, недостаточная унификация элементов, недостаточная отработка технологий на этапах испытаний.

Производственные причины: нарушение качества материалов, недостаточный контроль входных параметров, недостаточная отработка технологии производства и сборки устройств, общая низкая культура производства.

Эксплуатационные причины: низкая квалификация технического персонала, низкая эффективность контрольно––проверочной аппаратуры, нарушение условий эксплуатации.

Организационные причины: отсутствие требований по поддержанию заданных показателей надежности, несоответствие заводских испытаний реальным условиям эксплуатации, неритмичность эксплуатации.

3.3. Цена надежности.

Стоимость технической системы, как правило, определяется стоимостью ее создания (строительства) и стоимостью эксплуатации системы и зависит от надежности системы.

C_å (Р)= C₀ (Р) + C_э (Р) (3.1)

где C_å (Р) –– общая стоимость технической системы;

C₀(Р) –– стоимость создания технической системы;

C_э(Р) –– стоимость эксплуатации технической системы,

Р –– надежность системы.

Расходы, связанные с созданием технической системы, являются функцией требований по ее надежности. Чем выше требования по надежности системы, тем выше ее стоимость, т.е. функция C₀ (P) –– неубывающая функция надежности системы (рис. 3.1).

Рис. 3.1. Изменение суммарной стоимости С_S системы в зависимости от ее надежности Р, затрат на эксплуатацию С_Э и создание системы С₀.

Рациональное распределение средств на повышение надежности технических систем на этапе проектирования, изготовления, испытания и эксплуатации может привести к существенной экономии суммарных расходов обеспечения функционирования системы.

Особенно следует отметить расходы на ликвидацию последствий возможных аварий с техническими системами. Математическое ожидание этих расходов M зависит от вероятности W аварии (которая в свою очередь зависит от надежности, поскольку отказ некоторых элементов или узлов способен не просто остановить систему, но и вызвать аварийную ситуацию с последствиями негативного воздействия на среду и население) и от стоимости C_a ликвидации последствий аварии.

(3.2)

3.4. Основные понятия теории надежности.

Теория надежности в большинстве случаев оперирует случайными величинами, поэтому большая часть понятий и определений связана с понятийным аппаратом теории вероятностей.

Отказ –– полная или частичная утрата работоспособности элементом, устройством или рассматриваемой технической системой.

Исправность –– состояние системы, при котором она в данный момент времени соответствует всем требованиям, установленным в отношении как основных параметров, так и «второстепенных».

Работоспособность –– состояние системы, при котором она в данный момент времени соответствует всем требованиям, установленным в отношении ее основных параметров.

Безотказность –– свойство системы сохранять работоспособность в течение заданного интервала времени в определенных условиях эксплуатации.

Неисправность –– состояние системы, при котором она в данный момент времени не соответствует хотя бы одному из требований, установленных в отношении как основных параметров, так и «второстепенных».

3.5. Основные количественные характеристики надежности и связь между ними.

Основной количественной характеристикой надежности является вероятность безотказной работы, определяемая как вероятность P(t) нахождения системы в исправном состоянии в течение времени T ³ t, где Т –– случайная величина продолжительности работы системы до отказа, t –– детерминированная величина текущего времени или его конкретное значение:

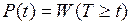(3.3)
где W(T) –– вероятность реализации события, заключающегося в том, что отказ системы не произойдет ранее t.

Функция P(t) обладает следующими свойствами:

P(0) = 1, P(¥) = 0, P(t₂) £ P(t₁) при t₂ > t₁,

т.е. функция P(t) –– невозрастающая функция времени.

Эту функцию часто называют функцией надежности или просто надежностью технической системы.

Характеристикой, противоположной надежности, является вероятность отказа Q(t), как вероятность того, что устройство или техническая система откажет в течение времени T < t :

(3.4)
Свойства функции Q(t) : Q(0) = 0, Q(¥) = 1, Q(t₂) ³ Q(t₁) при t₂ > t₁ .

Таким образом, функция Q(t) представляет собой функцию распределения времени исправной работы системы F(t) (см. выражение (2.20) .

Очевидно: Q(t) + P(t) = 1; Q(t)=1-P(t)

(3.5)
т.е. система может находиться либо в исправном, либо в неисправном состоянии.

Рис. 3.2. Характер изменения функций надежности и отказов во времени.

Плотность f(t) распределения времени работы системы до отказа согласно определению плотности из классической теории вероятностей имеет вид (2.21):

(3.6)
Наряду с аналитическими методами определения различных параметров надежности широко используются статистические методы, с помощью которых определяются так называемые статистические характеристики надежности систем. Эти характеристики представляют собой результаты обработки экспериментальных данных или данных прямых наблюдений.

Поскольку в эксперименте невозможно произвести наблюдения при t®¥ или на бесконечно малом временном интервале Dt®0, а также при бесконечно большом числе испытываемых систем, то статистические характеристики следует рассматривать как оценочные или приближенные к теоретическим.

Статистическая плотность отказов 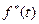в теории надежности определяют в виде отношения:

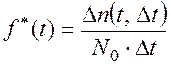(3.7)
где Dn(t, Dt) –– число отказавших элементов на интервале Dt (от момента времени t до момента t+Dt); N₀ –– общее число элементов, выставленных на испытания; Dt ––интервал времени проведения испытаний или наблюдений.

Рис. 3.3. Порядок вычисления количества отказавших элементов Dn.

Статистически функция распределения времени исправной работы Q*(t) системы оценивается как отношение числа устройств n(t), вышедших из строя за время от начала испытаний до некоторого момента t, к общему числу элементов или устройств N₀, поставленных на испытание:

(3.8)
Величину Q*(t) называют частостью отказов, которая является оценкой функции распределения отказов или вероятности отказа.

Очевидно, что чем больше проведено число независимых испытаний, тем ближе величина частости к соответствующему значению вероятности. В теории вероятностей такой характер приближения одних величин к другим чрезвычайно употребителен и для его описания введен специальный термин –– сходимость по вероятности.

Согласно первой предельной теореме (закон больших чисел), последовательность случайных величин x_n сходится по вероятности к величине J, если при сколь угодно малом e>0 вероятность неравенства ½x_n - J½< e с увеличением n неограниченно приближается к единице.

Таким образом, можно утверждать, что с увеличением числа опытов частость события сходится к его вероятности по вероятности.

Одной из характеристик надежности технических систем является частота отказов, в дальнейшем обозначаемая a(t).

Частотой отказов а^*(t) называется отношение числа отказавших образцов в единицу времени к числу образцов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

(3.9)
Выражение (3.9) является статистическим определением частоты отказов. Вместе с тем этой характеристике можно придать вероятностное определение.

Число отказавших образцов на интервале Dt может быть определено по формуле:

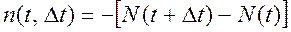(3.10)
где N(t) –– число образцов, исправно работающих к моменту t; N(t+Dt) –– число образцов, исправно работающих к моменту t+Dt.

При достаточно большом числе образцов N₀ справедливы следующие соотношения:

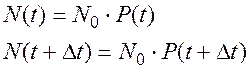(3.11)
Подставляя (3.10) в (3.9) и учитывая (3.11), получим:

(3.12)
Устремляя к нулевому пределу интервал Dt, получим с учетом определения Dn(t, Dt), принятого в (3.7):

(3.13)
или

(3.14)
Последнее равенство подтверждает идентичность (3.7), (3.9).

Из выражения (3.14) следует утверждение, что частота отказов представляет собой плотность (3.6) распределения времени работы системы до ее отказа.

Наиболее употребительной в теории надежности является такая характеристика, как интенсивность отказов:

(3.15)
т.е. l(t) является условной плотностью распределения вероятности исправной работы системы, вычисленной при условии, что к моменту t система была исправна.

Статистической интерпретацией интенсивности отказов l(t)* является отношение числа однотипных устройств Dn(Dt) , вышедших из строя в интервале времени Dt , к числу устройств S(t) из общего числа N , поставленных на испытания, продолжающих к моменту времени t оставаться исправными, умноженному на длину интервала Dt, при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

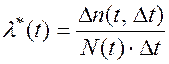(3.16)
Разделив числитель и знаменатель (3.16) на N₀, получим:

,

или

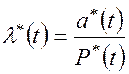(3.17)
Таким образом, интенсивность отказов определяется как отношение частоты отказов (3.9) к статистической оценке вероятности исправной работы рассматриваемого элемента или устройства 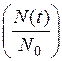. Типичная кривая изменения интенсивности отказов технических систем представлена на рисунке 3.4.

Рис. 3.4. Типовая зависимость интенсивности отказов технических систем от времени.

Как видно из рис. 3.4 кривая l(t) имеет три характерных участка. Первый участок (от 0 до t₁) –– участок приработки, второй участок (от t₁ до t₂) –– участок нормальной эксплуатации системы, третий временной интервал (от t₂ и далее) –– участок старения системы. Здесь уместно отметить, что в период нормальной работы системы (от t₁ до t₂) как правило интенсивность отказов не зависит от времени, l=const.

Выражение (3.15) с учетом (3.6) приобретает вид:

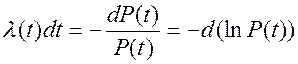(3.18)
Интегрируя (3.18) при начальном условии P(0) = 1, получим:

или

Поскольку т.е. С=1.

Нижний предел интегрирования равен 0, т.к. отсчет времени производится от момента включения системы в работу.

Верхний предел определяется аргументом функции P(t) т.е. значением аргумента t.

Окончательно получаем:

(3.19)
Выражение (3.19) определяет вероятность безотказной работы технических систем и является одним из основных в теории надежности.

Среднее время до отказа технической системы Т_С определяется как его математическое ожидание (2.26) с нижним пределом интегрирования, равным нулю:

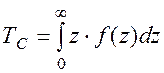(3.20)
Статистической интерпретацией среднего времени до первого отказа является среднее арифметическое значение времени работы устройства до ее первого отказа:

(3.21)
где R_i –– называют частостью времени отказов t_i; t_i –– время работы i-го элемента до первого отказа; N₀ –– число элементов, поставленных на испытание.

Выражение (3.20) можно представить в ином виде, подставив выражение плотности f(t) согласно (3.6):

(3.22)
Произведем интегрирование по частям:

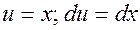
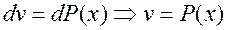
(3.23)
Дисперсия D[T] случайного времени Т безотказной работы системы:

(3.24)
где Т –– случайное время безотказной работы системы; Т_с –– математическое ожидание времени работы системы до отказа; f(x) –– дифференциальный закон распределения случайного времени безотказной работы системы.

Для случая распределения случайной величины по закону Пуассона при постоянном значении интенсивности отказов :

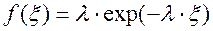(3.25)
Тогда формула для вычисления дисперсии D[T] может быть выведена на основании следующих преобразований с учетом того, что время не может быть отрицательным, т.е. в (3.24) нижний предел интегрирования равен нулю:

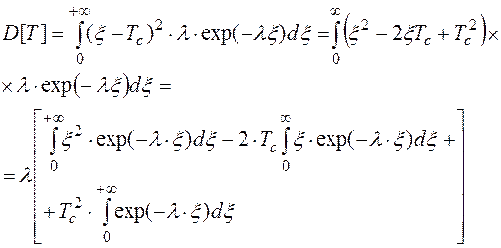(3.26)
Для вычисления этих интегралов вводятся обозначения:

,

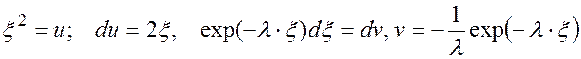тогда, пользуясь формулой интегрирования по частям, имеем:

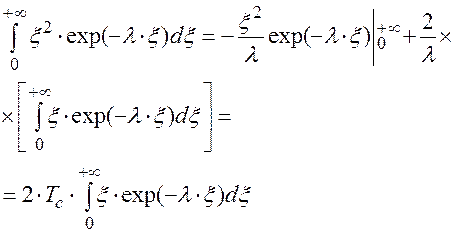
Подставляя это выражение в (3.26), получим:

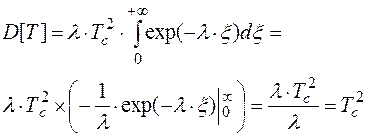(3.27)

3.6. Характеристики технических систем, используемые в теории надежности.

Коэффициент стабильности надежности K_ст –– отношение значений вероятностей исправной работы устройства для двух произвольных периодов времени;

K_ст (3.28)
Если коэффициент стабильности равен единице, то надежность системы на участке t остается неизменной.

На практике часто используется показатель изменения надежности:

(3.29)
P(t) –– вероятность нахождения системы в исправном состоянии в течение времени T ³ t.

Коэффициент стоимости эксплуатации K_сэ –– отношение стоимости одного года эксплуатации системы С_э к стоимости изготовления системы С₀:

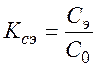(3.30)
В корректной постановке С_э=С_э(t) и чем больше срок эксплуатации системы, тем выше износ ее элементов и тем выше значение стоимости эксплуатации. Однако зачастую в инженерной практике принимают С_э=const

Особого внимания заслуживает коэффициент эффективности системы.

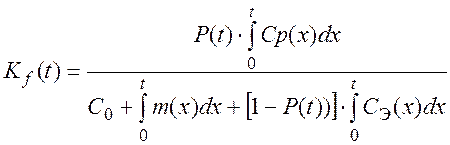(3.31)
где С₀ –– стоимость разработки (создания) системы; P(t) –– надежность технической системы; Cp(x) –– мгновенное значение прибыли; m(x) –– мгновенное значение платы за аренду (за загрязнение окружающей среды); Cэ(х) –– мгновенное значение расходов на эксплуатацию (ремонт) системы.

Для расчетного примера приняты следующие значения величин:

l=0.05 1/год; стоимость С₀=150 ед.; польза Ср(х)=40 ед.; амортизация m(x)=3 ед.; эксплуатация ,

где С_Э=1ед., К_Э=0.5 ед., что после интегрирования приводит к выражению:

Результаты расчетов по программе KFT-1.bas

T= 0 KF= 0 PT= 1

T= 4 KF= .8014488 PT= .8187308

T= 6 KF= 1.034375 PT= .7408182

T= 8 KF= 1.179153 PT= .6703201

T= 12 KF= 1.26858 PT= .5488116

T= 16 KF= 1.188045 PT= .449329

T= 18 KF= 1.114103 PT= .4065697

T= 20 KF= 1.029557 PT= .3678795

T= 22 KF= .9406778 PT= .3328711

T= 24 KF= .8519356 PT= .3011942

T= 28 KF= .685736 PT= .246597

T= 34 KF= .4814978 PT= .1826835

T= 36 KF= .4262016 PT= .1652989

Рис. 3.5. Изменение коэффициента эффективности системы и ее надежности.

Как видно из графиков рис. 3.5. срок рентабельности технической системы находится в пределах от 6 лет до 20 лет, т.е. определяется тем временем, в пределах которого числитель (3.31) превышает знаменатель или «прибыль» системы выше расходов на ее создание и эксплуатацию.

Вопросы для самоконтроля.

Дайте определение технической системы, устройства и элемента. Что называется надежностью технической системы.

Назовите основные причины недостаточной надежности систем.

Что такое цена надежности? Как изменяется стоимость технической системы в зависимости от ее надежности?

Дайте определение основных понятий теории надежности.

Назовите основные количественные характеристики надежности технической системы.

Напишите выражения для плотности распределения времени безотказной работы системы, частоты отказов, интенсивности отказов и частости отказов технической системы.

Сделайте вывод среднего значения времени наработки системы на отказ.