Задача 2.34.
В партии выпущенных изделий оказались смешанными а исправных и в неисправных изделий. Со склада без дополнительной проверки выбирается (берется сразу) k £ (a + b) изделий.
Определить математическое ожидание и дисперсию числа исправных изделий в составе выбранной партии.
Решение.
Пусть Х –– число выбранных исправных изделий
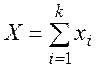 ,
,
где xi –– число исправных изделий, появившихся при i-м изъятии со склада.
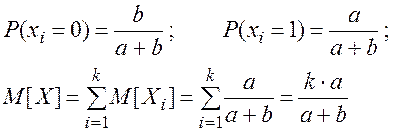
Для нахождения дисперсии D[X] найдем выражения для D[Xi ] и Kxi,
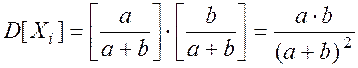
Напомним основные соотношения:
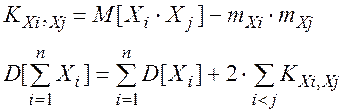
Построим таблицу распределения вероятностей для пары случайных величин Xi , Xj .
| Xj Xi | ||
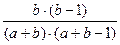
| 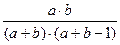
| |
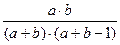
| 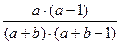
|
Имеем:
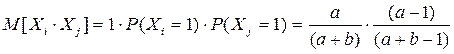
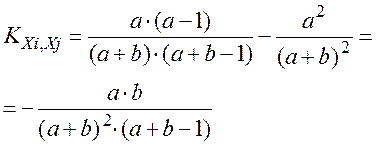
Далее можно найти дисперсию случайной величины Х:
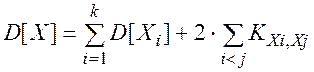
Поскольку дисперсии D[Xi] и корреляционные моменты KXi,Xj все одинаковы, то:
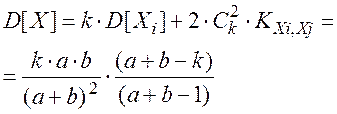
В частном случае, когда выбираются все изделия (k = a + b), получим естественный результат:
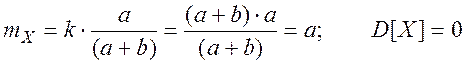 .
.
Дата добавления: 2015-05-26; просмотров: 652;
