Задача 2.31.
Автомашина проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время осмотра распределено по закону Пуассона с параметром а. Если неисправность не обнаружена, осмотр машины продолжается в среднем 2 часа. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится еще полчаса. Если обнаружено более двух неисправностей, машина ставится на ремонт, где она находится в среднем 4 часа.
Определить закон распределения среднего времени Т обслуживания и ремонта машины, определить его математическое ожидание.
Решение.
| Индекс i | ||||
| Число неисправностей | Более 2 х | |||
| Ti | 2.5 | |||
| pi | exp(-a) | 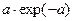
| 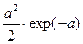
| 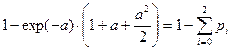
|
Математическое ожидание времени ремонта и обслуживания:
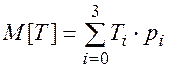
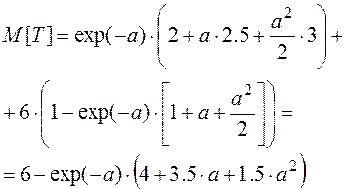
Числовые характеристики функций случайных величин.
Если Х –– дискретная случайная величина с рядом распределения
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
и величина Y связана с Х функциональной зависимостью 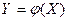 , то математическое ожидание случайной величины Y равно:
, то математическое ожидание случайной величины Y равно:
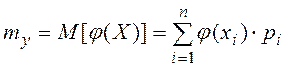 , (2.59)
, (2.59)
при этом дисперсия выражается любой из двух следующих формул:
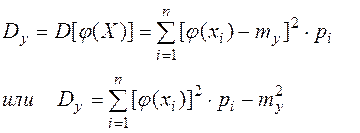 (2.60)
(2.60)
Если Х –– непрерывная случайная величина с плотностью распределения f(x), a Y=j(X), то математическое ожидание величины Y равно:
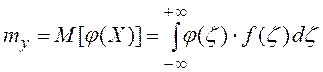 (2.61)
(2.61)
Дисперсия определяется с помощью одной из следующих двух формул:
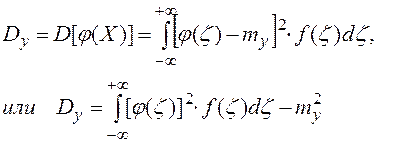
Теорема сложения математических ожиданий.
Математическое ожидание суммы случайных величин определяется по формуле:
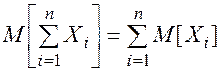 (2.62)
(2.62)
Математическое ожидание линейной функции нескольких случайных величин:
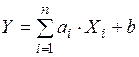 , где ai и b –– не случайные коэффициенты, равно той же линейной функции от их (случайных величин линейной функции) математических ожиданий:
, где ai и b –– не случайные коэффициенты, равно той же линейной функции от их (случайных величин линейной функции) математических ожиданий:
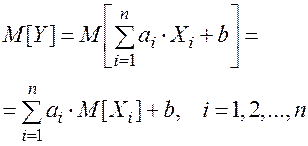 (2.63)
(2.63)
Теорема умножения математических ожиданий.
Математическое ожидание произведения двух коррелированных случайных величин X, Y выражается формулой:
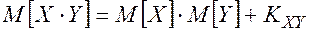 , (2.64)
, (2.64)
где КXY –– корреляционный момент величин X, Y.
Эту формулу можно записать в ином виде:
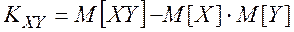 (2.65)
(2.65)
Математическое ожидание произведения двух некоррелированных случайных величин Х, Y равно произведению их математических ожиданий:
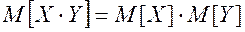 (2.66)
(2.66)
Если X1, X2, …, Xn –– независимые случайные величины, то математическое ожидание их произведения равно произведению их математических ожиданий:
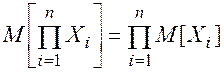 (2.67)
(2.67)
Дисперсия суммы двух случайных величин выражается формулой:
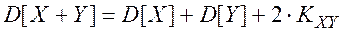 (2.68)
(2.68)
Дисперсия суммы нескольких случайных величин выражается формулой:
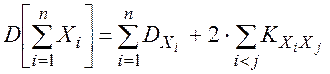 (2.69)
(2.69)
где Кxy –– корреляционный момент случайных величин Xi, Xj (2.65).
Дисперсия суммы некоррелированных случайных величин Xi равна сумме их дисперсий:
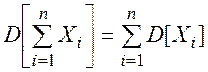 (2.70)
(2.70)
Дисперсия линейной функции нескольких случайных величин
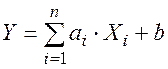
где аi , b –– не случайные величины, выражается формулой:
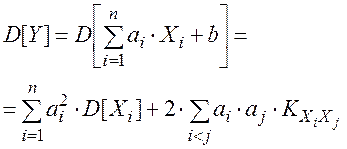 (2.71)
(2.71)
В случае, когда Х1 , Х2 , …, Хn не коррелированны,
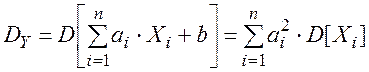 (2.72)
(2.72)
При сложении некоррелированных случайных векторов их корреляционные моменты складываются, т.е. если
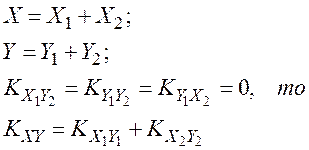 (2.73)
(2.73)
Задача 2.32.
Тело взвешивается на аналитических весах. Истинное (неизвестное нам) значение веса равно а. Вследствие ошибок результат каждого взвешивания случаен и взвешенное значение распределено по нормальному закону с параметрами а, s.
Для уменьшения ошибок пользуются следующим приемом: взвешивают тело n раз и в качестве приближенного значения веса берут среднее арифметическое:
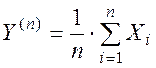
а) Найти характеристики случайной величины Y(n) (математическое ожидание и среднее квадратическое отклонение).
б) Сколько нужно сделать взвешиваний, чтобы уменьшить среднюю квадратическую ошибку веса в десять раз.
Решение.
а) 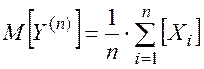
Поскольку все взвешивания производятся в одинаковых условиях, то
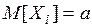 при любом i,
при любом i,
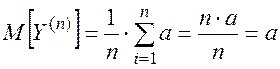
Считая ошибки отдельных взвешиваний независимыми, находим дисперсию величины Y(n) :
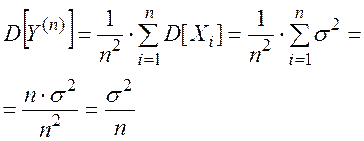
Число взвешиваний n находим из условия:
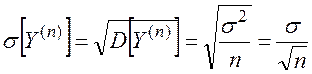
Для уменьшения среднеквадратической ошибки в десять раз необходимо выбрать значение n = 100 ( 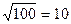 ).
).
Дата добавления: 2015-05-26; просмотров: 2128;
