Аналитический метод расчета переходного процесса
Приведем алгоритм расчета токов при возникновении однократной продольной несимметрии, используя правило эквивалентности прямой последовательности. Расчет ведем в относительных единицах.
1. Приводим полную информацию об исследуемой схеме электрической системы, выписывая из справочника данные об элементах системы, входящих в схему. Предварительно задаемся видом продольной несимметрии, которой необходим для определения Х(н).
2. Bыбираем базисные условия. За базисную мощность Sб источника питания при одном источнике питания принимаем номинальную мощность источника питания Sн; при двух или более источниках – кратную 10. За базисное напряжение принимаем среднее напряжение Uср.н той ступени напряжения, на которой возникла несимметрия.
3. Составляем схемы замещения трех последовательностей: прямой, обратной и нулевой.
4. Определяем результирующие сопротивления схем отдельных последовательностей относительно точки, где возникла та или иная несимметрия. На этом же этапе из схемы прямой последовательности находим также результирующую ЭДС относительно той же точки (рис. 11.3).
5. По сопротивлению обратной и нулевой последовательностей определяем дополнительное сопротивление Хон и удаляем действительную точку несимметрии за сопротивление Х(н), что позволяет в общем случае по выражению (11.25) определить ток прямой последовательности IнА1.
6. Модуль фазного тока при любом виде однократной продольной несимметрии определяем по выражению:
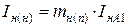, (11.27)
где mн(n) – коэффициент, определяемый из табл. 11.2.
Таблица 11.2
| Вид разрыва | Z(н) | m |
| Разрыв одной фазы | Хн2 || Xн0 |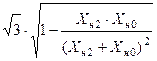 
|
| Разрыв двух фаз | Хн2 + Xн0 |
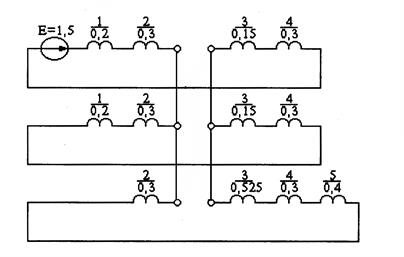
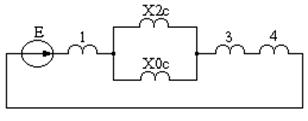
Пример 11.1. Для схемы рис. 11.16 а определить токи в линии при разрыве одной фазы. Комплексная схема, где все элементы выражены в относительных единицах при базисных условиях, приведена на рис.11.16 б).
а
б
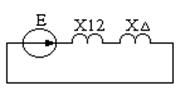
в г
Рис. 11.16. К примеру 11.1:
а – расчётная схема; б – комплексная схема;
в, г – преобразованные комплексные схемы замещения
Результирующие реактивности относительно места разрыва составляют:
,
,
.
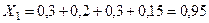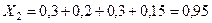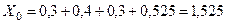Дополнительная реактивность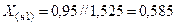 
.
Ток прямой последовательности: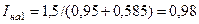 
.
Модуль тока в неповрежденных фазах:
,
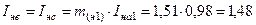где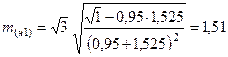 
.
Для сравнения отметим, что при нормальной работе линии фазный ток составляет I = 1,58. Следовательно, при разрыве одной фазы ток в «здоровых» фазах снижается на: 100 % (1,58 – 1,48) / 1,58 = 6,35 %.
Пример 11.2. Для схемы рис. 11.17 а определить ток в неповрежденной фазе А при разрыве фаз B и С линии.
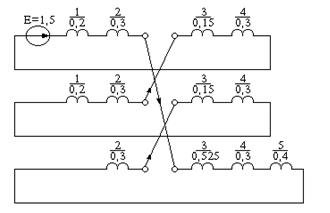
Комплексная схема показана на рис. 11.17 б, где все реактивности приведены в относительных единицах при базисных условиях.
В примере 11.1 были найдены реактивности:
; 
; 
.
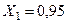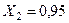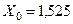Дополнительная реактивность
.
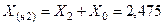Находим величину тока прямой последовательности:
.
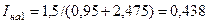Абсолютное значение тока: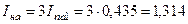 
,
т. е. на 16,8 % меньше, чем при нормальной работе линии.
а
б
в
Рис. 11.17. К примеру 11.2:
а – расчётная схема; б – комплексная схема замещения;
в – преобразованная комплексная схема замещения
Пример 11.3. Для схемы (рис. 11.18) требуется сравнить величины начальных сверхпереходных токов при несинхронном включении генератора в систему, считая, что такое включение производится одновременно: а) тремя фазами выключателя B;
б) двумя фазами (разрыв одной фазы); в) одной фазой (разрыв двух фаз).
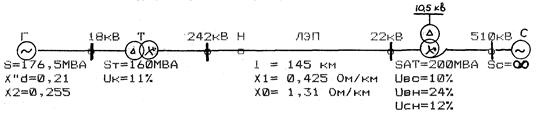
Рис. 11.18. Расчётная схема к примеру 11.3
1. Задаемся базисными условиями:
Sб = 176,5 МВ·А; Uб1 = 18 кВ; Uб2= 242 кВ; Uб3 = 577,5 кВ.
2. Сопротивления элементов приведем к базисным условиям и составим схемы замещения (рис. 11.19).
3. Результирующие реактивности схем отдельных последовательностей относительно места разрыва:
;
;
.
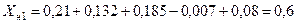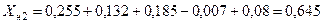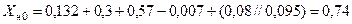4. Считаем, что при включении выключателя напряжение генератора по величине равно напряжению системы, которое в относительных единицах составляет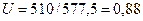 
. Наиболее тяжелые условия по току имеют место, когда напряжения включаемых источников находятся в противофазе:
а) при включении трех фаз.
Наибольшая величина сверхпереходного тока при этом будет:
;
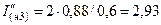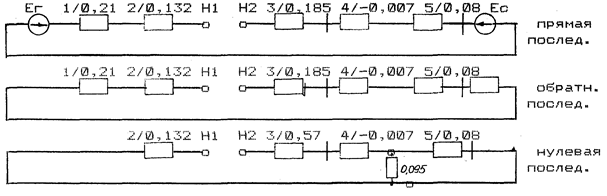Рис. 11.19. Схемы замещения к примеру 11.3
б) при включении двух фаз (разрыв одной фазы).
Дополнительная реактивность, вводимая в схему прямой последовательности будет: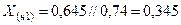 
.
Значение составляющих прямой и обратной последовательностей наибольшего сверхпереходного тока будет:
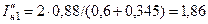и 
.
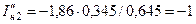Поскольку обмотки трансформатора имеют соединение Y/D, то в одной из фаз генератора эти составляющие тока будут:
.
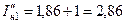в) при включении одной фазы (разрыв двух фаз).
В данном случае дополнительная реактивность составляет:
.
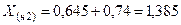Составляющие прямой и обратной последовательностей сверхпереходного тока будут:
.
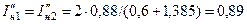В двух фазах генератора эти составляющие тока сдвинуты друг относительно друга на 60 эл. град. (имея в виду переход через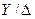 
) и, следовательно, величина сверхпереходного тока в этих фазах генератора будет:
.
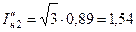Искомое соотношение между наибольшими сверхпереходными токами генератора при различных условиях его несинхронного включения получается следующим:
.
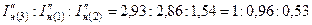Пример 11.4. От шин 10,5 кВ тепловой электростанции отходит линия к потребителю. Ее присоединение выполнено через реактор РБА-10-1000-6.
Определить для t = 0,2 c величину наибольшего тока в фазе при трехфазном КЗ за реактором при условии, что одна фаза реактора закорочена. Сравнить этот ток с током для тех же условий, но при наличии всех трех фаз реактора. Суммарная мощность станции 375 МВА, ее относительная реактивность для t = 0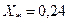 
.
Для решения воспользуемся методом расчетных кривых.
Реактивность реактора, отнесенная к номинальным параметрам станции:
,
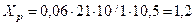где суммарный ток генераторов станции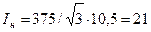 
кА.
Закорачивание фазы реактора эквивалентно включению в эту фазу реактивности Х = – 1,2. Следовательно, дополнительная реактивность, включенная в схему прямой последовательности, будет:
.
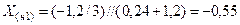При этом принято Хн0 = ∞, так как на стороне генераторного напряжения сопротивление нулевой последовательности очень велико.
Расчетная реактивность составляет:
.
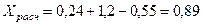По расчетным кривым при Храсч = 0,89 для t = 0,2 c находим I" = 1,0.
Ток обратной последовательности в месте несимметрии будет:
.
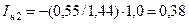Следовательно, искомый наибольший ток составит:
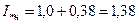или 
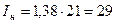кА.
При наличии трех фаз реактора Храсч = 1,44 и ток КЗ по расчетным кривым составит: I*н = 0,64 или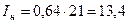 
кА.
Таким образом, закорачивание одной фазы реактора приводит к увеличению тока КЗ более чем в два раза.
Пример 11.5. Построить векторные диаграммы токов в обеих цепях линии при разрыве провода фазы А цепи 1 (рис. 11.20). Предшествующие фазные токи каждой линии составляют 305 А.
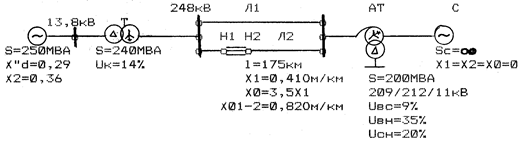
Рис. 11.20. Расчётная схема к примеру 11.5
1. Составляем комплексную схему замещения (рис. 11.21) и приводим сопротивления к напряжению разрыва.
2. Результирующие реактивности схем отдельных последовательностей:
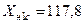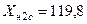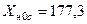Ом; 
; 
Ом.
3. Результирующая реактивность комплексной схемы относительно источника будет:
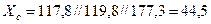Ом.
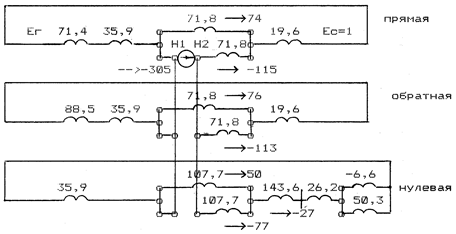
Рис. 11.21. Комплексная схема замещения к примеру 11.5
4. Аварийная составляющая тока прямой последовательности в месте разрыв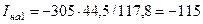а:
А.
5. Составляющие токов обратной и нулевой последовательности в месте разрыв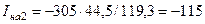а:
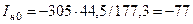А;
А.
6. Построим векторные диаграммы токов, приняв, что предшествующий ток совпадает по фазе с аварийной составляющей тока прямой последовательности.
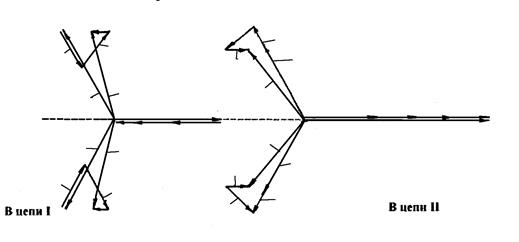
Рис. 11.22. Векторные диаграммы токов к примеру 11.5
Пример 11.6. Для заданной системы электроснабжения построить векторные диаграммы напряжений при разрыве одной и двух фаз.
Суммарное сопротивление прямой последовательности:
.
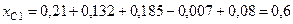Суммарное сопротивление обратной последовательности:
.
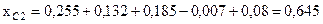Суммарное сопротивление нулевой последовательности:
.
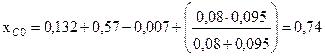Суммарная ЭДС:
.
.
.
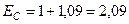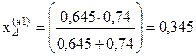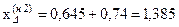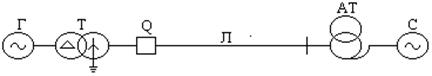
а
1. Разрав одной фазы
б
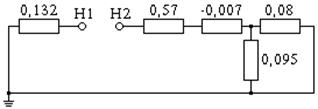
в
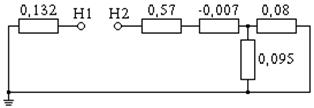
г
Рис. 11.23. Расчетная схема (а) и схемы замещения прямой (б), обратной (в)
и нулевой (г) последовательностей при разрыве одной фазы
Значения составляющих токов прямой, обратной и нулевой последовательностей:
;
;
.
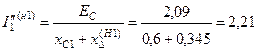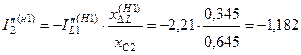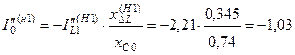Проверка:
;
.
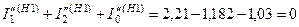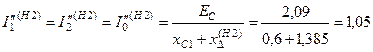Падения напряжений прямой, обратной и нулевой последовательностей:
.
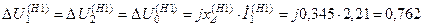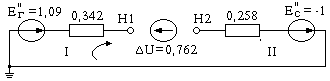
а
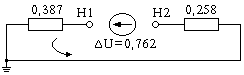
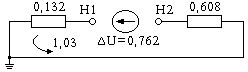
б в
Рис. 11.24. Схема замещения прямой (а), обратной (б) и нулевой (в)
последовательностей
Прямая последовательность:
.
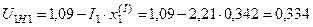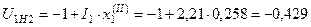
или
.
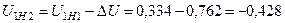Обратная последовательность:
;
.
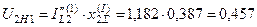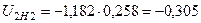Нулевая последовательность:
;
.
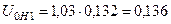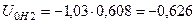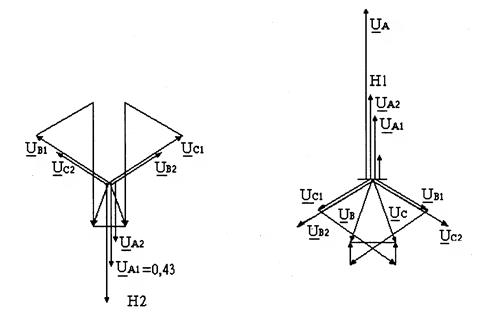
Рис. 11.25. Векторные диаграммы напряжений при разрыве одной фазы
2. Разрыв двух фаз
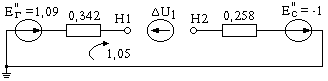
а
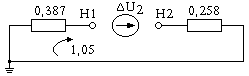
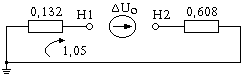
б в
Рис. 11.26. Схема замещения прямой (а), обратной (б) и нулевой (в)
последовательностей к примеру 11.6
Прямая последовательность:
;
;
;
.
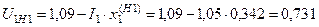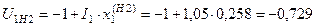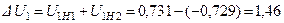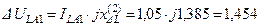Обратная последовательность:
;
;
.
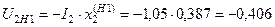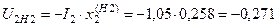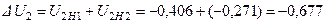Нулевая последовательность:
;
;
;
.
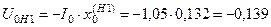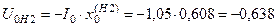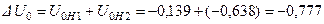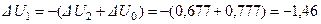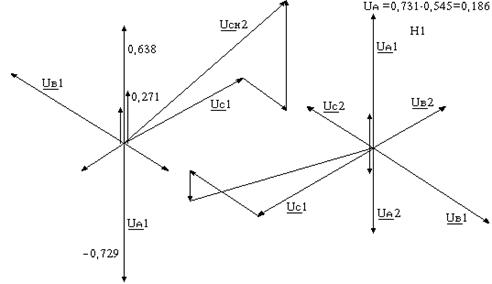
Рис. 11.27. Векторные диаграммы напряжений при разрыве двух фаз
Контрольные вопросы
1. Какие виды повреждений относят к продольной несимметрии?
2. Какой вид имеют комплексные схемы замещения при продольной несимметрии?
3. Как формулируется правило эквивалентности прямой последовательности при продольной несимметрии?
4. Какова последовательность расчёта токов в неповреждённых фазах при продольной несимметрии?
Дата добавления: 2015-05-19; просмотров: 1865;