Однофазное КЗ с разрывом фазы
Рассмотрим случай, когда одновременно возникают поперечная и продольная несимметрии.
Пусть на каком-либо участке сети, нейтраль которой заземлена, произошел разрыв одного провода, причем один конец провода заземлился, а другой остался изолированным (рис. 12.6). Питание данного участка предполагается с обеих его сторон.
Граничные условия будут:
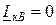 ;
; 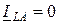 ;
;
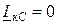 ;
; 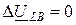 ; (12.12)
; (12.12)
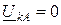 ;
; 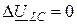 .
.
Основные уравнения:
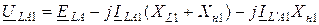 ;
;
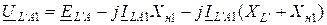 ;
;
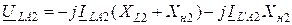 ;
;
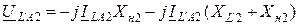 ; (12.13)
; (12.13)
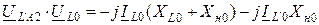 ;
;
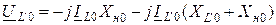 .
.
Используя (12.12) и (12.13), получим дополнительную связь между неизвестными токами и напряжениями прямой последовательности в местах несимметрии:
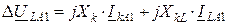 ; (12.14)
; (12.14)
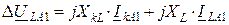 ;
;
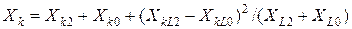 ;
;
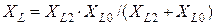 ;
;
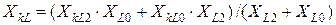 ,
,
где Хk2, Хk0 – реактивности схемы соответствующей последовательности относительно точки КЗ при полном разрыве схемы в точке L;
XL2, XL0 – то же относительно места разрыва при отсутствии КЗ;
XkL2, XkL0 – взаимные реактивности между точкой КЗ и местом разрыва в схемах соответствующих последовательностей.
Придадим уравнениям (12.14) несколько иной вид, введя в правую часть каждого уравнения два одинаковых, но противоположных по знаку, слагаемых:
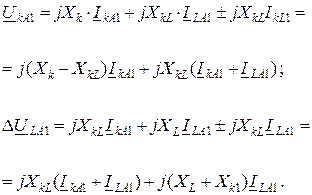 (12.15)
(12.15)

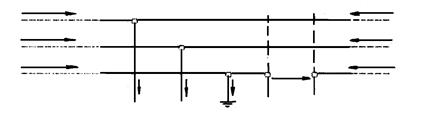
Рис. 12.6. Однофазное КЗ с одновременным разрывом той же фазы
Уравнениям (12.15) соответствует схема замещения, представленная на рис. 12.7, из которой следует, что при рассматриваемой двукратной несимметрии расчет токов и напряжений прямой последовательности (при ранее принятых допущениях) сводится к расчету эквивалентного КЗ в некоторой точке С, связанной с точками K1 и L1 схемы прямой последовательности реактивными сопротивлениями XkL, (Xk – XkL) и (XL – XkL), величины которых определяются реактивными сопротивлениями только схем обратной и нулевой последовательностей.
Таким образом, в данном случае соблюдается правило эквивалентности прямой последовательности со всеми вытекающими из него следствиями.
Нужно отметить, что на схеме рис. 12.7 за положительное направление тока ILA1 принято направление от места замыкания. Чтобы увязать с обычно принимаемым условием, что токи имеют положительное направление к точке КЗ, необходимо у найденного тока ILA1 изменить знак.
Напряжение прямой последовательности в месте КЗ относительно нулевого провода и относительно оборванного конца фазы (ΔULA1) определяются суммой соответствующих падений напряжений в схеме (рис. 12.7).

|
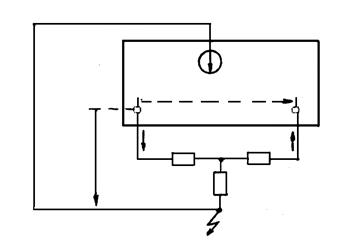
Рис. 12.7. Схема прямой последовательности для случая однофазного КЗ с одновременным разрывом той же фазы
Остальные симметричные составляющие токов и напряжений в обоих местах несимметрии определяются из соотношений, которые вытекают из граничных условий и уравнений связи (12.2) и (12.3).
Распределение токов и напряжений находят обычными приемами или с использованием принципа наложения.
Если приведенные ЭДС источников равны между собой, и параметры прямой и обратной последовательностей принять одинаковыми, то для определения тока прямой последовательности в месте КЗ при одновременном разрыве той же фазы с одной стороны можно получить простое расчетное выражение:
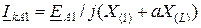 , (12.16)
, (12.16)
где Х(1) = 2Х1 + Х0– результирующая реактивность при однофазном КЗ в точке К и отсутствии разрыва фазы в точке L;
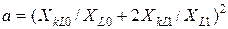 ; (12.17)
; (12.17)
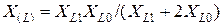 , (12.18)
, (12.18)
где ХL1 и XkL1 – то же, что ранее XL2 и XkL2.
Из структуры выражения (12.16) непосредственно видно уменьшение тока КЗ, вызванное одновременным разрывом поврежденной фазы с одной стороны.
Пример 12.1. При двойном замыкании на землю в точках M и N схемы
(рис. 12.8 а) определить фазные токи линии и обоих трансформаторов (на стороне, где произошло замыкание), а также фазные напряжения в местах замыкания. Расчет произвести для начального момента, считая, что генератор предварительно работал на холостом ходу с номинальным напряжением.
Генератор Г37,5 МВ·А; 6,3 кВ; Х"d* = 0,143 = X1 = X2;
Трансформатор Т-1 25 МВ·А; 37/6,3 кВ; Uк = 8 %; У/Д – 11;
Трансформатор Т-2 40 МВ·А; 115/37/10,5 кВ; Uвc = 10,5 %; У/Д/Уо;
Линия Л 12,5 км; X1 = 0,4 Ом/км; X0 = 1,45 Ом/км.
Система С – источник бесконечной мощности с напряжением 115 кВ.


а

б

в


г
Рис. 12.8. К примеру 12.1:
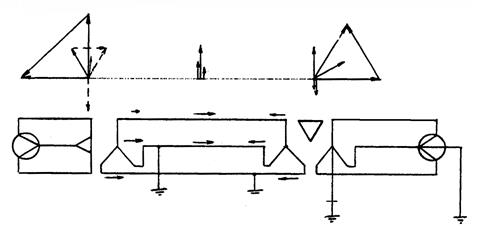
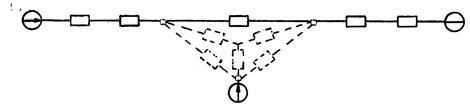
а – расчётная схема; б – распределение токов, векторная диаграмма
токов и напряжений; в – схема замещения прямой (обратной)
последовательности; г – то же нулевой последовательности
На рис. 12.8 в показана схема замещения прямой последовательности, где указаны реактивные сопротивления (Ом) всех элементов и ЭДС (кВ) источников. После исключения ЭДС получившаяся схема является схемой замещения обратной последовательности. Схема нулевой последовательности (рис. 12.8 г) содержит только один элемент – линии.
Объединив начала генерирующих ветвей, получим треугольник, преобразование которого в звезду (пунктир на рис.12.8 в) дает реактивные сопротивления схем прямой (обратной) последовательностей.
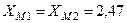 Ом;
Ом; 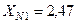 Ом;
Ом; 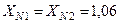 Ом;
Ом; 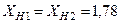 Ом.
Ом.
По (12.10) находим: 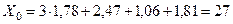 Ом.
Ом.
Принимая 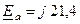 кВ, для тока прямой последовательности по (12.9) имеем:
кВ, для тока прямой последовательности по (12.9) имеем:
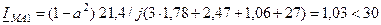 град.
град.
и для токов других последовательностей:
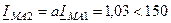 град., кА,
град., кА, 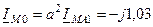 кА.
кА.
С – источник бесконечной мощности (X1 = X2 = X0 = 0) с напряжением 115 кВ.
Найдем распределение токов, для чего предварительно определим необходимые коэффициенты распределения:
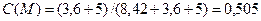 ,
, 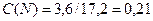
и со стороны трансформатора Т-2:
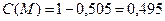 ;
;
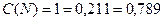 .
.
Эти коэффициенты справедливы и для схемы обратной последовательности. Поскольку при отсутствии замыканий тока в линии нет (пренебрегая емкостным током), фазные токи трансформатора Т-1 с учетом того, что здесь 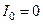 , будут:
, будут:
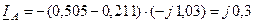 кА;
кА;
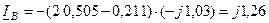 кА;
кА;
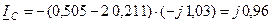 кА;
кА;
Для фазных токов линии имеем:
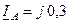 кA;
кA; 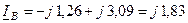 кА;
кА; 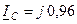 кА.
кА.
Аналогично для фазных токов трансформатора Т-2 (учитывая принятое положительное направление токов, указанное стрелками на рис. 12.7 а):
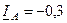 кA;
кA; 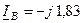 кА;
кА; 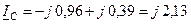 кА.
кА.
Для симметричных составляющих напряжений в точке M имеем:
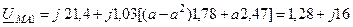 кВ,
кВ,
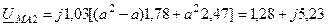 кВ,
кВ,
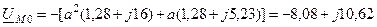 кВ.
кВ.
Аналогично для симметричных составляющих напряжений в точке N получаем:
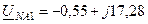 кB;
кB; 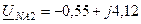 кВ;
кВ; 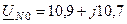 кВ.
кВ.
Контрольные вопросы
1. Какие виды повреждений называют сложными?
2. Какие сложные виды повреждений наиболее часто имеют место в трёхфазных СЭС?
3. Каковы граничные условия для двойного замыкания на землю?
4. Каковы граничные условия для однофазного КЗ с одновременным разрывом той же фазы?
5. Какова последовательность действий при анализе сложных видов повреждений?
13. Электромагнитные переходные процессы
в особых условиях
13.1.Особенности расчетов токов КЗ в распределительных сетях напряжением 6 – 35 кВ
Распределительными сетями называют воздушные и кабельные сети напряжением 6 – 35 кВ, по которым электроэнергия передается потребителям от питающих центров, понижающие трансформаторы, а также воздушные и кабельные линии.
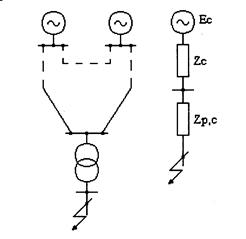
Основной особенностью распределительных сетей является их значительная электрическая удаленность от генераторов энергосистемы (рис. 13.1). Путем преобразования схемы генераторы и сети СЭС (рис. 13.1 а) приводят к простейшей схеме замещения (рис. 13.1 б), в которой все генераторы заменяются одним эквивалентным генератором с электродвижущей силой Ес, а сопротивления всех линий, трансформаторов и генераторов до шин питающей подстанции заменяются сопротивлением системы Zc. Сопротивления линий и трансформаторов распределительной сети от шин питающей подстанции до места КЗ суммируются и заменяются одним сопротивлением Zрс. Таким образом, вся расчетная схема приводится к схеме на рис. 13.1 б, а суммарное сопротивление от эквивалентного источника питания до точки КЗ составляет
Zк = Zс + Zрс.
Ток трехфазного КЗ I(3)k через сопротивление Zк = Zc + Zpc определяется как для источника с неизменной фазной электродвижущей силой Ес:
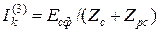 , (13.1)
, (13.1)
где величины Zc и Zp определены для одной фазы, Ом/фазу.
При значительной электрической удаленности распределительной сети обычно не учитывают переходные процессы в генераторах, считая все КЗ удаленными, что упрощает расчеты. В практических расчетах фазная ЭДС генераторов Ес заменяется линейным напряжением холостого хода Uх вторичной обмотки трансформатора, питающего распределительную сеть:
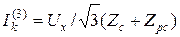 . (13.2)
. (13.2)
а б
Рис. 13.1. Расчетная схема (а) и схема замещения (б) для расчета тока КЗ
Для распределительных сетей сложной конфигурации величина Zc определяется расчетами, которые обычно выполняются с помощью ЭВМ. В результате для всех подстанций и электростанций ЭЭС определяется ток КЗ на шинах, питающих распределительную сеть 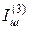 , а по нему определяется Zc для расчетов токов КЗ в самой распределительной сети:
, а по нему определяется Zc для расчетов токов КЗ в самой распределительной сети:
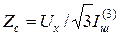 . (13.3)
. (13.3)
Иногда вместо тока трехфазного КЗ задается мощность КЗ 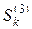 , которая равна
, которая равна 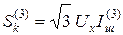 . Сопротивление системы в этом случае определяется по уравнению:
. Сопротивление системы в этом случае определяется по уравнению:
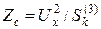 . (13.4)
. (13.4)
Таким образом, исходными данными для расчетов токов КЗ в распределительных сетях являются величины Ux и Zc. Величина Zрc определяется для каждого случая по данным рассчитываемой сети: длине, сечению и расположению проводов линий, паспортным данным трансформаторов, длине, сечению и конструкции кабелей и т. п.
Важной особенностью распределительных сетей является возможность не учитывать апериодическую составляющую тока КЗ, которая вследствие большого значения активного сопротивления затухает быстро – за сотые доли секунды.
Следующим упрощением для расчетов в распределительных сетях является возможность не вычислять ток двухфазного КЗ, а определять его по току трехфазного КЗ, предполагая, что суммарное сопротивление прямой последовательности 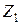 равно суммарному сопротивлению обратной последовательности
равно суммарному сопротивлению обратной последовательности 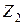 . При этом ток двухфазного КЗ I(2)к равен
. При этом ток двухфазного КЗ I(2)к равен
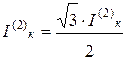 . (13.5)
. (13.5)
В ряде случаев сопротивление Zc по сравнению с Zрc настолько мало, что им можно пренебречь и принять Zc = 0. Такой случай считается питанием от системы бесконечной мощности. Для ориентировочной оценки электрическую систему можно считать системой бесконечной мощности, если выполняются условия уравнений:
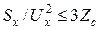 (13.6)
(13.6)
или
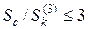 , (13.7)
, (13.7)
где Sc – суммарная мощность всех генераторов энергосистемы, МВ·A;
S(3)k – мощность трехфазного КЗ на шинах подстанции, питающей распределительную сеть, МВ·А;
Zc – сопротивление системы, приведенное к шинам питающей подстанции, Ом/фазу.
Следующая особенность расчета – необходимость учета активных сопротивлений. Считается, что пренебрегать активным сопротивлением можно, если Xc / Rc ≥ 3. При этом определение тока КЗ без учета активного сопротивления дает ошибку не более 5 %.
В распределительных сетях индуктивное сопротивление воздушных линий Xвл составляет 0,3 – 0,4 Ом/км, активное сопротивление Rвл для алюминиевых проводов сечением 16 – 70 мм² находится в пределах 2,0 – 0,5 Ом/км; отношение Xвл/Rвл при этом значительно меньше 3 и находится в пределах 0,15 – 0,6.
Для кабелей индуктивное сопротивление составляет 0,08 Ом/км и отношение Хкл/Rкл еще меньше. Поэтому одним из основных требований является обязательный учет активных сопротивлений сети. В этом случае расчетное уравнение (13.2) приводится к виду:
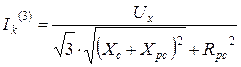 . (13.8)
. (13.8)
Распределительные сети напряжением 6 – 35 кВ работают с изолированной нейтралью или с компенсацией емкостных токов замыкания на землю. Поэтому в них возможны следующие повреждения: трехфазные, двухфазные КЗ и двойные КЗ на землю, а также однофазные замыкания на землю.
При однофазных замыканиях на землю треугольник линейных напряжений не изменяется, все потребители могут продолжать нормально работать и быстрого отключения однофазного замыкания не требуется. Исключением являются сети, питающие передвижные приемники энергии: например, экскаваторы, машины для добычи торфа, передвижные подстанции, шахты и карьеры для добычи полезных ископаемых и некоторые другие потребители, у которых при замыкании на землю возникает повышенная опасность для персонала. В таких сетях [1] требуют немедленного автоматического отключения поврежденной линии.
Немедленное отключение требуется и при замыкании на землю в обмотках генераторов и двигателей при токе замыкания на землю более
5 или 10 А. Для сетей непосредственно связанных с генераторами и двигателями 6 – 10 кВ, работа с замыканием на землю в сети допускается не более 2 ч и лишь в особых случаях до 6 ч. Для всех остальных сетей допускается работа с замыканием на землю до устранения повреждения персоналом в минимально возможный срок.
Все расчеты токов выполняются обычно для металлического КЗ, т. е. когда токоведущие части фаз соприкасаются между собой непосредственно, без переходного сопротивления. Принято это вследствие трудности определения значения переходного сопротивления, которым может быть дерево, упавшее на линию, часть деревянной опоры и т. п.
Расчет токов КЗ может выполняться в именованных и в относительных единицах. Точность расчетов при этом одинаковая. Для распределительных сетей обычно приходится определять активные и индуктивные сопротивления линий и трансформаторов по справочникам или расчетным уравнениям. Большинство данных в справочниках приводятся в именованных единицах, поэтому для уменьшения пересчетов расчеты для распределительных сетей целесообразно проводить в именованных единицах. Вторым преимуществом расчета в именованных единицах является то, что после каждого вычисления появляется результат в именованных единицах, что позволяет непрерывно контролировать правильность ведения расчетов и получаемых результатов.
Ток замыкания на землю рассчитывается по формуле:
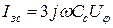 , (13.9)
, (13.9)
где Cc – суммарная ёмкость одной фазы относительно земли, ф .
Суммарная ёмкость складывается из ёмкости воздушных и кабельных ЛЭП Сл ; двигателей Сдв и других электрически связанных элементов СЭС:
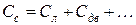 ,
,
где 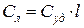 ;
;
Суд – емкость одной фазы сети относительно земли, ф/км ;
l – общая протяжённость одной фазы сети.
Ток замыкания Iзкл на землю для сети с КЛ можно определить по имперической формуле
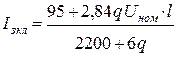 , (13.10)
, (13.10)
где Uном – номинальное линейное напряжение сети, кВ;
l – длина КЛ, км;
q – сечение кабеля, мм2 .
Для двигателей неянополюсных синхронных и короткозамкнутых асинхронных
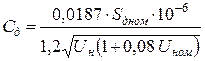 , Ф, (13.11)
, Ф, (13.11)
где Sдном – номинальная мощность двигателя, МВА;
Uн – номинальное линейное напряжение, кВ.
Для остальных двигателей
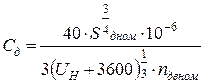 , Ф, (13.12)
, Ф, (13.12)
где Sдном – мощность двигателя, кВА;
Uн – линейное напряжение, В;
n – частота вращения ротора, об/мин.
Пример 13.1. От шин подстанции с вторичным напряжением 11 кВ питаются три линии. Первая линия выполнена алюминиевым кабелем 3×50 мм², вторая – алюминиевым проводом А50. Длина каждой линии 5 км . Ток КЗ на шинах 11кВ 3000 А. Определить ток КЗ в конце каждой линии.
Решение. Сопротивление энергосистемы, приведенное к шинам 11 кВ, равно:
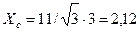 Ом.
Ом.
Сопротивление кабеля 11 кВ A-50 по [17] равно: 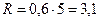 Ом;
Ом; 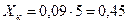 Ом. Ток КЗ в конце кабельной линии равен:
Ом. Ток КЗ в конце кабельной линии равен:
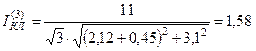 кА.
кА.
Этот ток без учёта активного сопротивления КЛ равен:
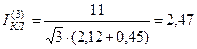 кА,
кА,
то есть ошибка составила 56,4 %, что недопустимо.
Ток двухфазного КЗ в конце КЛ равен 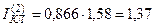 кА.
кА.
Удельные индуктивное и активное сопротивления ВЛ выполнены проводом А50 по [17] равны 0,364 Ом/км и 0,576 Ом/км. Индуктивное и активное сопротивления ВЛ равны:
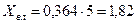 Ом;
Ом;
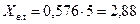 Ом.
Ом.
Ток трёхфазного КЗ в конце линии
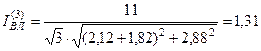 кА.
кА.
Без учёта активного сопротивления этот ток равен
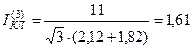 кА.
кА.
Ток двухфазного КЗ в конце КЛ 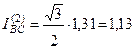 кА.
кА.
Если КЗ сопровождается дугой длиной 1200 мм (примерно среднее расстояние между проводами, что справедливо для первого момента КЗ), то
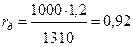 Ом,
Ом,
и ток 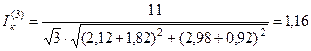 кА,
кА,
или 0,885 тока, определенного без учета дуги.
Такое незначительное уменьшение тока объясняется тем, что сопротивление дуги мало по сравнению с активным сопротивлением линии.
Дата добавления: 2015-05-19; просмотров: 2871;