Нагрев проводов током КЗ
При КЗ активное сопротивление проводов увеличивается за счет нагрева их током КЗ, что вызывает уменьшение тока. Уменьшение тока вызывает увеличение времени работы зависимых максимальных защит: при малой чувствительности в принципе возможен возврат защиты.
Подробный анализ и обоснование метода учета этого явления рекомендуется выполнять расчет с помощью диаграммы, приведенной на
рис. 13.2.
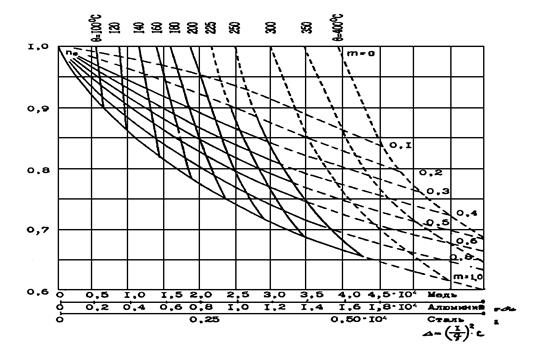
Рис. 13.2. Диаграмма для учёта теплового спада тока
короткого замыкания
На диаграмме принята начальная температура θ0= 65 °C, тепловой коэффициент a для меди и алюминия 0,0041/°C, для стали 0,0045/°C. Сплошные линии на диаграмме предназначены для медных и алюминиевых проводов, пунктирные – для стальных. Для стальных проводов расчет дает лишь ориентировочные значения. Пользование кривыми поясняется примером.
На этой диаграмме по оси абсцисс отложена величина Δ = (I(3)/q)²t,
где q – сечение провода, мм²; t – время прохождения тока, с.; I(3) – ток трехфазного КЗ в начальный момент. По оси ординат отложена величина ne – коэффициент теплового спада тока от нагрева проводов.
Кривые θ дают температуру провода, °C;
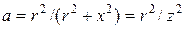 , (13.13)
, (13.13)
где r, x, z – сопротивления цепи КЗ.
Пример 13.2. Ток КЗ на шинах питающей подстанции 10 кА при напряжении 6,6 кВ. Выполнить расчет спадания тока через 1, 2, 3 с для медного кабеля сечением
50 мм², длиной 5 км.
Решение. Определим активное сопротивление кабеля при температуре 65 ºC. По приложению [17] активное сопротивление медного кабеля 50 мм2 при температуре +20 ºC равно 0,37 Ом/км. При температуре 65 ºC сопротивление будет 0,37 [1 +
+ 0,004(65-20)] = 0,436 Ом/км.
Полное активное сопротивление 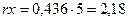 Ом.
Ом.
Сопротивление системы 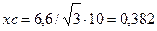 Ом.
Ом.
Сопротивление кабеля 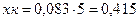 Ом.
Ом.
Ток трехфазного КЗ в конце кабеля в первый момент
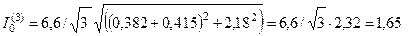 кА.
кА.
Расчет для времени t = 1 c:
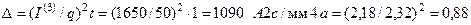 .
.
На диаграмме рис. 13.2 по шкале абсцисс для меди откладываем величину
∆ = 1,09 104 и из этой точки восстанавливаем перпендикуляр до пересечения с кривой a. На диаграмме нет кривой для a = 0,88. Поэтому точка пересечения определяется как промежуточная между кривыми для a = 1 и a = 0,8. Точка пересечения, перенесенная на ось ординат, дает ne = 0,87 и ток 0,87 1650 = 1430 А.
Температура кабеля определяется для этой же точки как промежуточная между кривыми для e = 120 °С и 140 °C, примерно 130 °C.
Для времени t = 2 c:
Δ = (1650/50)² 2 = 2180 А² с/мм4.
Аналогичным построением определяются ne = 0,78, ток 0,78· 1650 А и температура 180 ºC.
Для времени t = 3 с:
Δ = (1650/50)² 3 = 3270 А²с/мм4.
Аналогичным построением определяются nе = 0,72, ток 0,72 · 1650 = 1180 А и температура 225 °С.
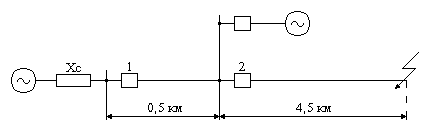
Рис. 13.3. Схема сети к примеру 13.2
Как пример практического применения подобных расчетов рассмотрим схему на рис. 13.3. Кабель медный 3х50 мм² при напряжении 6 кВ допускает длительную нагрузку 200 А. Ток срабатывания защиты должен не менее чем в 4 раза превышать ток нагрузки, т. е. должен быть не менее 800 А, отстраиваться от токов самозапуска электродвигателей и обеспечивать чувствительность при резервировании не менее 1.2. Следовательно, ток срабатывания защиты 1 (0,866 ·1650) / 1,2 = 1200 Ас кратностью к току нагрузки
1200 / 200 = 6 вполне реален. Реальна и выдержка времени 3 с и более для зависимых защит при расчетной кратности тока 1650 / 1200 = 1,2 и любых уставках по времени в независимой части. Расчет показывает, что кабель 3х50 мм² через 3 с нагреется до 225 °С при допустимых 200 °С. Это не противоречит условиям выбора выдержки времени защиты 1 по термической стойкости кабеля, так как ее время действия при КЗ в конце первого участка кабеля будет значительно меньше и кабель будет термически стоек. В данном случае при отказе защиты или выключателя 2 защита, установленная на выключателе 1, также может отказать, так как ее ток возврата 0,85 · 1200 = 1000 А, и при спадании тока двухфазного КЗ до 0,866 · 1180 = 935 А защита может вернуться, не отключив КЗ.
Отсюда следует важный вывод: при больших выдержках времени резервных защит необходимо проверять чувствительность защит с учетом нагрева проводов током КЗ.
Для трансформаторов рассчитать уменьшение тока по изложенной методике нельзя – неизвестно сечение провода обмоток, к тому же обмотки высшего и низшего напряжения имеют разные сечения и часто выбираются не по плотности тока, а по конструктивным соображениям. Но оценить уменьшение тока от нагрева можно по предельной температуре обмоток при КЗ для масляных трансформаторов с медными обмотками и изоляцией класса А 250 °С и для алюминиевых обмоток 200 °С.
Потери короткого замыкания, по которым вычисляется активное сопротивление трансформаторов, даются для температуры обмоток 75 ºС. Следовательно, увеличение сопротивления обмоток можно определить: r 250 = r75[1+0,004(250-75)] = 1,7r75. Зная r 250 и считая неизменным Хт, можно определить Zт и по нему ток КЗ. Следует учитывать, что указанной температуры обмотки достигают за время прохождения тока КЗ tк. Допустимое по термической стойкости время tк определяется по выражению, приведенному в ГОСТ: tк = 900/k², где k – кратность тока КЗ по отношению к номинальному току. Поскольку сопротивление энергосистемы невелико по сравнению с сопротивлением трансформатора, им практически можно пренебречь. Путем преобразований выражение, рекомендуемое ГОСТ, приводится к более удобному виду:
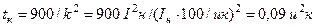 ;
; 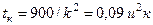 . (13.14)
. (13.14)
Для большинства трансформаторов распределительных сетей uк = 4,5 % и
tк = 0,09x 4,5² = 1,82 с.
13.3. Учёт РПН трансформаторов при расчётах токов КЗ
Полное сопротивление двухобмоточных трансформаторов выбирается по выражению:
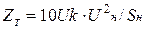 , (13.15)
, (13.15)
где Uk – напряжение короткого замыкания, %; Uн – номинальное напряжение трансформатора, кВ; Sн – номинальная мощность, MВ·А.
Активное сопротивление определяется по потерям КЗ в трансформаторе:
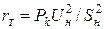 , (13.16)
, (13.16)
где Pk – потери КЗ, Вт.
В выражениях (13.15) и (13.16) в качестве Uн можно подставить номинальное напряжение любой обмотки трансформатора. Сопротивление трансформатора будет приведено к тому напряжению, которое подставляется в выражения (13.15) и (13.16).
Индуктивное сопротивление трансформатора определяется по выражению:
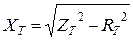 . (13.17)
. (13.17)
Все необходимые данные указываются в каталогах и на паспортах трансформаторов.
При расчетах необходимо иметь в виду, что на все данные трансформаторов имеют определенные разбросы. Например, действительная величина Uk трансформатора может отличаться от каталожной величины для этого трансформатора на 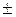 10 %; действительные потери короткого замыкания могут отличаться на
10 %; действительные потери короткого замыкания могут отличаться на 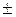 10 % .
10 % .
Поэтому при расчетах токов КЗ следует пользоваться действительными данными, указанными в технической документации. Пользоваться каталожными данными можно только при проектировании, когда действительные данные неизвестны.
Схема замещения трехобмоточного трансформатора приведена на рис. 13.4. Для таких трансформаторов указывается три величины Uк для каждой пары обмоток: высшего-среднего (ВС), высшего-низшего (ВН) и среднего-низшего (СН).
Для большинства трансформаторов 220-110/35/6-10 кВ эти величины равны примерно 17, 10, 6 %. Величины Uк относятся к наибольшей из мощностей, обычно к обмотке высшего напряжения. Сопротивления лучей эквивалентной звезды сопротивлений трехобмоточного трансформатора определяются по системе уравнений:
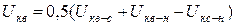 ;
;
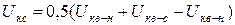 ; (13.18)
; (13.18)
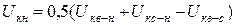 .
.
Определив Uкв, Uкс, Uкн по выражению (13.15), находят полные сопротивления лучей звезды в Омах.
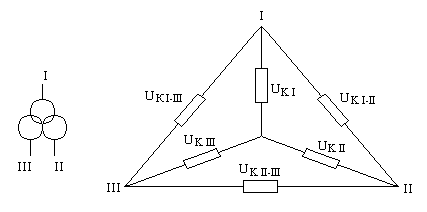
Рис. 13.4. Исходная схема и схема замещения трехобмоточного
трансформатора
Активное сопротивление большинства современных трехобмоточных трансформаторов достаточно большой мощности настолько мало, что не учитывается, а полные сопротивления считаются чисто индуктивными. Если требуется определить активные сопротивления трехобмоточного трансформатора, то следует учитывать, что указываемые в каталогах значения потерь короткого замыкания относятся к наиболее тяжелому случаю: обмотка высшего напряжения и одна из обмоток среднего или низшего напряжения загружены полностью, вторая обмотка среднего или низшего напряжения находится без нагрузки.
Трехобмоточные трансформаторы выполняются с мощностями среднего или низшего напряжения обмоток, равным 100 %, или 67 % мощности первичной обмотки. Для трансформатора с мощностью вторичной обмотки среднего или низшего напряжения, равной 100 % мощности обмотки высшего напряжения, активное сопротивление определяется по выражению:
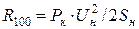 . (13.19)
. (13.19)
Сопротивление обмотки, мощность которой равна 67 % мощности обмотки высшего напряжения, определяется по величине R100:
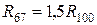 . (13.20)
. (13.20)
Для питания крупных потребителей (сети крупных городов и промышленных предприятий) применяются трансформаторы с расщепленной обмоткой низшего напряжения. У таких трансформаторов имеются две одинаковые обмотки низшего напряжения с одинаковой схемой соединений и одинаковой мощностью каждой обмотки, равной 50 % мощности обмотки высшего напряжения. При расчете сопротивлений таких трансформаторов следует учитывать, что величина Uк для них указывается для мощности каждой обмотки низшего напряжения.
Практически все современные трансформаторы имеют ответвления от обмоток для регулирования напряжения. В большинстве случаев изменение сопротивления трансформатора при регулировании напряжения, а следовательно, и изменение тока КЗ из-за этого не учитывается. Но в ряде случаев эти изменения приходится учитывать и возникает вопрос о вычислении сопротивления трансформатора при изменении числа витков его обмоток. У большинства трансформаторов распределительной сети ответвления для регулирования напряжения выполняются на стороне обмотки высшего напряжения. В соответствии с ГОСТ 11677-75 требуется, чтобы все трансформаторы допускали длительную работу при напряжении питания, превышающем номинальное напряжение данного ответвления не более чем на 5 % при номинальной нагрузке и 10 % кратковременно (до 6 ч в сутки) или длительно при нагрузке 25 % номинальной. Для трансформаторов распределительных сетей с регулированием типов ПБВ и РПН с достаточной для практики точностью сопротивление трансформаторов для любого положения переключателя ответвлений Zтр можно определить по формуле:
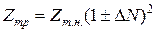 , (13.21)
, (13.21)
где Zт.н – сопротивление трансформатора, определенное по выражению (13.15) для номинального напряжения;
∆N – количество ответвлений; изменение напряжения при переводе переключателя в одно следующее положение, ОЕ.
В соответствии с ГОСТ для трансформаторов распределительных сетей предусмариваются два основных предела регулирования: для регулирования типа ПБВ – обычно ± 2х2,5 %; для регулирования типа РПН у трансформаторов 25 – 630 кВ·А, 6 – 35кВ ± 6х1,67 % = ± 10 %. Для трансформаторов большой мощности более высоких напряжений пределы регулирования доводят до ± 16 %.
Большинство трансформаторов в распределительных сетях имеют пределы регулирования типа ПБВ ± 2 х 2,5 %. Сопротивление таких трансформаторов, определенное по выражению (13.21), будет изменяться в пределах
 .
.
При неизменном напряжении питания, равном номинальному напряжению основного ответвления Uн , и питания от системы бесконечной мощности ток трехфазного КЗ на выводах низшего напряжения будет изменяться в следующих пределах:
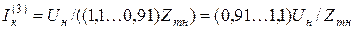 .
.
При регулировании типа РПН в пределах ±10 % сопротивление трансформатора будет изменяться в пределах:
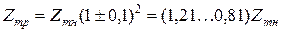 ,
,
а ток – в пределах
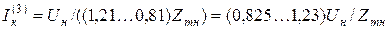 .
.
Допускается работа трансформаторов при напряжении на его вводе на 10 % превышающем номинальное напряжение.
Значение токов КЗ (за единицу принят ток КЗ при номинальном напряжении Uн) при различных напряжениях питания Uр и различных положениях переключателя ответвлений следующие:
| Положение переключателя | -10 | -5 | +5 | +10 | |
| Напряжение питания Uр,ОЕ | 1,05 | 1,1 | 1,15 | 1,2 | |
| Сопротивление трансформатора Zтр,ОЕ | 0,825 | 0,91 | 1,1 | 1,21 | |
| Ток КЗ Iк(3),ОЕ | 1,21 | 1,15 | 1,1 | 1,05 | 0,99 |
За расчетное напряжение питания Uр принимается вторичное напряжение трансформаторов, питающих распределительную сеть. Для современных трансформаторов – это 38,5; 11 и 6,6 кВ, что составляет 1,1 номинального напряжения сетевых трансформаторов 35; 10 и 6 кВ. Следовательно, расчетные условия (расчетное напряжение, равное 1,1 номинального напряжения сетевых трансформаторов, и номинальное сопротивление) соответствуют среднему значению тока КЗ 1,1. При установке переключателей ответвления при регулировании ПБВ в положения ±5 % токи КЗ отличаются всего на 5 % от расчетного, что вполне допустимо.
При регулировании типа РПН в пределах ±10 % возможные отклонения действительного тока от расчетного больше. Но трансформаторы с РПН имеют автоматическое управление, и отклонение действительного напряжения питания Uр от номинального напряжения Uр.н ответвления не превосходит одной ступени регулирования или 1,67 %. В этом случае при положении переключателя ответвлений (±10 %) ток будет равен:
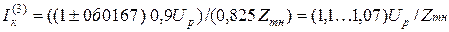 ,
,
или 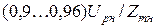 .
.
Следовательно, принятые расчетные условия обеспечивают определение расчетного тока КЗ при любых положениях ответвлений и питании от системы бесконечной мощности с точностью ±(5...10) %, что вполне достаточно. Действительные значения отклонений будут еще меньше, так как последовательно с сопротивлением трансформатора будет включено сопротивление линии распределительной сети.
Для трансформаторов с регулированием РПН в пределах ±16 % применяется автоматическое регулирование напряжения. Вопрос об учете изменения сопротивления трансформаторов решается в зависимости от местных условий, в основном от пределов действительного колебания напряжения.
13.4. Расчёт токов КЗ в сети 0,4 кВ
Расчёт токов трёхфазного и двухфазного КЗ в сетях 0,4 кВ выполняется по методике, изложенной в параграфе 13.1. При этом необходимо учитывать не только активные и индуктивные сопротивления всех элементов короткозамкнутой цепи, но и активные сопротивления всех переходных контактов в этой цепи (машинах, вводах и выводах аппаратов, разъёмные контакты аппаратов, сопротивление дуги в месте КЗ, а также сопротивления катушек расцепителей автоматов и первичных обмоток трансформатров тока).
Для расчётов рекомендуется пользоваться [17], в котором приведены сопротивления элементов аппаратов по данным заводов-изготовителей.
Испытания показали, что реально имеющие место величины токов при КЗ значительно меньше расчётных величин токов, найденных без учёта сопротивлений контактных соединений (на 60 – 80 %).
При определении сопротивления необходимо учитывать сопротивление дуги в месте КЗ, значение которого принимается 0,01 Ом.
При отсутствии достоверных данных о контактах и их переходных сопротивлениях рекомендуется при расчёте токов КЗ в сетях, питаемых трансформаторами мощностью до 1600 кВА включительно, учитывать их суммарное сопротивление введением в расчёт активного сопротивления:
1. Для распределительных устройств на станциях и подстанциях – 0,015 Ом;
2. Для первичных цеховых распределительных пунктов, как и на зажимах аппаратов, питаемых радиальными линиями от щитов подстанций или от главных магистралей – 0,02 Ом;
3. Для вторичных цеховых распределительных пунктов, как и на зажимах аппаратов, питаемых от первичных распределительных пунктов – 0,025 Ом;
4. Для аппаратуры, установленной непосредственно у электроприёмников, получающих питание от вторичных распределительных пунктов – 0,03 Ом.
Однако как показывают результаты расчётов для конкретных примеров, вышеприведенные значения переходных сопротивлений контактов являются завышенными, особенно для сетей, питающихся от трансформаторов мощностью выше 1000 кВА.
Значительное электрическое удаление систем электроснабжения от питающих центров позволяет считать, что при КЗ за понижающим трансформатором напряжение в точке сети, где он присоединён, практически остаётся неизменным и равным своему номинальному значению.
Сопротивления трансформаторов, кабелей, шинопроводов аппаратов берутся из справочников или по [17].
Имея величины сопротивлений всех элементов, входящих в схему замещения, определяют результирующие активные и индуктивные сопротивления короткозамкнутой цепи.
Активное сопротивление элементов аппаратуры и устройств, контактов, дуги в месте КЗ определяют в составе результирующего сопротивления:
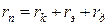 ,
,
здесь rk – преходное сопротивление контактного соединения токоведущих шин;
rэ – активное сопротивление элементов цепи КЗ;
rд – активное сопротивление дуги в месте КЗ.
Индуктивное сопротивление состоит из сопротивления внешней системы, понижающего трансформатора, шин, кабелей, катушек, автоматов и т. д.
Результирующие сопротивления rрез.б и хрез.б цепи КЗ находят путём преобразования схемы замещения с учётом активного переходного сопротивления. По найденным значениям активного и реактивного результирующих сопротивлений определяют (в килоамперах):
– начальное действующее значение периодической составляющей тока трёхфазного КЗ
 ; (13.22)
; (13.22)
– ударный ток трёхфазного КЗ:
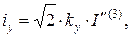 (13.23)
(13.23)
где 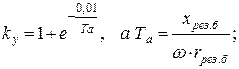
– действующее значение периодической составляющей тока однофазного КЗ, необходимое для выбора защиты от замыканий на землю:
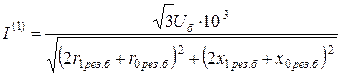 , (13.24)
, (13.24)
где 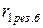 ,
, 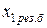 – результирующие активные и индуктивное сопротивления прямой последовательности, мОм;
– результирующие активные и индуктивное сопротивления прямой последовательности, мОм;
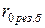 ,
, 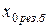 – результирующие активные и индуктивное сопротивления нулевой последовательности, мОм.
– результирующие активные и индуктивное сопротивления нулевой последовательности, мОм.
Пример 13.3. Рассчитать токи трёхфазного КЗ в точках К1 и К2 СЭС, схема которой изображена на рис. 13.5. Параметры элементов схемы указаны на рисунке. Электроустановки напряжением 0,4 кВ питаются через шинопровод типа ШМА-73.
Решение. Расчёт токов КЗ в точке К1. Сопротивления связи питающей подстанции с системой
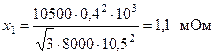 ;
; 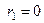 .
.
Сопротивления трансформатора:
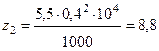 мОм;
мОм;
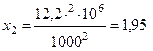 мОм;
мОм;
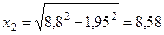 мОм.
мОм.
Сопротивления шины от выводов трансформатора сборных шин напряжением 0,4 кВ:
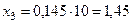 мОм;
мОм;
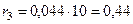 мОм.
мОм.
Индуктивное сопротивление токовой катушки расцепителя автомата QF1 на 1600 А, х4 = 0,06 мОм.
Сопротивления одновитковых первичных обмоток трансформатора тока ТА не учитываем. Результирующее переходное сопротивление при КЗ в точке К1 для трансформатора мощностью Sтр =1000 кВ·А, rн1 = 8,41 мОм.
|

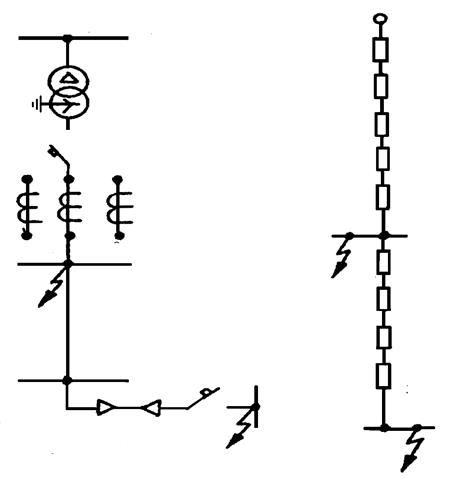
а б
Рис. 13.5. К примеру 13.3
Результирующие сопротивления короткозамкнутой цепи до точки К1:
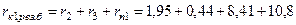 мОм;
мОм;
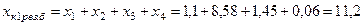 мОм.
мОм.
Полное сопротивление короткозамкнутой цепи
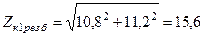 мОм.
мОм.
Начальное действующее значение периодической составляющей тока КЗ в точке К1
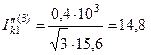 кА.
кА.
Ударный ток в точке К1:
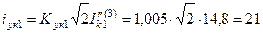 кА.
кА.
где 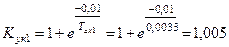 ;
;
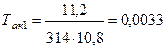 с.
с.
Расчёт токов КЗ в точке К2 . Сопротивление шинопровода ШМА-73:
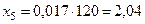 мОм;
мОм;
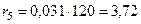 мОм.
мОм.
Сопротивления КЛ от шинопровода до выключателя QF2:
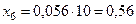 мОм;
мОм;
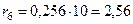 мОм.
мОм.
Индуктивное сопротивление токовой катушки расцепителя автомата QF2
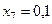 мОм.
мОм.
Результирующее переходное сопротивление в точке К2 с учётом коэффициента ступени КЗ принимаем 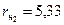 мОм.
мОм.
Результирующие сопротивления короткозамкнутой цепи К2:
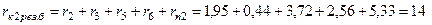 мОм;
мОм;
 мОм.
мОм.
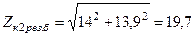 мОм.
мОм.
Начальное действующее значение периодической составляющей тока КЗ в точке К2
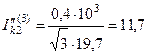 кА.
кА.
Ударный ток КЗ в точке К2
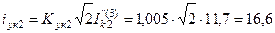 кА,
кА,
где 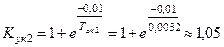 ,
,
причем 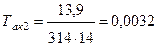 с.
с.
13.5. Активное сопротивление дуги в месте КЗ в установках
напряжением до 1000 В
При определении минимального значения тока КЗ в установках напряжением до 1000 В следует учитывать влияние на ток КЗ активного сопротивления электрической дуги в месте КЗ. Приближенные значения активного сопротивления дуги приведены в таблице 13.1.
Таблица 13.1
| Расчетные условия КЗ | Активное сопротивление дуги (мОм) при КЗ за трансформаторами мощностью, кВ.А | |||||||
| КЗ вблизи выводов низшего напряжения трансформатора | В разделке кабелей напряжением, кВ | 0,4 | ||||||
| 0,525 | 4,5 | 3,5 | 2,5 | |||||
| 0,69 | ||||||||
| В шинопроводе типа ШМА напряжением, кВ | 0,4 | – | – | – | ||||
| 0,525 | – | – | – | 3,5 | 2,5 | |||
| 0,69 | – | – | – | |||||
| КЗ в конце шинопровода типа ШМА длиной 100…150 м напряжением, кВ | 0,4 | – | – | – | 6-8 | 5-7 | 4-6 | |
| 0,525 | – | – | – | 5-7 | 4-6 | 3-5 | ||
| 0,69 | – | – | – | 4-6 | 3-5 | 2-4 |
При точных расчетах активное сопротивление дуги зависит от тока КЗ и длины дуги и рассчитывается по формуле
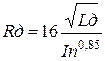 ,
,
где 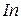 – начальное действующее значение периодической составляющей тока в месте КЗ, кА, опрделяемое с учетом сопротивления дуги;
– начальное действующее значение периодической составляющей тока в месте КЗ, кА, опрделяемое с учетом сопротивления дуги;
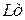 – длина дуги, см, которая принимается равной:
– длина дуги, см, которая принимается равной: 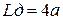 при
при 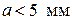 ;
; 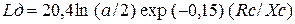 при
при 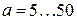 мм;
мм; 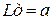
при  ; Rc, Xc – суммарные активное и индуктивное сопротивления цепи КЗ, мОм; а – расстояние между фазами проводников, мм.
; Rc, Xc – суммарные активное и индуктивное сопротивления цепи КЗ, мОм; а – расстояние между фазами проводников, мм.
Дата добавления: 2015-05-19; просмотров: 3346;
