Общий путь решения

Любая несимметрия характеризуется симметричными составляющими токов и напряжений в месте несимметрии. Следовательно, при двукратной несимметрии подлежат определению двенадцать неизвестных величин – по три симметричных составляющих токов и напряжений в каждой точке несимметрии. Для определения этих неизвестных нужно составить такое же число независимых уравнений.

В главах 7 и 8 и было установлено, что из граничных условий возникшей несимметрии непосредственно вытекают три соотношения для симметричных составляющих токов и напряжений в месте несимметрии. Таким образом, при двукратной несимметрии половина общего числа необходимых уравнений является следствием граничных условий. Остальные уравнения можно получить, рассматривая связи между токами и напряжениями одноименной последовательности. Так, при поперечных несимметриях одновременно в произвольных точках M и N заданной системы, схемы отдельных последовательностей которой после преобразований могут быть представлены в виде эквивалентных трехлучевых звезд
(рис. 12.1) для составляющих напряжений в точках M и N.

для прямой последовательности (рис. 12.1 а):

;

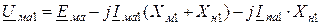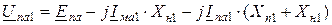. (12.1)

Для обратной последовательности (рис. 12.1 б):

;

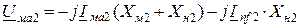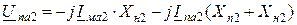. (12.2)

Для нулевой последовательности (рис. 12.1 в):

;

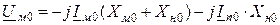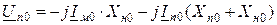. (12.3)

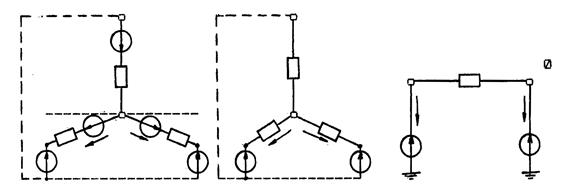
а б в

Рис. 12.1.Схемы прямой (а), обратной (б) и нулевой (в) последовательностей при несимметричных КЗ в двух точках М и N

Уравнения (12.1...12.3) и все соотношения, которые вытекают из граничных условий рассматриваемой двукратной несимметрии справедливы для любого момента времени переходного процесса.

При анализе сложных видов повреждений правило эквивалентности прямой последовательности при несимметрии в одной точке распространяется на двукратную несимметрию. Поэтому в таких случаях могут быть использованы все практические методы расчета, которые используются при однократной несимметрии.