Правило эквивалентности прямой последовательности. Из структуры выражений для тока прямой последовательности при рассмотренных видах однократной продольной несимметрии непосредственно следует

Из структуры выражений для тока прямой последовательности при рассмотренных видах однократной продольной несимметрии непосредственно следует, что этот ток можно определить как ток симметричного трехфазного режима в схеме, где несимметричный участок заменен симметричной цепью, величина сопротивления которой для каждого вида продольной несимметрии определяется сопротивлениями как самого несимметричного участка, так и схем обратной и нулевой последовательности относительно места несимметрии (рис. 11.13).

Таблица 11.1

Величина	Несимметрия одной фазы	Несимметрия двух фаз
Сопротивление в одной фазе	Разрыв одной фазы	Сопротивления в двух фазах	Разрыв двух фаз

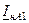
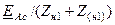
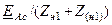
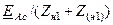
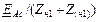
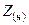
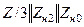
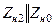
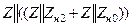
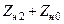
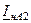
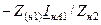
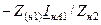
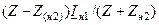
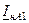
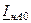
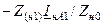
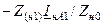
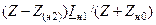
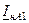
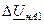
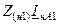
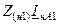
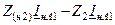
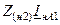
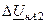
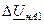
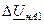
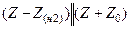
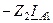
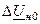
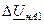
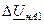
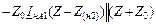
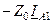
Изложенное положение представляет собой правило эквивалентности прямой последовательности применительно к условиям однократной продольной несимметрии. Оно аналогично этому правилу при однократной поперечной несимметрии и позволяет ток прямой последовательности в месте продольной несимметрии выразить в общем виде:

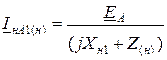, (11.25)

а падение напряжения прямой последовательности на несимметричном участке:

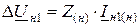(11.26)

где индекс (н) показывает вид продольной несимметрии, (н1) – при разрыве одной фазы, (н2) – при разрыве двух фаз.

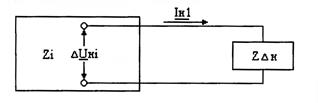
Рис. 11.13. К правилу эквивалентности прямой последовательности
при продольной несимметрии