Разрыв одной фазы
Основные уравнения падений напряжений в схемах каждой последовательности, составленные для симметричной части системы, при чисто индуктивной цепи можно представить в виде:
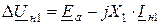 ;
;
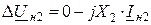 ; (11.2)
; (11.2)
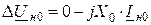 ,
,
где ΔUн1, ΔUн2, ΔUн0 – симметричные составляющие падения напряжения фазы А на несимметричном участке системы;
X1, X2, X0 – результирующие реактивности схем отдельных последовательностей относительно места продольной несимметрии.
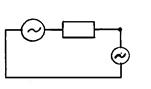
На рис. 11.4 изображен несимметричный участок системы, в которой возникла продольная несимметрия при разрыве фазы А.
Полагая, что разрыв фазы А происходит на малом отрезке, можно считать, что падения напряжений фаз В и С на длине этого участка равны нулю. В этом случае по месту несимметрии имеем следующие граничные условия, которые по структуре аналогичны граничным условиям двухфазного КЗ на землю.
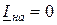 ,
, 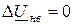 ,
, 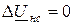 . (11.3)
. (11.3)
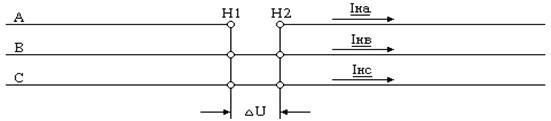
Рис. 11.4. Разрыв одной фазы
Следует отметить, что при разрыве фазы на протяженном участке или при отключении поврежденной фазы с обоих концов, граничные условия будут:
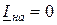 ;
;
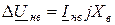 ; (11.4)
; (11.4)
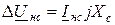 ,
,
где Iнв, Iнс – токи неповрежденных фаз;
Хв, Хс – реактивные сопротивления неповрежденных фаз по длине участка, на котором отключена поврежденная фаза А (т. е. сопротивления между точками Н1 и Н2).
В общем случае сопротивления 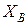 и
и 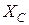 для токов различных последовательностей неодинаковы. Принципиальных трудностей при выводе расчетных выражений в этом случае не возникает, но математические выкладки получаются более громоздкими и в конечном итоге приводят к тем же выражениям, что и при использовании граничных условий в виде (11.3).
для токов различных последовательностей неодинаковы. Принципиальных трудностей при выводе расчетных выражений в этом случае не возникает, но математические выкладки получаются более громоздкими и в конечном итоге приводят к тем же выражениям, что и при использовании граничных условий в виде (11.3).
При разложении падений напряжений на симметричные составляющие с учетом граничных условий (11.3) получим:
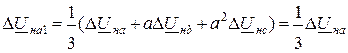 ;
;
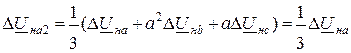 ; (11.5)
; (11.5)
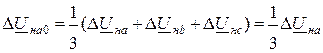 ,
,
т. е. 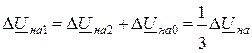 (11.6)
(11.6)
Напряжение между точками Н1 и Н2 поврежденной фазы А из (11.6) будет:
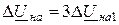 . (11.7)
. (11.7)
Из основных уравнений (11.1) с учетом (11.6) для симметричных составляющих Iна2 и Iно имеем:
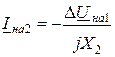 ;
; 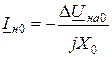 . (11.8)
. (11.8)
Расписав условие через симметричные составляющие тока и подставив вместо Iна2 и Iно их значения из (11.8), получим:
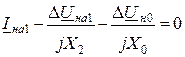 ,
,
откуда найдем 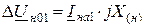 , (11.9)
, (11.9)
где 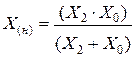 . (11.10)
. (11.10)
Теперь из (11.1) и (11.9) определим:
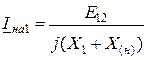 .
.
Из выражений (11.8) с учетом (11.10) для токов обратной и нулевой последовательностей имеем:
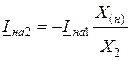 или
или 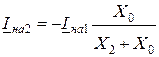 ; (11.11)
; (11.11)
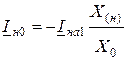 или
или 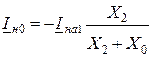 . (11.12)
. (11.12)
Для определения напряжений с одной из сторон продольной несимметрии следует предварительно найти по схемам отдельных последовательностей симметричной части сети соответствующие составляющие этих напряжений. Прибавив к последним соответствующие напряжения ∆U, находят симметричные составляющие напряжений с другой стороны продольной несимметрии.
Зная все симметричные составляющие токов и напряжений, можно определить фазные величины токов и напряжений. В частности, для определения фазных токов в месте разрыва одной фазы могут быть использованы выражения:
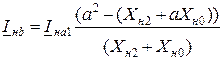 , (11.13)
, (11.13)
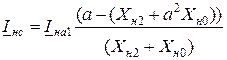 .
.
Для нахождения модуля фазных токов при разрыве одной фазы может быть использован коэффициент, определяемый по выражению:
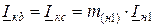 , (11.14)
, (11.14)
где 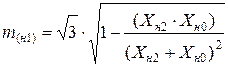 .
.
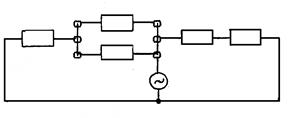
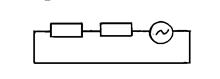
Соотношение (11.10) позволяет составить комплексную схему замещения (рис. 11.5) для случая разрыва одной из фаз.

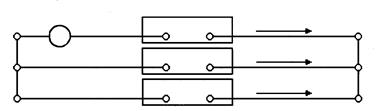
Рис. 11.5. Комплексная схема замещения при разрыве фазы
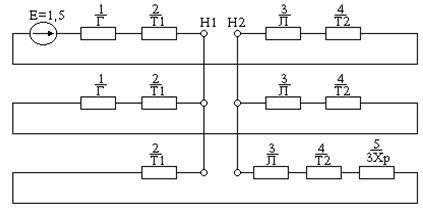
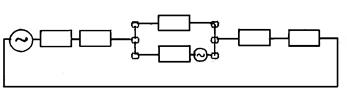
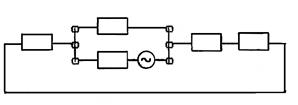
На рис. 11.6 а приведена схема, для которой составлена комплексная схема замещения (рис.11.6 б) при разрыве одной из фаз в начале линии. Складывая последовательно реактивности в схеме замещения обратной последовательности, получим:
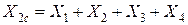 ,
,
и, соответственно, в схеме замещения нулевой последовательности:
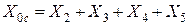 .
.
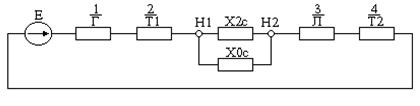
Комплексная схема замещения приводится к более простому виду (рис. 11.6 в). Результирующая ЭДС схемы прямой последовательности в данном случае численно равна Е1, а суммарное реактивное сопротивление
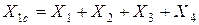 .
.
Суммарное сопротивление для определения токов прямой последовательности:
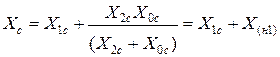 .
.

а
б
в
г
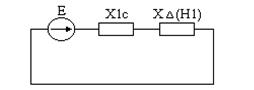
Рис. 11.6. а – расчётная схема, б – комплексная схема замещения
для случая разрыва одной фазы, в, г – преобразование схемы
Схема любой сложности при продольной несимметрии сводится к виду, изображенному на рис. 11.6 г. Следует всегда помнить, что в этой схеме результирующая ЭДС находится из схемы замещения только прямой последовательности относительно места несимметрии.
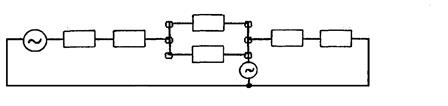
При решении задач необходимо иметь в виду принципиальное различие в преобразовании схем при продольной и поперечной несимметриях. В качестве примера на рис. 11.7 а показано, в чем состоит это различие. Все элементы исходной схемы пронумерованы и их номера сохранены для обозначения соответствующих элементов в схемах замещения отдельных последовательностей.


 а
а
б


в г


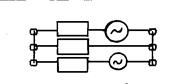
д е


ж з
Рис. 11.7. Пример составления схемы отдельных последовательностей
и определение результирующих ЭДС и сопротивлений для расчетной
схемы (а) при поперечной (б, в, г) и продольной (д, е, ж, з) несимметриях
При поперечной несимметрии в точке Н схема замещения прямой последовательности имеет вид, представленный на рис. 11.7 б. Проделаем следующее преобразование замещением элементов 1, 2, 3, 4 одним: Х11 =
= Х1 + Х2 + Х3║Х4 и элементов 5 и 6: Х9 = Х5 + Х6.
Для определения результирующей ЭДС и сопротивления относительно точки Н необходимо ветвь 9 с Е = 0 сложить параллельно с ветвью 11, имеющей ЭДС Е, т. е. Х1с = Х11║Х9.
В результате этих преобразований получим схему замещения прямой последовательности (рис. 11.7 в). Схема обратной последовательности и ее преобразования аналогичны, за исключением того, что в ней отсутствуют ЭДС источников. Схему нулевой последовательности (рис. 11.7 г) также можно преобразовать относительно точки Н: Х0с = (Х2 +
+ Х3║Х4)║(Х5 + 3Х7).
Предположим, что в точке Н возникла продольная несимметрия. В этом случае падение напряжения прямой последовательности в точке Н 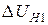 должно быть введено в рассечку цепи элемента 4 (рис. 11.7 д). Для определения результирующей ЭДС и сопротивления прямой последовательности относительно точки Н в данном случае необходимо вначале сложить последовательно элементы 11 и 9, т. е.
должно быть введено в рассечку цепи элемента 4 (рис. 11.7 д). Для определения результирующей ЭДС и сопротивления прямой последовательности относительно точки Н в данном случае необходимо вначале сложить последовательно элементы 11 и 9, т. е. 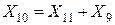 (рис. 11.7 е).
(рис. 11.7 е).
Затем образовавшуюся ветвь 10 с ЭДС Ен и ветвь 3 заменить эквивалентной: Х12=Х3║Х10, что дает искомую результирующую ЭДС относительно точки Н (рис. 11.7 г):
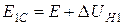 .
.
Результирующее сопротивление прямой последовательности:
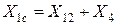 .
.
Схема обратной последовательности аналогична схеме рис. 11.7 д, но в ней отсутствуют ЭДС источника. Ее результирующее сопротивление определяется также, как и для схемы прямой последовательности.
Схема замещения нулевой последовательности приведена на
рис. 11.7 з. Для нахождения результирующего сопротивления схемы нужно сопротивление элемента 3 сложить параллельно с суммой сопротивлений элементов 2, 5, 3Х7 и затем прибавить сопротивление элемента 4.
Рассмотренный пример наглядно показывает разный подход к определению результирующих ЭДС и сопротивлений при поперечной и продольной несимметриях. Соотношение между величинами результирующих сопротивлений одноименной последовательности при этих несимметриях могут быть самыми различными в зависимости от характера схемы, места несимметрии, наличия обходных цепей.
Векторные диаграммы токов и напряжений. Для определения напряжения с одной из сторон продольной несимметрии (в данном случае разрыва одной фазы) следует предварительно найти по схемам отдельных последовательностей симметричной части цепи соответствующие составляющие этих напряжений. Прибавив к последним ΔUна1, ΔUна2, ΔUна0, находим симметричные напряжения с другой стороны продольной несимметрии.
Зная все симметричные составляющие токов и напряжений, определяют фазные величины токов и напряжений. В частности, для определения фазных токов в месте разрыва одной фазы могут быть использованы выражения (11.13), в которых ток Iка1 и реактивности X2 и X0 должны быть соответственно заменены током Ia1 и реактивностями X2 и X0. Аналогично для нахождения модуля фазных токов при разрыве одной фазы может быть использован коэффициент, определяемый по выражению (11.14). На рис. 11.8 приведены векторные диаграммы токов и напряжений в месте разрыва фазы А.

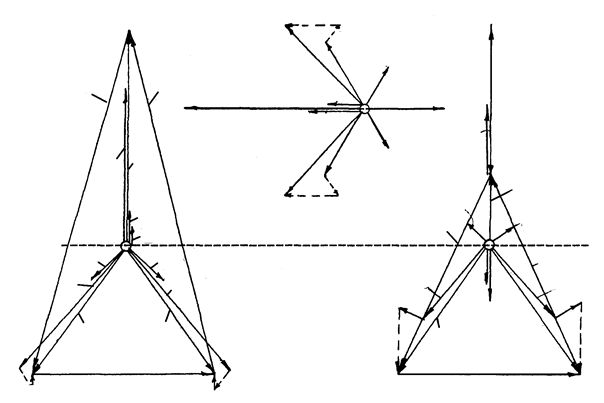
в г
Рис. 11.8. Векторные диаграммы токов и напряжений при разрыве
одной фазы трехфазной цепи (рис. 11.7): а – векторная диаграмма
токов в месте разрыва чисто индуктивной цепи; в и г – векторные
диаграммы напряжений поконцам разрыва (соответственно,
в точках Н1 и Н2)
Дата добавления: 2015-05-19; просмотров: 3199;
