Общие замечания

Продольную несимметрию в любой точке трехфазной системы можно представить включением в рассечку каждой фазы неодинаковых сопротивлений, которые могут быть связаны между собой взаимоиндукцией. Такой подход к решению задачи позволяет получить расчетные выражения в самом общем виде, но при этом необходимо проводить довольно сложные расчеты, а конечный результат представляется громоздкими выражениями. Поэтому значительно проще проводить решение для каждого вида продольной несимметрии, используя характеризующие его граничные условия.

Таким образом, продольная несимметрия может возникать вследствие неравенства фазных сопротивлений схемы или отдельных ее элементов при разрывах и отключениях одной или двух фаз трехфазной системы.

При возникновении в системе возмущающего воздействия в виде разрыва или несимметричного КЗ при наличии пофазного управления, релейная защита отключает поврежденную фазу (а при одновременном повреждении двух фаз – две фазы), оставляя в работе неповрежденные фазы. При одноцепных ЛЭП таким отключением исключается потеря связи между отдельными станциями или генераторами и приемниками. При эксплуатации пофазное отключение производится не только в аварийных условиях, но и при проведении ремонтных, профилактических и испытательных работ.

Режим работы системы с одной или двумя отключенными фазами является несимметричным и связан с дополнительными потерями мощности, опасным перегревом двигателей и генераторов при длительной их работе в неполнофазном режиме. Линии электропередачи при неполнофазном режиме оказывают значительное мешающее и опасное электромагнитное влияние на коммуникации при сближении их с ЛЭП. Вследствие этого возникает необходимость в количественной оценке фазных токов и напряжений при всех возможных видах продольной несимметрии (разрывах или отключении одной или двух фаз).

Расчет переходных процессов при продольной несимметрии удобно производить с помощью метода симметричных составляющих, предполагая, что несимметрия имеет местный характер, а внешняя система продолжает оставаться конструктивно симметричной (рис. 11.1). Тогда для симметричной части схемы, составленной по параметрам трех последовательностей, могут быть записаны уравнения:

,

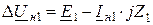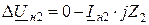, (11.1)

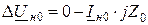
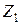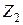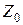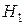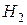где , , – полные результирующие сопротивления соответствующих последовательностей относительно места продольной несимметрии, т. е. относительно точек и (рис. 11.1);

ΔU_н1, ΔU_н2, ΔU_н0 – симметричные составляющие падений напряжений по месту несимметрии (т. е. напряжения между точкам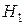и и 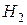). Индекс Н является признаком продольной несимметрии.

Уравнения (11.1) содержат неизвестные величины: ΔU_н1, ΔU_н2, ΔU_н0, I_н1, I_н2, I_н0, для определения которых следует иметь еще три уравнения, которые можно получить из граничных условий по месту несимметрии для заданного вида продольной несимметрии.

а

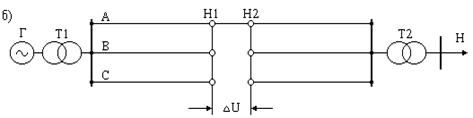
б

Рис. 11.1. Продольная несимметрия в трехфазной системе:
а – при разрыве фазы А; б – при разрыве фаз В и C

11.2. Схемы замещения прямой, обратной и нулевой
последовательностей при продольной несимметрии

Схема замещения прямой последовательности является такой же схемой, которую составляют для любого симметричного трехфазного режима. В зависимости от применяемого метода расчета и момента времени в нее вводят генераторы и нагрузки соответствующими сопротивлениями и ЭДС, а все остальные элементы вводят в схему замещения неизменными сопротивлениями.

Схема замещения обратной последовательности по структуре аналогична схеме прямой последовательности. Различие между ними состоит в том, что в схеме обратной последовательности ЭДС всех генерирующих ветвей условно принимают равными нулю, а реактивные сопротивления обратной последовательности синхронных машин и нагрузок считают практически постоянными и не зависящими от вида возникшей несимметрии.

Началом схем прямой и обратной последовательностей (точка нулевого потенциала схемы) считают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей.

При продольной несимметрии схемы прямой и обратной последовательностей имеют два конца – ими являются две точки, между которыми расположена продольная несимметрия. Между концами схем отдельных последовательностей приложены напряжения соответствующих последовательностей, возникшие в месте несимметрии (рис. 11.2 а, б).

Составление схемы нулевой последовательности начинают от точки, где возникла несимметрия, считая, что в этой точке все фазы замкнуты между собой накоротко (рис. 11.2 в) и напряжение нулевой последовательности ΔU_о приложено в рассечку фазных проводов.

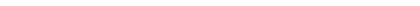
а б в

Рис. 11.2. Включение источника при продольной несимметрии:
а – прямой последовательности; б – обратной последовательности;
в – нулевой последовательности

Далее выявляются в пределах каждой электрически связанной цепи возможные пути протекания токов нулевой последовательности. При продольной несимметрии циркуляция токов нулевой последовательности возможна даже при отсутствии заземленных нейтралей.

Сопротивление, через которое заземлены нейтрали трансформатора, генератора и т. д., должно быть введено в схему нулевой последовательности утроенной величиной. Это обусловлено тем, что схему нулевой последовательности составляют для одной фазы, а через указанное сопротивление протекает сумма токов нулевой последовательности трех фаз.

а

б

в

г

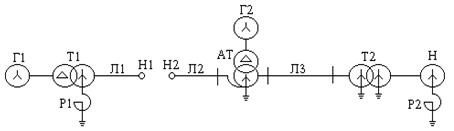
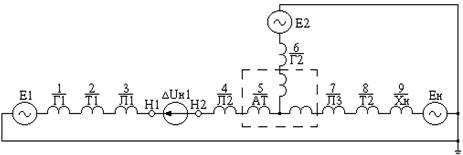
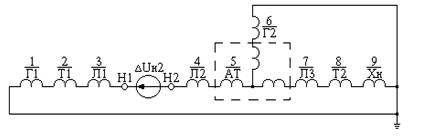
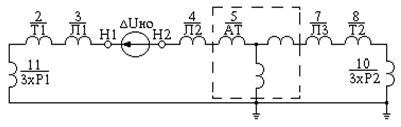
Рис. 11.3. Пример составления схем отдельных
последовательностей при продольной несимметрии:
а – расчётная схема; б, в, г – схемы замещения прямой,
обратной и нулевой последовательностей

Началом схемы нулевой последовательности считают точку, в которой объединены ветви с нулевым потенциалом. При продольной несимметрии схема нулевой последовательности имеет два конца – границы места несимметрии, т. е. точки, где возникла несимметрия (точки Н₁ и Н₂ на рис. 11.2).

Сопротивления прямой, обратной и нулевой последовательностей элементов систем электроснабжения рассчитываются также, как и при поперечной несимметрии.

Исходная схема и пример составления схем отдельных последовательностей показан на рис. 11.3.