Разрыв двух фаз

В случае разрыва фаз В и С в месте несимметрии (рис. 11.9) имеем следующие граничные условия:

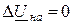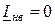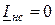, , , (11.15)

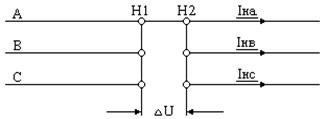
Рис. 11.9. Разрыв двух фаз

Симметричные составляющие токов с учетом (11.15) будут:

;

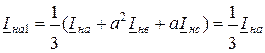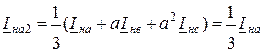; (11.16)

,

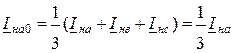т. е. 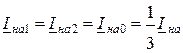(11.17)

Учитывая (11.15), ΔU_на = ΔU_на1 + ΔU_на2 + ΔU_на0 = 0, и, подставляя в это уравнение вместо симметричных составляющих напряжений и их значений из (11.2) с учетом соотношений (11.17), получим:

,

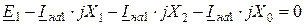откуда

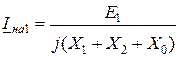(11.18)

или

,

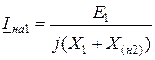где Х_(н2)= Х₂ + Х₀.

Ток в поврежденной фазе А из (11.17):

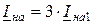(11.19)

Симметричные составляющие падения напряжения в месте несимметрии:

;

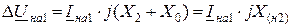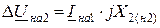; (11.20)

.

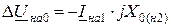Для определения фазных величин достаточно произвести суммирование соответствующих симметричных составляющих.

Рис. 11.10. Комплексная схема замещения при разрыве двух фаз

Согласно выражению (11.18) комплексная схема замещения имеет вид, приведенный на рис. 11.10, а на рис. 11.11 приведены векторные диаграммы токов и напряжений в месте разрыва фаз В и С

а б

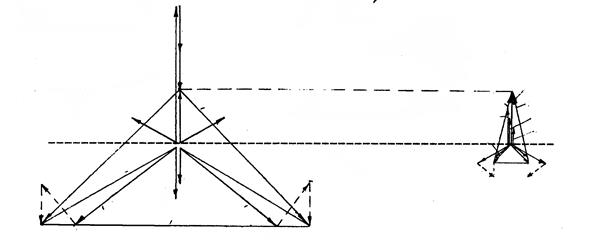
в г

Рис. 11.11. Разрыв двух фаз В и С трехфазной цепи: а – исходная схема;
б – векторная диаграмма токов в месте разрыва; в и г – векторные
диаграммы напряжений по концам разрыва (соответственно, в точках Н1 и Н2)