РАДИОТЕХНИЧЕСКИХ СИСТЕМ

ИНФОРМАЦИОННАЯ ТЕОРИЯ

В настоящем междисциплинарном учебном пособии рассматриваются основные теоретические вопросы, связанные с процессами формирования, преобразования, хранения и передачи информации в системах электросвязи вообще и в радиотехнических системах в частности – прикладная теория информации, или информационная теория радиотехнических систем.

Проблемы прикладной теории информации (ПТИ) излагаются на базе обычной математической подготовки студентов инженерных специальностей, в основном применительно к системотехническому проектированию оптимальных радиоэлектронных систем передачи информации по критериям эффективности использования каналов радио- и электросвязи, а также их информационной надёжности.

Усвоение студентами материалов пособия даст им математическую основу для углублённого изучения таких общепрофессиональных и специальных дисциплин, а также дисциплин специализации, как «Радиотехнические системы», «Статистическая теория радиотехнических систем», «Радиотехнические системы передачи информации», «Устройства приёма и обработки сигналов», «Системы и сети подвижной радиосвязи», «Дискретная и цифровая обработка сигналов в РТС» и т. п. Желающие более подробно изучить математические основы теории информации, например с целью получения магистерской степени в области информационных систем, могут затем перейти к «чисто математической» литературе.

Пособие может использоваться при подготовке магистров техники и технологии, а также специалистов и аспирантов по специальностям, связанным с проектированием, разработкой и эксплуатацией различных систем электросвязи.

Пособие может быть полезно студентам, обучающимся по специальностям, которые связаны с различными видами информации и её количественными свойствами.

В В Е Д Е Н И Е

Понятие «информация» является весьма широким общенаучным гуманитарно-философским понятием. Впервые в прикладные разделы математики понятие информации было введено, по-видимому, в 1921 г. английским математиком Рональдом Фишером (1890-1968): при разработке метода максимального правдоподобия он назвал величину, обратную дисперсии «наилучшей оценки» параметра распределения вероятностей некоторойнепрерывной скалярной случайной величины, количеством информации, содержащейся в статистической выборке относительно неизвестного параметра распределения.

В 1924 г. американский физик и инженер шведского происхождения Гарри Найквист (1889-1976) ввёл логарифмическую меру количества информации, которое содержится в сообщении, передаваемом с помощью «многоуровневого телеграфа»: 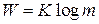, где W – скорость передачи информации, m – количество используемых в телеграфе уровней тока, K – некоторая константа.

В 1928 г. американский инженер Ральф Хартли (1888-1970) ввёл количественную меру для знаковой (семиотической) информации: если по каналу связи передаётся один из независимых равновероятных знаков u_j алфавита {u_j; j = = 1, 2, …, N }, то количество передаваемой по каналу информации I₀, приходящееся на один знак, равно I₀ = log _a N. Количество информации I_n, содержащейся в i-й последовательности S_i⁽ⁿ⁾ из n независимых равновероятных знаков S_i⁽ⁿ⁾ = = (u_i1, u_i2, …, u_in), равно сумме соответствующих элементарных количеств информации: I_n = n I₀ = n log _a N.

В 1948 г. появилась фундаментальная работа американского инженера и математика Клода Шеннона (1916-2001: [46], с. 243-332), в которой он обобщил информационный подход Найквиста и Хартли на произвольные знаковые системы и получил ряд основополагающих результатов математической теории систем связи, позволяющих количественно охарактеризовать качество функционирования различных каналов связи при отсутствии и при наличии в канале связи всевозможных естественных, промышленных и преднамеренных помех.

Идеи К. Шеннона оказались настолько глубокими и убедительными, что информационный подход стал формально применяться ко всевозможным техническим и не-техническим системам. Многозначность термина «информация» привела к большой путанице и всевозможным неоправданным обобщениям. Поэтому уже в 1956 г. основоположник математической теории информации выступил с краткой заметкой «Бандвагон», в которой предупреждал об опасности безоглядного применения его теории во всевозможных областях человеческого знания. В частности, о самой теории информации К. Шеннон написал следующее ([46], с.667-668):

«Появившись на свет в качестве специального метода в теории связи, она заняла выдающееся место, как в популярной, так и научной литературе.»

«… глубокое понимание математической стороны теории информации и её практических приложений к вопросам общей теории связи является обязательным условием использования теории информации в других областях науки.»

«… поиск путей применения теории информации в других областях … осуществляется в длительном процессе выдвижения новых гипотез и их экспериментальной проверки».

Наиболее плодотворное развитие и использование методология К. Шеннона получила в следующих областях знаний.

Математическая («чистая», абстрактная) теория информации, в которой исследуются различные формализованные информационные меры (статистическая, вероятностная, топологическая, алгоритмическая, семантическая, прагматическая и т. п.) и их математические свойства.

Физическая теория информации, в которой выясняются вопросы, связанные с количеством энергии, затрачиваемой на выработку данного количества измерительной (метрологической) информации («демон Максвелла» и т. п.).

В экспериментальной биологии и инженерной психологии применение теории информации даёт возможность проводить оптимальное планирование экспериментов, количественный анализ их результатов, а также выявлять общие закономерности переработки информации у животных и у человека.

Достаточно успешное применение теория информации находит в теоретической лингвистике.

Мы будем рассматривать применение теоретико-информационного подхода к проектированию эрготехнических («человеко-машинных») информационных систем (ЭТИС) и в особенности – к оптимизации радиотехнических подсистем электросвязи таких систем.

Применительно к радиотехническим и телекоммуникационным системам, развитие которых, собственно, и привело к возникновению теории информации, основными системотехническими проблемами являются эффективность использования различных каналов связи и их информационная надёжность (помехоустойчивость) в условиях воздействия на аппаратуру канала передачи и приёма сообщений естественных, искусственных (промышленных) и организованных (преднамеренных) помех. Эти проблемы на системотехническом уровне решаются в рамках статистической теории радиотехнических систем и статистической теории систем электросвязи. Теория информации является математической основой для решения статистических задач оптимизации такого рода систем.

Однако непосредственное использование результатов (теорем) математической теории информации, как и вообще современной («чистой») математики, для технических приложений вызывает большие психологические трудности, поскольку стиль мышления и математическая подготовка математиков и инженеров принципиально различны. Как пишет Р. Фишер в своей прикладной монографии «Статистические методы для исследователей» ([36], с. 7-8):

«... практическое применение общих теорем – это совсем иное дело, чем их установление при помощи математических доказательств. Всё, что требуется

для практического применения, – это достаточно глубокое понимание самого смысла этих теорем, что вполне доступно и без знакомства с доказательствами».

В настоящем учебном пособии автор попытался изложить основные практические результаты теории информации, которая основана на статистической информационной мере Шеннона, на базе обычной математической подготовки студентов технических специальностей, которую они получают на первых курсах обучения.

Вначале проанализированы исторические и технические предпосылки появления прикладной теории информации (ПТИ), что позволяет проследить историческую логику развития теории и причину широкого общенаучного резонанса, вызванного появлением этой теории. Такой анализ позволяет чётко определить основную проблематику теории ПТИ, логику её построения и «не заблудиться» в многочисленных её обобщениях и ответвлениях. Об этой опасности «заблудиться» предупреждал К. Шеннон более полувека назад.

Далее определяется общая структура информационной эрготехнической системы, описывается её функционирование, роль основных компонентов системы ЭТИС и основные задачи системотехнического проектирования оптимальных подсистем передачи и приёма сообщений различных систем ЭТИС – и вводится статистическая мера количества информации К. Шеннона для знаковых (семиотических) систем.

В разделе «Информационная статика» анализируются основные характеристики источников знаковых («дискретных») сообщений (ДИС), даётся понятие об оптимальном кодировании сообщений, выдаваемых источником ДИС. Рассматриваются потери информации в статических системах передачи знаковой (семиотической, «дискретной») информации, вводится удельная информационная ёмкость (энтропия) и информационная надёжность статического канала передачи сообщений, даётся понятие о помехоустойчивом канальном кодировании сообщений источника ДИС.

Рассматриваются различные количественные меры измерительной (метрологической) информации, анализируется информационная мера Р. Фишера и решается проблема округления результатов измерений в метрологии.

Наконец рассматривается передача знаковой (семиотической) информации с помощью аналоговых систем передачи, содержащих на своём входе цифро-аналоговые преобразователи, роль дифференциальной энтропии Шеннона и проблема квантования в статических каналах передачи знаковых (дискретных) сообщений. Анализируются различные статические многоуровневые каналы передачи сообщений, в том числе использующие аналого-цифровые и цифро-аналоговые преобразователи сигналов.

В разделе «Информационная динамика» рассматриваются ответы на вопрос, каким образом фактор времени влияет на функционирование систем ЭТИС и каковы основные статистические характеристики динамических систем передачи семиотической (дискретной) и метрологической (аналоговой) информации. В том числе решается проблема дискретизации (теорема Котельникова-Шеннона) и проблема максимальной скорости телеграфирования (интервал Найквиста). Рассматриваются также численные методы расчёта пропускной способности современных цифровых каналов радиосвязи третьего и четвёртого поколений.

Завершает учебное пособие итоговое заключение, библиографический список, предметный и именной указатели, список основных сокращений и условных обозначений.

В качестве приложений даются основные понятия общей теории информации, сведения об основных достижениях специалистов Белловских телефонных лабораторий (в которых сформировалась математическая теория электросвязи) в области ПТИ, об основных этапах развития теории кодирования, о различных подходах к выводу так называемой формулы Шеннона, а также даются краткие биографии основных создателей теории ПТИ.

Вопросы для самопроверки

1. Кто и когда ввёл в теорию электросвязи логарифмическую меру количества информации?

2. Кто и когда заложил математические основы прикладной теории информации?

3. Какие ветви общей теории информации получили наибольшее развитие?

4. Какие основные проблемы систем радио- и электросвязи должна помогать решать прикладная теория информации?

5. Каково общее содержание информационной статики и информационной динамики?