Исторические и технические предпосылки ПТИ

Проблематика и основные задачи прикладной теории информации (ПТИ) формировались и эмпирически решались в процессе развития технических средств передачи информации [4, 5, 27, 48, 60]. В Прил. 5 даны краткие биографии инженеров и учёных, фамилии которых выделены полужирным курсивом.

Первым телекоммуникационным средством передачи информации нового времени следует считать семафорный («оптический») телеграф – систему визуальной передачи сообщений посредством семафорной азбуки. Телеграф был изобретён в 1792 г. французским монахом Клодом Шаппом (1763-1805), который вместе со своими братьями построил и ввёл в эксплуатацию телеграфную линию Париж–Лилль (1794 г., длина линии 225 км). Здесь выявилась Пробле-ма №1 ПТИ: способы кодирования знаковых (цифро-буквенных) сообщений (проблема кодирования сообщений).

Самая длинная в мире линия семафорного телеграфа действовала в 1839-1854 гг. и связывала между собой С.-Петербург и Варшаву (1200 км). Сигнал по этой линии проходил за 15 мин (эквивалентная скорость распространения сигналов приблизительно 4 Маха).

Предпринимаемые учёными Европы многочисленные попытки создания телеграфных линий на основе электростатических и электролитических явлений не приводили к заметным успехам.

В 1820 г. датский физик Ханс Эрстед (1777-1851) открыл действие электрического тока на магнитную стрелку, а французский физик Андре Ампер (1775-1836) 2 октября 1820 г. предложил использовать это явление в телеграфии. В том же 1820 г. австрийский физик Иоганн Швейггер (1779-1857) изобрёл так называемый «мультипликатор»: электромагнитный прибор, в котором при подаче тока той или иной полярности с помощью соленоида отклонялась горизонтально расположенная магнитная стрелка вправо или влево от равновесного состояния, определяемого геомагнитным полем.

Синтез идей предшественников удачно реализовал русский электротехник и востоковед Павел Львович Шиллинг (1786-1837). В 1832 г. он продемонстрировал работу электромагнитного телеграфа на основе однопроводной электрической линии и одного мультипликатора на приёмной стороне линии. Для ручного кодирования сообщений на передающей стороне линии применялся специальный ключ, а для визуального декодирования – специально обученный телеграфист должен был пользоваться бинарным последовательным неравномерным кодом. В этом коде П. Л. Шиллинг учёл частотности букв русского и английского языков (частотность появления букв в длинных текстовых сообщениях). Так, английской букве “e” соответствовало одно отклонение стрелки «вправо», букве “i ” – два последовательных отклонения «вправо» и т. д.

При подготовке к Боннскому съезду немецких естествоиспытателей и врачей, на который прибыли естествоиспытатели и врачи ведущих промышленных стран мира, Шиллинг изготовил пятиканальный телеграфный аппарат, в котором можно было, для наглядности демонстрации, фиксировать пять клавишей на передающей стороне телеграфа и видеть положение пяти магнитных стрелок на приёмной стороне. Для этого аппарата Шиллинг разработал бинарный параллельный равномерный пятипозиционный код (прообраз кода Бодо). Здесь выявилась Проблема №2 ПТИ: критерии сравнения различных способов кодирования знаковых сообщений и выбор наилучшего (оптимального) способа кодирования (проблема кодирования источника дискретных сообщений).

До сих пор коды Шиллинга считаются достаточно совершенными [48].

Достижения П. Л. Шиллинга, продемонстрированные в Бонне в 1835 г., были высоко оценены мировой научной общественностью. Известный русский математик В. Я. Буняковский (1804-1889) решил заняться математическими исследованиями по теории кодирования. Великий Карл Гаусс начал переписку с Шиллингом и побудил своего ученика Карла Штейнгейля (1801-1870) заняться разработкой на основе аппарата Шиллинга пишущего мультипликаторного те-

леграфа, который Штейнгейль и продемонстрировал 27 января 1838 г.

К тому времени П. Л. Шиллинг скончался, а его дело продолжил, специально переехавший для этого из Германии в Россию в 1835 г., Борис Семёнович (Мориц Герман) Якоби (1801-1874). В 1839 г. Якоби, при содействии российского физика Эмилия Христиановича Ленца (1804-1865), построил пишущий телеграф с электромагнитом и якорем на приёмной стороне. В 1841 г. телеграф Якоби был введён в эксплуатацию между Зимним дворцом и Главным штабом, а в 1843 г. – между Петербургом и Царским Селом (25 км, с подземным кабелем). Американский изобретатель С. Морзе получил патент на свой электромагнитный телеграф только в 1847 г.

Николай I «высоко оценил» работы Б. С. Якоби: 18 апреля 1844 г. он запретил публикацию трудов по телеграфии из «секретных государственных соображений». И даже речь Якоби «Об электротелеграфии», опубликованная в бюллетене Петербургской Академии наук “Recueil de actes”, была изъята из всех уже отпечатанных экземпляров. А в 1850 г. царское правительство подписало контракт с немецкой фирмой «Сименс и Гальске» на «телеграфизацию всей России». Б. С. Якоби оказался отстранённым от телеграфного дела.

В Сев. Америке в эти времена не было даже семафорной телеграфии, и Конгресс США в 1837 г. объявил конкурс на лучший проект семафорного телеграфа. Вместо семафорного телеграфа профессор живописи Сэмюэль Морзе (1791-1872) представил проект пишущего электромагнитного телеграфа. Демонстрация модели аппарата С. Морзе в Нью-Йоркском университете 4 сентяб-

ря 1837 г. прошла неудачно; добиться реальных результатов Морзе смог только в 1844 г. – на основе разработанного в 1838 г., совместно с А. Вайлом, последовательного неравномерного кода, в котором использовалось три символа: «точка», «тире» и «пауза». В коде Морзе, так же, как и в коде Шиллинга, была учтена эмпирическая частотность знаков английского языка.

Дальнейшее развитие мировой телеграфии развивалось в направлении автоматизации процессов кодирования и декодирования, удлинения линий теле-

графной связи, уплотнения каналов и увеличения надёжности телеграфии.

При создании в 1840-х годах телеграфной линии Вашингтон–Балтимор Морзе столкнулся с явлением «расплывания точки» на приёмном аппарате, которое ограничивало скорость телеграфии. Для повышения этой скорости изобрели двухполюсный телеграф, в котором «точка» передаётся положительным импульсом, а «тире» – отрицательным той же длительности. Возникла Проблема №3 ПТИ: предельно достижимая скорость передачи «дискретной» информации при ограниченной полосе пропускания канала связи.

В 1855 г. американский физик Дэвид Юз (1831-1900) разработал буквопечатающий телеграфный аппарат с непрерывно вращающимся на приёмной стороне тúповым (то есть имеющим печатные литеры) колесом, которое работало по импульсно-селекционному коду. Через некоторое время Д. Юз переехал в Европу и там широко внедрял свои аппараты. В 1865 г. он был приглашён в Россию. Аппарат Юза имел скорость телеграфирования до 200 знаков в минуту.

В 1874 г. американский инженер-изобретатель Томас Эдисон (1847-1931) – дальний родственник К. Шеннона – изобрёл, совместно с инженером Дж. Прескоттом, квадруплексный (учетверённый) телеграф, в котором использовался не только признак полярности токовых посылок, но и их относительных амплитуд. Получилось два телеграфных канала в одной линии связи с кодовым разделением каналов. Дальнейшее увеличение количества используемых для кодирования уровней амплитуд посылок наталкивалось на трудности их различения – из-за воздействия на сигналы в телеграфных линиях различных элек-трических помех. Возникла Проблема №4 ПТИ: теоретическая оценка оптимального количества уровней при передаче знаковой информации по аналоговым каналам связи с помехами (проблема квантования). Проблема № 4 решена практически лишь в наше время – в системах подвижной радиосвязи с многопозиционной фазовой или амплитудной манипуляцией, а также с квадратурной амплитудной модуляцией.

Нерешённой в середине XIX оставалась также задача «исключения человеческого фактора» из процесса передачи телеграмм: опытный телеграфист мог передавать 250-300 знаков в минуту. Поэтому необходимо было отделить этап сравнительно медленного ручного набора телеграмм многими телеграфистами, с их индивидуальными скоростями, от этапа автоматической передачи телеграмм с предельной скоростью телеграфной линии связи.

В 1867 г. английский электромеханик Чарльз Уитстон (1802-1875) разработал передающий телеграфный аппарат, работающий от перфоленты с обычным кодом Морзе.

В 1874 г. французский механик Жан Морис Эмиль Бодо (1845-1903) запатентовал двукратный последовательный телеграфный аппарат на основе пятиразрядного равномерного кода. В коде Бодо каждый знак представляется пятипозиционными посылками тока одинаковой длительности. Телеграмма предварительно набирается на перфоленте, на которой также имеется равномерная дорожка с более мелкими отверстиями – для синхронизации приёмного телеграфного аппарата. В 1877 г. заработала телеграфная линия Париж–Бордо длиной в 500 км с автоматическими телеграфными аппаратами Ж. Бодо.

В 1894 г. Бодо изобрёл также систему распределения для одновременной (мультиплексной) передачи нескольких телеграмм по одной и той же телеграфной линии (временнóе разделение каналов). Скорость передачи телеграфных сообщений Бодо довёл до 1000 знаков в минуту.

В телеграфе Бодо можно также повторять переданные телеграфные знаки дважды или четырежды (в зависимости от «важности» телеграфного сообще-

ния). Выявилась Проблема №5 ПТИ: оценивание информационной надёжности различных систем передачи знаковых сообщений (проблема расчёта пропускной способности каналов электросвязи).

Многочисленные (начиная с 1858 г.) попытки проложить трансатлантический телеграфный кабель увенчались успехом лишь в 1866 г. Однако обнаружилось, что передавать телеграммы по такому длинному кабелю с помощью

существовавшей на тот момент аппаратуры невозможно по двум причинам: сильное затухание на линии – из-за омических потерь в кабеле и очень малая скорость телеграфирования – вследствие огромной ёмкости кабеля и соответствующего «затягивания» телеграфных посылок.

Снова встал теоретический вопрос о предельно достижимой скорости передачи знаковых сообщений.

Кроме того, пришлось существенно увеличить чувствительность приёмного телеграфного аппарата, которую в 1866 г. английский физик и математик Уильям Томсон (лорд Кельвин: 1824-1907) повысил с 10 мА до 0,02 мА! А это обострило Проблему № 4: влияние электрических помех на надёжность передачи сообщений.

Для повышения пропускной способности телеграфных линий связи предпринимались попытки использовать резонансные явления для частотного разделения каналов связи. Одному из первых это удалось сделать французскому учителю физики А. Лаборду в 1860 г. – за счёт прерываний тока с различными частотами. Ещё в 1854 г. французский механик Ш. Бурсель предложил использовать зависимость частоты прерываний тока в обмотке электромагнита с мембраной для передачи человеческой речи по электрическому проводу. В 1860 г. Ф. Рейс придумал, как реализовать эту идею Бурселя, и изготовил модель телефона. На этой же основе А. Лаборд сделал макет «гармонического телеграфа». Более совершенную модель такого телеграфа разработал в 1869 г. профессор Харьковского университета Ю. И. Морозов. Он использовал на передающем аппарате модуляцию тока в проводящей жидкости гармоническим сигналом.

Для этого в передающем аппарате в солёную воду помещалось два электрода, включённых последовательно с батареей телеграфной линии. Второй электрод («язычок») был выполнен в виде лёгкой пружинки и мог колебаться с соответствующей резонансной частотой. При этом расстояние между электродами изменялось со звуковой частотой – в телеграфную линию подавались почти синусоидальные колебания тока. На приёмном аппарате соответствующий пружинный электрод приходил в резонансное колебание.

Впоследствии «гармонический телеграф» реализовался в современном тональном (300-3400 Гц) и надтональном (3-10 кГц) способах телеграфирования. Синтез всего лучшего из достижений, накопленных в телеграфии в XIX в., привёл к созданию старт-стопного буквопечатающего телеграфного аппарата с равномерным кодом – телетайпа (1914-1918 гг., США).

В 1874 г. Президент американской телеграфной компании Western Union Вильям Ортон заказал изобретателям Т. Эдисону и Э. Грею найти способ передачи по одной телеграфной линии одновременно нескольких сообщений. В это же время шотландский профессор физиологии из Бостонского университета (США) Александр Белл (1847-1922), который занимался обучением глухих детей и много лет работал над проблемой передачи звука с помощью электропроводов, также решил заняться «гармоническим телеграфом». 2 июня 1875 г. его помощник Т. Уотсон «случайно» выдернул один из язычков резонатора в передающем аппарате «гармонического телеграфа», а Белл на приёмном аппарате уловил ворчание Уотсона и понял, что его многолетняя мечта о передаче звука по электропроводам близка к осуществлению.

Через восемь месяцев Белл добился полного успеха, и 14 февраля 1876 г. тесть Белла подал от его имени в Вашингтонское бюро патентов заявку на «Телеграфное устройство, при помощи которого можно передавать человеческую речь». В тот же день в бюро явился Э. Грей с предварительной заявкой на «Устройство для передачи и приёма вокальных звуков телеграфным способом». Но Грей опоздал на несколько часов: заявка Белла уже была зарегистрирована, а 7 марта 1876 г. А. Белл получил Патент США №174 465 на систему телефонной связи. Белл, кроме прочих достоинств, обладал исключительными организаторскими способностями. В 1877 г. он создал фирму Bell Telephone C ^о. В 1879 г. он приобрёл у компании Western Union права на патент угольного микрофона Эдисона, что сделало телефон Белла очень практичным. Уже к 1886 г. фирма Белла имела абонентскую сеть в 150 тыс. частных телефонов, а фирма Western Union до наших дней занимается международными денежными телеграфными переводами.

Заслуги А. Белла заключаются не только в изобретении практичного телефона, но и в успешном развитии телефонии на строго научной основе. В 1881 г. он приобрёл фирму Е. Бартона и Э. Грея Western Electric и выделил из неё кадры для вновь созданной компании Western Electric Research Laborato-ries, а в 1922 г. организовал выпуск ныне всемирно известного научно-тех-нического журнала “Bell Technical System Journal”. С 1897 г. Белл регулярно привлекал к предоставлению консультаций для своих инженеров американского математика Георга Кэмпбелла (1870-1954), принятого на работу в фирму Белла American Telephone and Telegraph (AT&T ).

Уже после смерти А. Белла (1922 г.) его последователи из созданной Беллом в 1885 г. дочерней фирмы AT&T и купленной Беллом у фирмы Western Union компании Western Electric организовали общую дочернюю компанию Bell Telephone Laboratories (Bell Labs), направив её деятельность на разработку и авторское сопровождение выпускаемого фирмой Western Electric телефонного оборудования, а также на фундаментальные и прикладные научные исследования в области радиоэлектроники. В компанию Bell Labs влилась компания Western Electric Research Laboratories и вошла часть конструкторского отдела фирмы AT&T.

В 1925 г. в составе компании Bell Labs была организована Математическая лаборатория, начальником которой стал Т. Фрай – руководитель группы математиков компании Western Electric [52]. Это позволило сконцентрировать

по существу в одном из первых промышленных Научно-исследовательских институтов лучшие научные кадры, исследовательские и конструкторские работы которых финансировались родительскими фирмами Western Electric и AT&T.

В компании Bell Labs работали такие всемирно известные учёные, как радиофизики Дж. Карсон, Р. Хартли, Г. Найквист и С. Райс, математики Г. Кэмпбелл, Р. Хэмминг, Л. Макколл и К. Шеннон (все из Математической лаборатории БТЛ), специалист по космической радиосвязи Дж. Пирс, специалист по радиоавтоматике Г. Боде, изобретатели транзисторов Лауреаты Нобелевской премии У. Шокли, Дж. Бардин и У. Браттейн, изобретатель релейного компьютера Г. Стибиц и многие другие. И хотя отдельные специалисты в различных странах мира вносили существенный вклад в развитие математической теории связи, однако научный климат Белловских телефонных лабораторий содействовал тому, что именно специалисты БТЛ создали прикладную теорию информации (см. Прил. 2).

С появлением радиосвязи (А. С. Попов – 1895 г., Г. Маркони – 1896 г.) воз-никли дополнительные теоретические проблемы.

В 1915 г. американский радиофизик Дж. Карсон (1886-1940) предложил метод амплитудной модуляции с одной боковой полосой, что увеличивает производительность радиосвязи почти вдвое.

В 1922 г. тот же Карсон провёл математический анализ метода частотной модуляции.

В 1928 г. Гарри Найквист изобрёл фазовую манипуляцию; однако прошло более 40 лет, прежде чем фазовая манипуляция была реализована и получила широкое применение в современных системах электросвязи.

В 1928 г. тот же Найквист определил предельно возможную скорость телеграфирования по проводным линиям с ограниченной полосой пропускания.

В 1932 г. советский инженер Владимир Котельников (1908-2005) сформулировал и доказал теорему отсчётов теории сигналов.

В статьях Клода Шеннона 1940 г. ([46], с. 433-460; опубликована эта статья лишь после Второй мировой войны) и 1948 г. ([46], с. 243-332) прикладная теория информации получила фундаментальные математические основы.

В 1940 г. К. Шеннон написал статью «Связь при наличии шума» (хотя статья была опубликована лишь в 1949 г., сотрудники БТЛ должны были знать её содержание), в которой он впервые предлагает метод «геометрического представления сигналов и помех» в системах телеграфной и телефонной связи, а также в радиовещании, на основании которого он выводит ряд результатов общей теории связи, то есть прикладной теории информации.

Во-первых, при построении метода геометрического представления сигналов Шеннон «переоткрывает» теорему В. А. Котельникова (1932 г. – [21]) и приводит её доказательство, аналогичное доказательству Котельникова, а перед доказательством замечает ([46], с. 435): «Это общеизвестный в теории связи [видимо, среди специалистов БТЛ – Г. Х.] факт».

Во-вторых, он неосторожно утверждает ([46], с. 436-437): «... любая функция, ограниченная полосой W и временным интервалом T, может быть полностью определена заданием 2 T W чисел».

Следуя Найквисту и Ральфу Хартли, К. Шеннон принимает логарифмическую меру количества информации в сообщении, но с учётом не-равноверо-ятности этих сообщений, и определяет пропускную способность электрического или радиоканала связи как C = W log₂[(P + N )/N ], где W – полоса пропускания канала связи, P – мощность сигнала, N – средняя мощность теплового «белого шума». К сожалению, в доказательстве этой важной формулы имеется существенное противоречие: если сигнал s(t) имеет финитное преобразование Фурье: 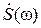= 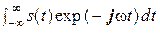, где = 0 при – 2 π W ≤ ω ≤ 2 π W, – то он должен иметь бесконечную длительность T, ограниченную энергию 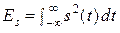и, следовательно, – бесконечно малую мощность: .

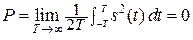Наконец, он доказывает следующую теорему ([46], с. 447): «Применяя достаточно сложную систему кодирования, можно передавать двоичные цифры

со скоростью C = W log₂[(P + N )/N ] со сколь угодно малой частотой ошибок». Тем самым наметился подход к решению исторических Проблем №3 и №4.

В 1948 г. выходит в свет фундаментальная статья К. Шеннона «Математическая теория связи» ([46], с. 243-332). В этой статье Шеннон, отмечая важность работ Найквиста 1924 и 1928 гг. [53, 54] и Хартли 1928 г. [50], ставит своей целью ([46], с. 243) расширить теорию «... с тем, чтобы включить ... влияние шума в канале и возможность экономии за счёт учёта статистической структуры исходного сообщения и назначения передаваемой информации».

Вначале Шеннон вводит пропускную способность C дискретного канала

связи без помех как

,

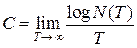где N(T ) – число допустимых сигналов длительностью T.

Затем он учитывает частотность и статистическую взаимозависимость (на основе теории Марковских цепей) появления букв в английских текстах.

В теореме 2 Шеннон вводит понятие энтропии как меры количества информации, выдаваемой источником дискретных сообщений (ДИС), совместную энтропию двух множеств сообщений и условную энтропию одного множества по отношению к другому, а также рассматривает свойства различных источников ДИС и операции кодирования и декодирования как переход входного и выходного преобразователей символов с памятью из одного состояния в другое под воздействием приходящих на преобразователи символов.

Наконец он формулирует основную теорему для канала без помех, предлагает метод кодирования для снятия избыточности ДИС и корректно отмечает, что этот же метод кодирования независимо от него нашёл Роберт Фано (род. в 1917 г.). Тем самым К. Шеннон даёт ключ к решению Проблем №1 и №2.

Далее Шеннон рассматривает канал с помехами, вводит понятие остаточной неопределённости (equivocation) на выходе канала связи, доказывает основную теорему для дискретного канала с помехами и приводит пример помехоустойчивого канального кодирования: код Ричарда Хэмминга (1915-1998). Это – «черновое решение» Проблемы №5.

Затем К. Шеннон переходит к информационным свойствам «непрерывных сообщений» и каналов связи. Здесь он снова формулирует (уже без доказательства) теорему отсчётов и соответствующий геометрический метод представления сигналов в линейном пространстве 2 T W измерений. Энтропию «непреры-вного распределения» он определяет, по аналогии с источниками дискретных сообщений, как .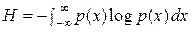

Далее Шеннон рассматривает пропускную способность «непрерывного канала» и определяет её как C = W log₂[(P + N )/N ], где P – средняя мощность передаваемых сигналов, N – средняя спектральная плотность мощности «белого шума». Он также корректно ссылается на аналогичные результаты Н. Винера (1948 г.) и У. Таллера (1949 г.). Результат Шеннона явился абстрактно-матема-тическим решением Проблем №3 и №4.

Потом Шеннон определяет производительность источника непрерывных сообщений при заданной точности их воспроизведения и приводит оценки её границ для произвольного источника.

Самым выдающимся новшеством К. Шеннона, по-видимому, следует считать математическое определение остаточной неопределённости(equivocation) на выходе канала связи с помехами, которое позволяет оценивать информационные потери, сопровождающие передачу сообщений по каналам связи при наличии в каналах связи различного рода помех – и даёт ключ к решению исторической Проблемы №5. Остальные идеи в это время просто «носились в воздухе» и открывались независимо от Шеннона (В. А. Котельников, У. Беннетт, Д. Габор, Р. Фано, У. Таллер и др.).

Отдельные существенные результаты прикладной теории информации были получены независимо от сотрудников БТЛ разными учёными в различных

странах мира. Восемью годами ранее Шеннона советский инженер В. А. Котельников сформулировал и доказал знаменитую теорему отсчётов для сигналов с финитным спектром, а также вывел из неё ряд важных практических следствий.

Однако благодаря сложившимся творческим традициям учёных БТЛ и незаурядной математической интуиции К. Шеннона последнему удалось, по существу в одной публикации, синтезировать весь основной комплекс математических проблем теории связи и подходов к их решениям. Правда, Шеннон не избежал недоразумений как по содержанию (в части информационной меры «непрерывных сообщений»), так и по форме (в части аналогий с термодинамикой).

С другой стороны, одним из недостатков работ К. Шеннона по теории ПТИ следует считать отсутствие чёткого разделения прикладной теории информации на информационную статику и информационную динамику. Поэтому у Шеннона зачастую не ясно, относится ли данная теорема, например, к любым «запоминающим устройствам» или же только к динамическим каналам связи без накопителей информации.

Статья К. Шеннона 1948 г. была замечена как инженерами, так и математиками. О содержании ещё не опубликованной статьи Шеннона 1940 г. знали, по-видимому, в Великобритании, в которой, в силу военных обстоятельств, проводились обширные научно-исседовательские и опытно-конструкторские работы в области радиолокации. В Великобританском «НИИ дальней связи» (“Telecommunications Research Establishment” – TRE; организован в мае 1940 г.) Филип Вудворд (род. в 1919 г.) и И. Дейвис проводили теоретические исследования в области военной радиолокации, результаты которых были представлены правительству Великобритании в научно-техническом отчёте в 1948 г.

А уже в 1953 г. Ф. Вудворд публикует монографию «Теория вероятностей и теория информации с применениями в радиолокации» (см. [12]), в которой

он, наряду со своими оригинальными идеями, развивает информационный подход К. Шеннона применительно к радиолокации.

Радиоинженеры продолжали совершенствовать методы модуляции. В 1960 г. американский изобретатель К. Кан (C. R. Cahn) предложил квадратурную амплитудную модуляцию (QAM ), которая имеет число дискретных сигнальных позиций от 16 до 256 и которая имеет скорость передачи информации, при прочих равных условиях, почти в два раза бóльшую, чем классические аналоговые способы модуляции (см. разд. 17). Математический анализ модуляции QAM провёл американский учёный Роберт Галлагер (род. в 1931 г.).

Математики не восприняли всерьёз Шеннона как математика. Так, например ([5], с. 293), «... крупный американский специалист в области теории вероятностей Дж. Л. Дуб в своей рецензии на работу К. Шеннона отмечал, что она целиком основана на эвристических предположениях и не содержит ни одного математически строго доказанного результата».

Одним из первых математическую значимость работ К. Шеннона оценил советский математик А. Н. Колмогоров (1903-1987). В предисловии к сборнику переводов работ К. Шеннона Колмогоров отмечает ([46], с. 5): «Правда, строгое математическое “обоснование” своих идей Шеннон … предоставил своим продолжателям. Однако его математическая интуиция изумительно точна».

После небольшого периода непонимания К. Шеннона математиками в 1950-х годах его идеи получили существенное развитие в рамках математической (формальной) теории информации (МТИ). В теории МТИ сформировалось два направления.

Одно из них связано с математическим обоснованием и совершенствованием общих теорем теории МТИ, с методами аналитической оценки пропускной способности различных каналов связи и вычисления информационной надёжности передачи сообщений при наличии в каналах связи различного рода ограничений [5, 13, 14, 18, 33, 34] (Проблемы №3,№4и№5: А. Н. Колмогоров,

А. Я. Хинчин, Р. Л. Добрушин, М. С. Пинскер – СССР; Б. МакМиллан, А. Файн-стейн, Дж. Вольфовиц, Р. Галлагер – США и др.).

Второе направление МТИ связано с разработкой оптимальных методов кодирования источников дискретных и «непрерывных» сообщений с целью снятия естественной избыточности источников информации (Проблемы №1 и №2), а также канального (помехоустойчивого, избыточного) кодирования и декодирования (Проблема №5). В 1950 г. американский математик Ричард Хэмминг (1915-1998) развил математические основы блочного кодирования. Дэвид Слепян (1923-2007) применил алгебраическую теорию групп для анализа и синтеза блочных кодов. Тем самым теория помехоустойчивого кодирования получила для своего развития прочный математический фундамент.

Основные этапы развития теории кодирования см. в Прил. 3.

Наряду с математической теорией информации в 1950-60-х гг. методики К. Шеннона стали применяться в самых различных областях знаний, стимулируя тем самым развитие различных прикладных теорий информации.

В настоящем пособии мы будет иметь в виду одну из многочисленных прикладных теорий информации: применение математической теории информации к системам электро- и радиосвязи (информационная теория радиотехнических систем). Поэтому следует упомянуть об истории развития (также на основе теории вероятностей и математической статистики) теоретической метрологии [36, 47], которая имеет дело с информационными эрготехническими («человеко-машинными») системами, формирующими (вырабатывающими) информацию.

В 1794 г. французский математик Адриен Лежандр (1752-1833) и немецкий Карл Гаусс (1777-1855) разработали метод наименьших квадратов и оценили дисперсию выборочного среднего и выборочного среднеквадратического отклонения в выборке из нормальной генеральной совокупности.

Независимо от них аналогичный метод разработал американский математик Роберт Эдрейн (1775-1843).

В 1894 г. английский статистик Карл Пирсон (1857-1936) предложил метод моментов в качестве общего метода нахождения оценок параметров функций распределения вероятностей по выборочным данным, а в 1900 г. – критерий χ² («хи-квадрат»).

В 1912 г. английский статистик Рональд Фишер предложил метод максимального правдоподобия, в ходе разработки которого в 1921 г. он ввёл понятие информационной матрицы (см. Введение).

В 1937 г. российско-польско-американский математик Ежи Нейман (1894-1981) развил теорию интервального оценивания (не путать с известным венгеро-американским физиком-теоретиком Джоном (Яношем) фон Нейманом: 1903-1957 – который в 1949 г. предложил метод Монте-Карло!).

Всё это также оказывало влияние на развитие прикладной теории информации применительно к теоретической радиотехнике.

Кроме того, для технических применений были разработаны математические модели, адекватные различным помехам и шумам в каналах связи.

В 1909 г. английский физик и философ Норман Кэмпбелл (1880-1949: не путать с американским математиком Г. Кэмпбеллом, работавшим в БТЛ!) при изучении фотоэлектрической эмиссии разработал математическую модель тока

эмиссии i(t) в виде суммы импульсов f (t) [20]: 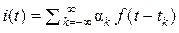, где α_k – случайные коэффициенты, а t_k – случайные моменты времени, и сформулировал основные свойства этой модели (теорема Н. Кэмпбелла).

В 1925 г. уже упоминавшийся американский радиофизик Дж. Карсон использовал аналогичную модель для описания атмосферных флуктуационных радиопомех («статиков») и позже доказал теорему: процесс ξ(t) имеет спектр мощности, пропорциональный квадрату модуля преобразования Фурье функции f (t) – теорема Карсона [49].

В 1928 г. Г. Найквист в статье [55], на основании экспериментальных работ Дж. Джонсона, теоретически оценил спектральную плотность средней мощ-ности тепловых электрических шумов резисторов (формула Найквиста-Джон-сона).

В 1932 г. Г. Найквист показал, что модель радиопомех Карсона в предельном случае гауссовских шумов эквивалентна совокупности синусоид со случайными амплитудами и фазами.

В 1934 г. американский математик Норберт Винер (1894-1964) и советский математик Александр Яковлевич Хинчин (1894-1959) – последний: на основании работ по случайным процессам российско-советского математика, статистика и экономиста Евгения Евгеньевича Слуцкого (1880-1948) – заложили основы спектрально-корреляционной теории стационарных случайных сигналов (теорема Винера-Хинчина).

В 1939 г. А. Н. Колмогоров развил теорию предсказания и оптимальной фильтрации случайных процессов [17] (аналогичные результаты Н. Винер получил в 1942-48 гг. [59]).

В фундаментальной работе 1944/45 гг. [56] Стефена Райса (1907-1986) теория случайных шумов имеет уже вполне современный вид.

И, наконец, необходимо иметь в виду ещё одну область знаний, которая определяет современный облик общей теории информации: в процессе исторического развития логико-математических работ немецкого философа, математика, физика и языковеда Готфрида Лейбница (1646-1716) выросла наука о знаковых системах в живой природе и в обществе – семиотика («знаковедение») [28, 30]. Одним из первых её разработчиков был американский философ и логик Чарльз Пирс ([25]: 1839-1914), который развил основные положения теории знаков. Его последователь американский семиотик Чарльз Моррис (1901-1978: [30]) подразделил общую семиотику на синтактику («структуроведение»), семантику («смысловедение») и прагматику («пользоведение») (см. Прил. 1).

К настоящему времени синтактика развилась в абстрактную (математическую) семиотику, семантика – в биосемиотику, прагматика – в этносемиотику.

Таким образом, историческое развитие технических средств телекоммуникаций и соответствующих им информационных эрготехнических систем (ЭТС) определило совокупность проблем, решаемых в информационной теории радиотехнических систем, и подразделение её на две части:

• информационную статику,которая рассматриваетметоды оптимального и помехоустойчивого кодирования знаковых сообщений, методы оптимального квантования, или округления, а также методы оценивания информативности результатов измерений скалярных величин;

• информационную динамику, которая имеет дело с разработкой методов максимизации скорости передачи информации по различным каналам электросвязи, работающих в режиме реального времени, методов оценивания скорости передачи измерительной (метрологической) и знаковой (семиотической) информации по каналам электросвязи при наличии в них различного рода помех.

Выявив историческую логику развития прикладной теории информации, перейдём к формально-логическому её построению.

Однако перед тем как приступить к систематическому изложению основ теории ПТИ, отметим, что ключевое понятие «информация» и соответствующие ему прикладные теории информации получили самое разнообразное развитие и применение: от узкотехнического (как основа теории устранения информационной избыточности источников сообщений и помехоустойчивого кодирования различных сигналов в каналах электросвязи при наличии в них помех – К. Шеннон [46]) – до неоправданно широкого (например, «фундаментальная» теория связи и управления в живой и неживой природе – Н. Винер [10]). Претензии Винера на общефилософскую обобщённость понятия «информация» в рамках науки «кибернетика» не оправдались, поскольку информационное взаимодействие – в живой природе и взаимодействие элементов автоматизиро-ванных подстстем управления – в эрготехнических информационно-управля-ющих системах имеют принципиально различные закономерности. Эти закономерности, хотя и обладают некоторым формально-математическим сходством, но изучаются в различных областях знаний и различными экспериментально-теоретическими методами: первая – в науке о биологических сообществах, вторая – в теории систем автоматического управления (САУ). Поэтому следует согласиться с Дж. Пирсом, который ещё в 1962 г. в своей монографии «Символы, сигналы, шумы. Закономерности и процессы передачи информации» (которую рецензировал сам К. Шеннон!), написал ([24], с. 266): «К счастью, … лишь немногие учёные признают себя кибернетиками, да и то в разговоре с теми, кого они считают безнадёжно отсталыми».

Однако многочисленные последователи Н. Винера довели его идеи до абсурдного логического завершения. Например, в так называемой «радиоинформатике» ([19], c. 2): «Информация обосновывается как физическая величина, на которую распространяются законы сохранения, пространственно-временнáя метрика, мера и система размерностей, присущие косной и живой природе».

А в «науке», которую авторы монографии [22] назвали информодинамикой, мы, якобы, «… имеем дело с некоторой сущностью, во многом похожей на электромагнитное поле – некоторым динамическим структурным полем ( ДСП) и информационной машиной как его резонатором» (с. 296). При этом структурное взаимодействие в ДСП (с. 302) «… при определённых условиях, “сворачивается в ДСП”, а затем, “в большом Взрыве” [кавычки авторов работы [22] – Г. Х.], разворачивается в структуру, обеспечивающую единство энергетической и информационной половинок Вселенной и является структурой для каждой из этих половинок и всего вместе как целого». На с. 303 монографии [22] эти утверждения завершаются следующим образом: «… остаётся Ему [?! – Г. Х.] только заботиться о её равновесии и поддержании в порядке».

Основные понятия общей (семиотической, «смысловой») теории информации даны в Прил. 1, с которым полезно ознакомиться перед изучением основ информационной теории радиосистем.

Относительно общего понятия «информация» мы будем придерживаться «умеренной» точки зрения:

Эти сообщения могут формироваться (вырабатываться), храниться, обрабатываться, преобразовываться и передаваться посредством знаковых систем различных видов (без потери информации или с её потерями, вызванными различного рода помехами) или непосредственно использоваться субъектами в процессе их информационного взаимодействия.

Вопросы для самопроверки

1. В чём состоит Проблема №1 прикладной теории информации?

2. В чём состоит Проблема №2 прикладной теории информации?

3. В чём состоит Проблема №3 прикладной теории информации?

4. В чём состоит Проблема №4 прикладной теории информации?

5. В чём состоит Проблема №5 прикладной теории информации?

6. Какова роль Александра Белла в создании прикладной теории информации?

7. Каково основное содержание фундаментальных статей 1940 и 1948 гг. Клода Шеннона, и какие проблемы математической теории электросвязи в них решаются?

8. Какие направления математической теории информации получили наибольшее развитие?

9. Каковы области знаний, которые примыкают и частично перекрываются информационной теорией радиосистем?

10. Что такое семиотика, и на какие области она подразделяется?

11. Каково определение понятия «информация» в прикладной теории информации?