Кодирование Шеннона-Фано и Хаффмена
Пусть на входе подсистемы ПСППС (рис. 1: во входном преобразователе 1 или сразу же после него) имеется кодирующее устройство, которое каждому поступающему от источника ДИС знаку uj  U,U = {uj}
U,U = {uj}  , по определённым правилам ставит в соответствие кодовое слово
, по определённым правилам ставит в соответствие кодовое слово 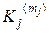 = (vj1, vj2, …, vjl, …,
= (vj1, vj2, …, vjl, …, 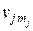 ) длиной mj, которое состоит из mj символов vjl, взятых из совокупности V = = {vl; l = 1, …, M } (кодер источника сообщений). При этом, естественно, M ≤ N. Этот процесс называется кодированием источника ДИС.
) длиной mj, которое состоит из mj символов vjl, взятых из совокупности V = = {vl; l = 1, …, M } (кодер источника сообщений). При этом, естественно, M ≤ N. Этот процесс называется кодированием источника ДИС.
Если 2 ≤ M << N, а все Pj ( j = 1, 2, …, N ) – различны, то можно так закодировать сообщения {uj}  (с помощью последовательностей
(с помощью последовательностей 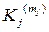 , то есть кодовых слов из множества
, то есть кодовых слов из множества 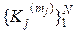 = K), что в длинной последовательности элементарных сообщений Si(n) = ( ui1, ui2, …, uik, …, uin ); n → ∞; частотность pr появления символа vr в любой закодированной последовательности Si(n) = ( ui1, ui2, …, uik, …, uin ) будет асимптотически стремиться к величине 1/M, то есть
= K), что в длинной последовательности элементарных сообщений Si(n) = ( ui1, ui2, …, uik, …, uin ); n → ∞; частотность pr появления символа vr в любой закодированной последовательности Si(n) = ( ui1, ui2, …, uik, …, uin ) будет асимптотически стремиться к величине 1/M, то есть
«вторичный источник сообщений», образованный входным
преобразователем и кодером источника ДИС, будет обладать
максимальным количеством информации на один символ
из совокупности V = {vl} 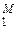 : :  (V) ≡ H(V) = Hмакс = log M. (V) ≡ H(V) = Hмакс = log M.
|
Чтобы добиться этого, нужно, чтобы в каждом разряде (l-й позиции) кодовых слов uj = (vj1, vj2, …, vjl, …, 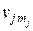 ) вероятности появления символов vl были бы по возможности одинаковыми. Разделим множество U = {uj}
) вероятности появления символов vl были бы по возможности одинаковыми. Разделим множество U = {uj}  на M групп таким образом, чтобы суммарная вероятностьзнаков {uj} в каждой группе была бы по возможности одинаковой и близкой к величине 1/M. Припишем каждому знаку из этих групп в «первом разряде» кодового слова
на M групп таким образом, чтобы суммарная вероятностьзнаков {uj} в каждой группе была бы по возможности одинаковой и близкой к величине 1/M. Припишем каждому знаку из этих групп в «первом разряде» кодового слова 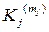 один из символов множества V = {vl}
один из символов множества V = {vl} 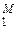 .
.
Ясно, что при n → ∞ в сообщении Si(n) = ( ui1, ui2, …, uik, …, uin ) в первом разряде кодовых слов uj = ( vj1, …, vjl, …, 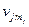 ) символ vl будет появляться с частотностью pl ≈ 1/M.
) символ vl будет появляться с частотностью pl ≈ 1/M.
Разобьём каждую из полученных выше M групп на M подгрупп так, чтобы суммарная вероятность каждой подгруппы имела бы величину около M –2, и припишем «второму разряду» кодовых слов один из символов vl (l = 1, …, M ). Этот процесс будем продолжать до тех пор, пока число знаков в последней подгруппе станет не более величины M. В этом последнем разбиении в «последнем разряде» кодовых слов запишем один из символов vl (l = 1, …, M ).
Что же в результате таких построений получается? В любом из закодированных сообщений Si(n) при n → ∞ частотность pl любого из символов {vl} 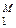 приблизительно одна и та же и равна pl ≈ 1/M. Поскольку все знаки {uj}
приблизительно одна и та же и равна pl ≈ 1/M. Поскольку все знаки {uj}  – независимы, то при указанном способе кодирования также независимы и все символы {vl}
– независимы, то при указанном способе кодирования также независимы и все символы {vl} 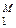 . Значит, каждый из символов vl
. Значит, каждый из символов vl 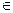 V будет нести приблизительно одинаковое количество информации Iv, равное Iv = log M. Для знака uj понадобится столько символов из множества V, чтобы Ij ≈ mj Iv. Отсюда следует, чтодлинаmjкодового слова
V будет нести приблизительно одинаковое количество информации Iv, равное Iv = log M. Для знака uj понадобится столько символов из множества V, чтобы Ij ≈ mj Iv. Отсюда следует, чтодлинаmjкодового слова 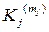 для j-го знакаuj есть mj ≈ Ij / Iv = – log Pj / log M.
для j-го знакаuj есть mj ≈ Ij / Iv = – log Pj / log M.
Фактическая средняя длинакодового слова равна mср= 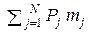 , атео-
, атео-
ретическая(минимально возможная):
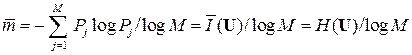 (символ/знак).
(символ/знак).
При этом mср ≥ 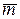 .
.
Таким образом, мы доказалитеорему Шеннона о кодировании источника дискретных сообщений (теорема об устранении избыточности источника
ДИС, или теорема о сжатии данных):
если имеется источник независимых знаковых сообщений {U, P, I, S},
то совокупность элементарных сообщений (знаков)U = {uj}  можно закодировать посредством совокупности символов V = {vl}
можно закодировать посредством совокупности символов V = {vl} 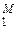 таким образом, чтобы средняя длина кодового слова mср
была минимально возможной и лежать в пределах
[
таким образом, чтобы средняя длина кодового слова mср
была минимально возможной и лежать в пределах
[ 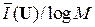 ] ≤ mср ≤ [ ] ≤ mср ≤ [ 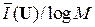 + 1].
Точное равенство mср= + 1].
Точное равенство mср= 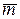 = = 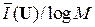 имеет место
у тех источников ДИС, у которых для любого ujвыполняется
точное равенство:– log Pj = mj log M, где mj– целое число, то есть
все величины log Pj ( j = 1, 2, …, N ) делятся на величину log M нацело. имеет место
у тех источников ДИС, у которых для любого ujвыполняется
точное равенство:– log Pj = mj log M, где mj– целое число, то есть
все величины log Pj ( j = 1, 2, …, N ) делятся на величину log M нацело.
|
Такое кодирование сообщений источников ДИСназываетсяоптимальным по средней длине кодового слова. Эта теорема решает историческую Проблему №2 прикладной теории информации (см. разд. 1).
Примером кодирования источника дискретных сообщений в случае M = 2 (V= {v1, v2} – двоичный код) является алгоритм Шеннона-Фано. В качестве иллюстрации приведём его реализацию при N = 9. В данном случае
U = {u1, u2, …, uj, …, u9},
P = {0,25; 0,08; 0,13; 0,10; 0,07; 0,25; 0,06; 0,04; 0,02}.
Запишем решение задачи оптимального кодирования такого источника сообщений с помощью двух символов {v1 = 1, v2 = 0} в виде следующей таблицы (табл. 1).
Средняя длина кодового слова mср в данном примере равна:
mср = 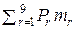 , или
, или
mср = 0,35·2 + 0,15·2 + 0,13·3 + 0,10·3 + 0,08·4 + 0,07·4 + 0,06·4 + 0,04·5 + 0,02·5,
то есть mср = 2,83 (символ/знак).
Теоретически возможная средняя длина
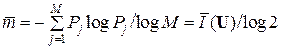 , или
, или
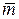 = 0,35·1,517 + 0,15·2,735 + 0,13·2,943 + 0,1·3,322 + 0,08·3,644 + 0,07·3,837 +
= 0,35·1,517 + 0,15·2,735 + 0,13·2,943 + 0,1·3,322 + 0,08·3,644 + 0,07·3,837 +
+ 0,06·4,059+ 0,04·4,644 + 0,02·5,644,
то есть 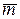 = 2,76 (символ/знак). Как видим,
= 2,76 (символ/знак). Как видим, 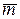 < mср. Удельная информативность данного источника ДИС
< mср. Удельная информативность данного источника ДИС  (U) ≡ H(U) = 2,76 бит/знак, а его коэффициент избыточности η(U) = 1 –
(U) ≡ H(U) = 2,76 бит/знак, а его коэффициент избыточности η(U) = 1 – 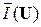 / log N = 1 – 2,76/log 9 = 0,129.
/ log N = 1 – 2,76/log 9 = 0,129.
Таблица 1
Способ кодирования Шеннона-Фано
| r | ur | Pr | Ir бит | Разряды кодового слова | Фактич. длина mr | ||||
| u1 | 0,35 | 1,517 | – | – | – | ||||
| u6 | 0,15 | 2,735 | – | – | – | ||||
| u3 | 0,13 | 2,943 | – | – | |||||
| u4 | 0,10 | 3,322 | – | – | |||||
| u2 | 0,08 | 3,644 | – | ||||||
| u5 | 0,07 | 3,837 | – | ||||||
| u7 | 0,06 | 4,059 | – | ||||||
| u8 | 0,04 | 4,644 | |||||||
| u9 | 0,02 | 5,644 | |||||||
| ΣPr = 1 |
Это значит, что для передачи (записи в ПЗУ) того же самого количества информации, содержащейся в сообщении Si(n) 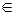 S, можно было бы обойтись семью знаками {uj}
S, можно было бы обойтись семью знаками {uj}  (теоретически 6,8: log N0 = 2,76; N0 = 6,8).
(теоретически 6,8: log N0 = 2,76; N0 = 6,8).
Покажем, что любая бинарная последовательность декодируется однозначно. Например, последовательность 101000111100000… по Шеннону-Фано
декодируется как u6, u6, u2, u1, u9, …
После кодирования по Шеннону-Фано вторичный источник сообщений «ДИС+Кодер» имеет коэффициент избыточности ηШФ = 1 – H(U)/mср = 0,042, то есть по сравнению с первичным источником ДИС уменьшился почти в три раза.
Спрашивается, а какова предельно достижимая минимальная остаточная избыточность при бинарном кодировании данного источника ДИС?
На этот вопрос конструктивно ответил Дэвид Хаффмен (см. разд. 1 и Прил. 5).
Чтобы показать, что алгоритм бинарного кодирования, предложенный Хаффменом, является оптимальным по критерию минимальной средней длины кодовых слов, введём понятие «префиксные коды». Для этого возьмём два кода, имеющие следующую таблицу соответствия.
| Сообщение | u1 | u2 | u3 | u4 |
| Код 1 | ||||
| Код 2 |
Можно убедиться, что последовательность 011100110010… в соответствии с кодом 1 однозначно не декодируется, а с кодом 2 декодируется однозначно: u1, u4, u1, u1, u3, u1 u2. Как можно заметить, в коде 2 кодовые слова не являются началами других кодовых слов, и поэтому при декодировании не возникает путаницы. Коды, у которых ни одно кодовое слово не является началом другого, называются префиксными.
Если мы имеем некоторый источник ДИС, то согласно теореме кодирования Шеннона средняя длина кодовых слов для него лежит в пределах:
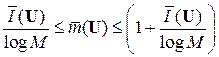 .
.
При M = 2: 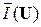 ≤
≤ 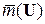 ≤ [1 +
≤ [1 + 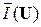 ].
].
Код Шеннона-Фано не является оптимальным, как показал в 1950 г. аспирант Роберта Фано Дэвид Хаффмен, который и предложил алгоритм оптималь-
ного бинарного кодирования.
Итак, пусть, как и при кодировании по Шеннону-Фано, сообщения uj ( j = 1, 2, …, N ) источника ДИС U = {uj}  пронумерованы в порядке невозрастания их априорных вероятностей: P1 ≥ P2 ≥ … ≥ Pj ≥ … ≥ PN.
пронумерованы в порядке невозрастания их априорных вероятностей: P1 ≥ P2 ≥ … ≥ Pj ≥ … ≥ PN.
Если бинарный код источника ДИС U = {uj}  = {
= { 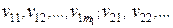 ,
,
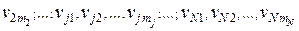 } оптимальный, то есть имеет наименьшую среднюю длину
} оптимальный, то есть имеет наименьшую среднюю длину 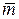 кодовых слов
кодовых слов 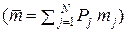 , то длины слов не убывают: m1 ≤ m2 ≤ … ≤ m j ≤ … ≤ mN.
, то длины слов не убывают: m1 ≤ m2 ≤ … ≤ m j ≤ … ≤ mN.
Докажем это. Пусть при j < l величина m j больше m l. Заменим j-е слово l-м и наоборот. Средняя длина 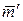 кодовых слов при этом окажется равным:
кодовых слов при этом окажется равным: 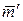 =
= 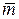 –
– 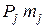 –
– 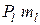 +
+ 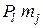 +
+ 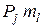 =
= 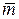 – (m j – ml) (Pj – Pl) <
– (m j – ml) (Pj – Pl) < 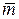 . Полученное противоречие доказывает наше утверждение.
. Полученное противоречие доказывает наше утверждение.
Значит, наименее вероятное сообщение из ансамбля U = {uj}  имеет наибольшую длину. Это почти очевидно.
имеет наибольшую длину. Это почти очевидно.
Далее. В оптимальном двоичном префиксном коде всегда имеются два кодовых слова, имеющие одну и ту же максимальную длину, отвечающие двум наименее вероятным элементарным сообщениям из ансамбля U = {uj}  и отличающиеся только последним символом.
и отличающиеся только последним символом.
Доказательство. Предположим, что такое кодовое слово только одно и имеет длину mмакс. Поскольку ни одно из остальных кодовых слов не является префиксом (началом) этого слова (максимальной длины), то его не нужно отличать от ему подобного. Значит, можно последний символ (“ноль” или “единицу”) безболезненно отбросить. Но тогда длина его станет (mмакс – 1), а средняя длина кодовых слов – уменьшится. А это противоречит оптимальности кода.
Пусть, напротив, имеются три кодовых слова наибольшей длины mмакс.
Тогда одно из них в качестве последнего символа имеет “единицу”, а два других – “ноль” (или наоборот). Но тогда одно из двух оставшихся кодовых слов должно отличаться другими символами. Значит, последний символ у этого кодового слова можно отбросить и условие однозначного декодирования от
этого не нарушится, поскольку исходный код был префиксным.
Следовательно,
| оптимальный бинарный префиксный код обязательно имеет пару кодовых слов максимальной длины, последними символами которых являются “ноль” и “единица”. |
Отсюда практический вывод: оптимальное бинарное кодирование нужно начинать не сверху, как в алгоритме Шеннона-Фано, а снизу. То есть нужно взять знаки из ансамбля U = {uj}  с наименьшими вероятностями, поставить в качестве последнего символа их кодовых слов соответственно “ноль” и “единицу” и вычислить априорную вероятность появления сложного сообщения, заключающегося в появлении в тексте одного из них. Поскольку сообщения u j ( j = 1, 2, …, N ) независимы, то эта вероятность равна сумме вероятностей двух знаков с наименьшими априорными вероятностями. Затем следует объединить последние два сообщения в одно (с различными последними символами), и полученный ансамбль из N – 1 элементарных и одного сложного сообщения снова расположить в порядке невозрастания их априорных вероятностей, снова найти два наименее вероятных сообщения (а они, по доказанному выше, должны быть!), приписать им в качестве последних символов “ноль” и “единицу” и снова объединить их в одно сложное сообщение – и так далее. Пока у нас не останется два сообщения, для которых в первом разряде их кодовых слов следует записать “ноль” и “единицу” соответственно.
с наименьшими вероятностями, поставить в качестве последнего символа их кодовых слов соответственно “ноль” и “единицу” и вычислить априорную вероятность появления сложного сообщения, заключающегося в появлении в тексте одного из них. Поскольку сообщения u j ( j = 1, 2, …, N ) независимы, то эта вероятность равна сумме вероятностей двух знаков с наименьшими априорными вероятностями. Затем следует объединить последние два сообщения в одно (с различными последними символами), и полученный ансамбль из N – 1 элементарных и одного сложного сообщения снова расположить в порядке невозрастания их априорных вероятностей, снова найти два наименее вероятных сообщения (а они, по доказанному выше, должны быть!), приписать им в качестве последних символов “ноль” и “единицу” и снова объединить их в одно сложное сообщение – и так далее. Пока у нас не останется два сообщения, для которых в первом разряде их кодовых слов следует записать “ноль” и “единицу” соответственно.
Для оптимального кодирования по Хаффмену очень удобно пользоваться «кодовым деревом», состоящим из узлов и ветвей. Каждые две ветви заканчиваются узлом. Одной ветви данного узла приписывается “единица” (например,
верхней), а другой (например, нижней) – “ноль”.
Рассмотрим для наглядности пример кодирования по Хаффену источника ДИС, который мы закодировали по Шеннону-Фано (см. табл. 2).
| Кодовое слово | Факт. длина | ur | Pr |
| u1 | 0,35 | ||
| u6 | 0,15 | ||
| u3 | 0,13 | ||
| u4 | 0,10 | ||
| u2 | 0,08 | ||
| u5 | 0,07 | ||
| u7 | 0,06 | ||
| u8 | 0,04 | ||
| u9 | 0,02 | ||
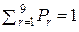
|

 1
1



 1 0,63 1
1 0,63 1



 1 0,37 0 вход
1 0,37 0 вход



 1 0,28 0
1 0,28 0

 1 0 0
1 0 0




 0 0,15 0,22
0 0,15 0,22

 1 0
1 0


 1 0 0,12
1 0 0,12

 0 0,06
0 0,06
Как видим, в данном конкретном случае код Шеннона-Фано и Хаффмена эквивалентны, то есть большего сжатия сообщений не получить – при бинарном кодировании первичных знаков.
Проверим префиксность (однозначность декодирования) кода Хаффмена:
100111001111101… = u2, u1, u4, u1, u1, u6,…
Таким образом, в разд. 4 мы рассмотрели понятие «удельная информативность  (U)» (бит/знак) данного источника ДИС, возможность очень простого оценивания с её помощью количества информации, которое содержится в любом достаточно длинном сообщении Si(n), производимом данным источником ДИС: I(Si(n)) ≈ n
(U)» (бит/знак) данного источника ДИС, возможность очень простого оценивания с её помощью количества информации, которое содержится в любом достаточно длинном сообщении Si(n), производимом данным источником ДИС: I(Si(n)) ≈ n  (U), понятие «коэффициент информационной избыточности» η(U) источника ДИС и возможность количественного сравнения различных способов кодирования статических источников ДИС.
(U), понятие «коэффициент информационной избыточности» η(U) источника ДИС и возможность количественного сравнения различных способов кодирования статических источников ДИС.
Построили также оптимальный алгоритм бинарного кодирования источника ДИС, позволяющий минимизировать избыточность вторичного источника «ДИС+Кодер». Это решает исторические Проблемы №1 и №2 – оптимальное
кодирование и снятие избыточности источников ДИС (см. разд. 1).
Перейдём к оцениванию потерь информации, происходящей в канале передачи дискретных сообщений.
Вопросы для самопроверки
1. Как минимизировать избыточность источника дискретных сообщений с помощью кодера источника?
2. Какова формулировка теоремы Шеннона о кодировании источника дискретных сообщений?
3. В чём состоит алгоритм кодирования Шеннона-Фано?
4. Что такое префиксные коды?
5. Почему оптимальные бинарные префиксные коды обязательно имеют пару кодовых слов максимальной длины, последними символами которых являются “ноль” и “единица”?
6. В чём состоит алгоритм кодирования Хаффмена?
Дата добавления: 2015-05-16; просмотров: 1381;
