Избыточность источников ДИС
Рассмотрим простейший статический источник знаковых («дискретных») сообщений (ДИС). Математически он представляется информационной моделью {U, P, I, S}, в которой U = {uj}  есть множество неравновероятных независимых элементарных сообщений. Согласно свойству аддитивности информации, количество информации, которое содержится в любой i-й последовательности знаков (в предложении или в тексте) Si(n) = ( ui1, ui2, …, uik, …, uin ), выдаваемой источником ДИС, есть I(Si(n)) =
есть множество неравновероятных независимых элементарных сообщений. Согласно свойству аддитивности информации, количество информации, которое содержится в любой i-й последовательности знаков (в предложении или в тексте) Si(n) = ( ui1, ui2, …, uik, …, uin ), выдаваемой источником ДИС, есть I(Si(n)) = 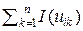 .
.
При достаточно большом значении n (n →∞) каждый из знаков uj множества U = {uj}  будет встречаться в сообщении Si(n) много раз. Если ni j – количество знаков uj, встретившихся в i-м сообщении (тексте) Si(n), то
будет встречаться в сообщении Si(n) много раз. Если ni j – количество знаков uj, встретившихся в i-м сообщении (тексте) Si(n), то
I(Si(n)) = 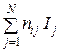 .
.
Если правую часть последнего равенства умножить и разделить на n, то
приближённо(а при n → ∞ – точно) получим
ni j /n ≈ Pj и I(Si(n)) = n 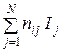 /n ≈ n
/n ≈ n 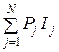 = – n
= – n 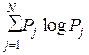 ≡ n
≡ n  (U),
(U),
где  (U) естьсреднее значение количества информации, содержащейся в произвольном знаке u
(U) естьсреднее значение количества информации, содержащейся в произвольном знаке u  U данного источника ДИС, или удельная информатив-
U данного источника ДИС, или удельная информатив-
ность ДИС: 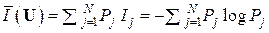 (бит/знак).
(бит/знак).
Величину 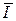 (U) К. Шеннон обозначил как H(U) и не очень удачно назвалэнтропией («неопределённостью») источника ДИС. Энтропия H(U) вычисляется по формуле:
(U) К. Шеннон обозначил как H(U) и не очень удачно назвалэнтропией («неопределённостью») источника ДИС. Энтропия H(U) вычисляется по формуле:
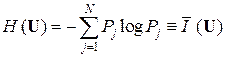 (4.1)
(4.1)
и имеет размерность [H(U)] = бит/знак. К. Шеннон заимствовал термин «энтропия» из статистической механики американского физика-теоретика Дж. Гиббса (1839-1903) из-за аналогии формулы для вычисления энтропии S дискретной термодинамической системы и формулы (4.1), хотя энтропия S имеет иной вероятностный смысл и иную размерность ( Джоуль/оКельвин). Забвение происхождения и смысла формулы (4.1), а также лингвистическая двусмысленность термина «энтропия» привели к большой путанице в понятиях математической теории информации. Поэтому следует согласиться с замечанием (1962 г.) сотрудника по Белловским лабораториям и последователя Шеннона (см. разд. 1) Дж. Пирса ([24], с. 99): «Чтобы понять, что такое энтропия в теории информации, лучше выкинуть из головы всё, что хоть как-то связано с понятием энтропия, применяемым в физике». Поэтому лучше всего величину 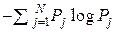 называть удельной информативностью.
называть удельной информативностью.
Итак,
удельная информативность  (U), или энтропия H(U) источника
знаковых («дискретных») сообщений количественнохарактеризует
математическую модель источника ДИС {U, P, I, S}
на синтактическом уровне семиотики. По величине (U), или энтропия H(U) источника
знаковых («дискретных») сообщений количественнохарактеризует
математическую модель источника ДИС {U, P, I, S}
на синтактическом уровне семиотики. По величине  (U) ≡ H(U)
можнообъективносравнивать «информационные мощности»
различных источников ДИС и очень просто оценивать
количество информации I(Si(n)), содержащейся
в любом достаточно длинном сообщении Si(n): I(Si(n)) ≈ n (U) ≡ H(U)
можнообъективносравнивать «информационные мощности»
различных источников ДИС и очень просто оценивать
количество информации I(Si(n)), содержащейся
в любом достаточно длинном сообщении Si(n): I(Si(n)) ≈ n  (U) ≡ n H(U). (U) ≡ n H(U).
|
Можно определить также и дисперсию информативности знаков D(U)данного источника ДИС («дисперсию энтропии»). Мы имеем
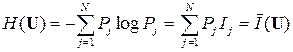 ,
,
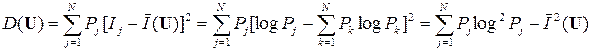 ,
,
или 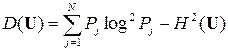 .
.
Однако в математической теории информации величина D(U) не получила полезной интерпретации и соответствующего применения, хотя с её помощью в прикладной теории информации можно приближённо оценивать вероятности поступления в подсистему ПСППС сообщений Si(n), имеющих очень большую информативность I(Si(n)).
Рассмотрим такие источники ДИС {U, P, I, S}, у которых U= {u1, u2}, P= {P1, P2}, то есть бинарные источники ДИС. Для этого введём обозначение: P = P1. При таком обозначении:
P2 = 1 – P, и  (U) ≡ H(U) = H(P) = – P log P – (1 – P) log (1 – P) = H(P) ≡
(U) ≡ H(U) = H(P) = – P log P – (1 – P) log (1 – P) = H(P) ≡ 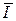 (P).
(P).
Вид функции H(U) ≡  (U) при N = 2 показан на рис. 3. В окрестности точек P = 0 и P = 1 математическая неопределённость функции
(U) при N = 2 показан на рис. 3. В окрестности точек P = 0 и P = 1 математическая неопределённость функции  (P) ≡ H(P) раскрывается по правилу Лопиталя:
(P) ≡ H(P) раскрывается по правилу Лопиталя:
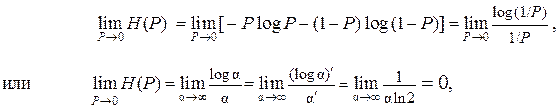
и 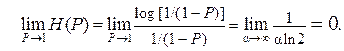 (4.2)
(4.2)
Напротив, при P = 0,5 функция  (P) ≡ H(P) достигает максимума, равного
(P) ≡ H(P) достигает максимума, равного 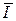 макс ≡ Hмакс = – log (1/2) = 1 (бит/знак). Такой источник дискретной информации ДИС (например – подбрасывание идеальной монеты) может служитьэталономдля измерения удельной информативности (энтропии) любых других источников ДИС, а не только бинарных. Можно создать эталон для десятичной единицы источников дискретных сообщений (например: подбрасывание икосаэдра с дублированным обозначением двадцати его граней цифрами от 0 до 9). Для натуральной единицы – нельзя, так как этот эталон подразумевает источник ДИС с e ≈ 2,718 равновероятными элементарными сообщениями; так что «наты» являются формально-математической конструкцией.
макс ≡ Hмакс = – log (1/2) = 1 (бит/знак). Такой источник дискретной информации ДИС (например – подбрасывание идеальной монеты) может служитьэталономдля измерения удельной информативности (энтропии) любых других источников ДИС, а не только бинарных. Можно создать эталон для десятичной единицы источников дискретных сообщений (например: подбрасывание икосаэдра с дублированным обозначением двадцати его граней цифрами от 0 до 9). Для натуральной единицы – нельзя, так как этот эталон подразумевает источник ДИС с e ≈ 2,718 равновероятными элементарными сообщениями; так что «наты» являются формально-математической конструкцией.
При N > 2 максимальной энтропией Hмакс обладает, как и при N = 2, источник ДИС, у которого все элементарные сообщения (знаки) равновероятны: P1 = P2 = … = PN = P0, где P0 = 1/N.
В этом случае: 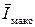 ≡ Hмакс = –
≡ Hмакс = – 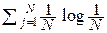 = – log
= – log 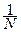 = log N (бит/знак).
= log N (бит/знак).
Это – не что иное, как информационная мера Хартли (см. разд. 1).
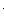
бит 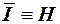
знак




 1
1

 0,5
0,5

0 0,5 1 P
Рис. 3. Зависимость удельной информативности 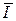 (энтропии H )
(энтропии H )
бинарного источника ДИС от априорной вероятности P знака “единица”
Значит, если у источника ДИСкакой-либо знак uj  U имеет вероятность Pj = 1, то все остальные обязательно имеют нулевую вероятность (это следует из условия
U имеет вероятность Pj = 1, то все остальные обязательно имеют нулевую вероятность (это следует из условия 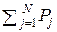 = 1), и H(U) = 0. Если все знаки uj ( j = 1, 2, …, N ) – равновероятны, то
= 1), и H(U) = 0. Если все знаки uj ( j = 1, 2, …, N ) – равновероятны, то  (U) ≡ H(U) = Hмакс = log N. Между этими двумя крайними случаями (Hмин = 0 и Hмакс = log N ) лежат значения удельной информативности (энтропии) всех источников ДИСс алфавитом из N знаков: 0 ≤ {
(U) ≡ H(U) = Hмакс = log N. Между этими двумя крайними случаями (Hмин = 0 и Hмакс = log N ) лежат значения удельной информативности (энтропии) всех источников ДИСс алфавитом из N знаков: 0 ≤ {  ( U ) ≡ H( U )} ≤ log N.
( U ) ≡ H( U )} ≤ log N.
Величина Δ I = log N – H(U) называетсяинформационной избыточностью ДИС, а безразмерная величина
η(U) = Δ I/Hмакс = [log N – H(U)] / log N = 1 – H(U) / log N ≡ 1 –  (U) / log N
(U) / log N
называется коэффициентом избыточности данного источникаДИС; его величина лежит в промежутке [0 ≤ η(U) ≤ 1]. Величина η(U) показывает, в какой мере, при том же количестве знаков N множества U= {uj}  (алфавита U), источник ДИС мог бы производить больше среднего количества информации на один знак, чем это делает данный источник ДИС. Или – то же количество информации можно было бы производить с помощью меньшего количества знаков. Если же «физическая реализация любого знака» uj из совокупности U занимает на носителе запоминающего устройства (на бумаге или в ПЗУ) один и тот же объём памяти (ПЗУ) или же площадь на листе печатного текста, то величина η(U) показывает, во сколько раз меньший объём памяти (или площади листа текста) нужно было бы иметь для хранения данного количества информации, если бы знаки {uj}
(алфавита U), источник ДИС мог бы производить больше среднего количества информации на один знак, чем это делает данный источник ДИС. Или – то же количество информации можно было бы производить с помощью меньшего количества знаков. Если же «физическая реализация любого знака» uj из совокупности U занимает на носителе запоминающего устройства (на бумаге или в ПЗУ) один и тот же объём памяти (ПЗУ) или же площадь на листе печатного текста, то величина η(U) показывает, во сколько раз меньший объём памяти (или площади листа текста) нужно было бы иметь для хранения данного количества информации, если бы знаки {uj}  в различных сообщениях встречались равновероятно (и независимо). Это – первый практический результат наших теоретических построений. Из него следует, что
в различных сообщениях встречались равновероятно (и независимо). Это – первый практический результат наших теоретических построений. Из него следует, что
| перед записью сообщения Si(n) в ОЗУ или ПЗУ его следует «тождественно» (то есть без потери синтактической информации) преобразовать (закодировать) так, чтобы сообщение Si(n) занимало на носителе ОЗУ или ПЗУ минимальный объём памяти. |
Вопросы для самопроверки
1. Как измеряется количество информации, которое содержится в длинных последовательностях элементарных сообщений, выдаваемых источником знаковых (дискретных) сообщений?
2. Что такое удельная информативность (энтропия) источника знаковых (дискретных) сообщений?
3. Каков вид зависимости удельной информативности (энтропии) бинарного источника дискретных сообщений от априорной вероятности одного из элементарных сообщений?
4. Что такое коэффициент избыточности источника дискретных сообщений и в чём состоит его математический и практический смысл?
5. Каково назначение кодера источника дискретных сообщений?
Дата добавления: 2015-05-16; просмотров: 1110;
