Пятый постулат теории информации
Вернёмся к рис. 4. Пусть матрица соответствия Π = || π j k; j, k = 1, 2, …, N || диагонализируема ( | det Π | = 1), так что в отсутствие в канале КПДС помех статическая система передачи информации абсолютно надёжна [ 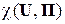 = 1] и потери информации в системе ССПИ не происходит, а между символами {wj}
= 1] и потери информации в системе ССПИ не происходит, а между символами {wj}  и знаками {uj}
и знаками {uj}  имеется одно-однозначное соответствие.
имеется одно-однозначное соответствие.
Из-за наличия в реальных каналах КПДС (в основном – в линиях электросвязи) различного рода естественных и искусственных помех это одно-однозначное соответствие непредсказуемым (случайным) образом нарушается. В простейшем варианте системы ССПИ (см. рис. 5) стохастичность каналаКПДС можно характеризовать квадратной переходной матрицей порядка NП= || Pj k; j, k = 1, 2, …, N ||, элементы которой Pj k = P (wk|uj) есть условные вероятности того, что входному (первичному) знаку uj 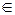 U будет соответствовать (при сканировании произвольного текста) выходной символ wk
U будет соответствовать (при сканировании произвольного текста) выходной символ wk 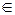 W. При любом значении j = 1, 2, …, N соблюдается равенство
W. При любом значении j = 1, 2, …, N соблюдается равенство 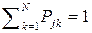 , то есть элементарное сообщение uj в любом случае как-то идентифицируется (решение на выходе декодера: «Не знаю, что за знак был передан по каналу КПДС!» – не принимается). По формуле полной вероятности
, то есть элементарное сообщение uj в любом случае как-то идентифицируется (решение на выходе декодера: «Не знаю, что за знак был передан по каналу КПДС!» – не принимается). По формуле полной вероятности 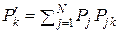 .
.
Понятно, что если переходная матрицаПимеет диагональный вид, то есть П= || δj k; j, k = 1, 2, …, N ||, где δj k = 1 при j = k и δj k = 0 при j ≠ k (δj k – символ Кронекера), то символу wk всегда будет присваиваться значение знака uk – и потерь информации в канале КПДС происходить не будет. Такие системы ССПИ рассматривались в разд. 6.
В общем случае матрицаП– произвольная, с двумя ограничениями:
а) 0 ≤ Pj k ≤ 1;
б ) 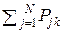 = 1 при любом j = 1, 2, …, N.
= 1 при любом j = 1, 2, …, N.
 помехи
помехи

Π = { Pj k }

 U = {uj}
U = {uj}  P11 P12 … P1 k … P1 N W = {wk}
P11 P12 … P1 k … P1 N W = {wk} 
P = {Pj}  P21 P22 … P2 k … P2 N Pвых = {P'k}
P21 P22 … P2 k … P2 N Pвых = {P'k} 
I = {Ij}  . . . . . . . . . . . . . . . . . . . Iвых ={I'k j; j, k = 1, 2, …, N }
. . . . . . . . . . . . . . . . . . . Iвых ={I'k j; j, k = 1, 2, …, N }
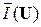 = –
= – 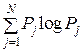 Pj 1 Pj 2 … Pj k … Pj N
Pj 1 Pj 2 … Pj k … Pj N
. . . . . . . . . . . . . . . . . . . .
PN 1 PN 2 … PN k … PN N
Рис. 5. Статическая система передачи
дискретной информации при наличии помех
Отметим также, что величина 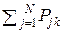 (сумма элементов k-го столбца матрицы П) может лежать в пределах от 0 до N при любом k = 1, …, N, то есть в крайних случаях либо k-му символу wk не будет присвоено ни одного из значений переданных знаков uj
(сумма элементов k-го столбца матрицы П) может лежать в пределах от 0 до N при любом k = 1, …, N, то есть в крайних случаях либо k-му символу wk не будет присвоено ни одного из значений переданных знаков uj 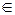 U, либо всем им будет соответствовать выходной символ wk.
U, либо всем им будет соответствовать выходной символ wk.
Каким же образом символу wk 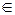 W на выходе КПДС следует присваивать значение некоторого знака uj
W на выходе КПДС следует присваивать значение некоторого знака uj 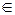 U? Оптимальным решением, с точки зрения математическойстатистики, будет следующее: символу wk нужно присваивать значение uj, апостериорная вероятность которого
U? Оптимальным решением, с точки зрения математическойстатистики, будет следующее: символу wk нужно присваивать значение uj, апостериорная вероятность которого
P(uj|wk) = P(uj) P(wk|uj)/P(wk) = Pj Pjk /P'k
максимальна по всем значениям j = 1, 2, …, N (байесовское решение). В этом случае информационные потери в канале КПДС должны быть минимальными.
Переставим столбцы матрицы П в соответствии с этим правилом принятия решения таким образом, чтобы k-й выходной символ wk соответствовал k-му знаку uk на входеканала КПДС. Тогда знаку uj чаще всего (но не всегда!) будет соответствовать символ wj.
При произвольной матрице П сообщение Si(n) = ( ui1, ui2, …, uik, …, uin ) будет доходить до получателя ПИ в искажённом виде S'i(n) = ( wi1, wi2, …, wik, …, win ), поскольку в общем случае любому символу wik может быть случайным образом присвоено значение любого знака uj. Поэтому возникает вопрос: насколько эти искажения существенны? Поскольку нас интересуют «длинные сообщения» (Si(n), n >> 1), у которых I(Si(n)) ≈ n 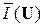 ≡ n H(U), то в простейшем случае, когда помехи в канале КПДС не зависят от знаков uj
≡ n H(U), то в простейшем случае, когда помехи в канале КПДС не зависят от знаков uj 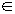 U, нам нужно определить среднюю (на один входной знак uj) потерю синтактической информации при ошибочной идентификации знаков {uj}
U, нам нужно определить среднюю (на один входной знак uj) потерю синтактической информации при ошибочной идентификации знаков {uj}  источника ДИС на выходе канала КПДС.
источника ДИС на выходе канала КПДС.
Казалось бы, количество информации Ij j, которое содержится в выходном символе wj, относительно информации, содержащейся во входном знаке uj – после упорядочения («квазидиагонализации») матрицы П = || Pj k || в соответствии с байесовским правилом идентификации символов wk – можно вычислить по формуле Ij j = Pj j Ij = – Pj j log Pj. Тогда «естественным образом» получается:
при Pj j = 1 величина Ij j = Ij = – log Pj, а при Pj j = 0: Ij j = 0.
Однако это не так, ибо отсутствие в выходном символе wk информации о входном знаке uj соответствует не случаю, когда Pj k = P(wk|uj) = 0, а случаю, когда вероятность Pj k появления на выходе КПДС символа wk не связано статистически с появлением знака uj на его входе, то есть когда
Pj k = P(wk|uj) = P(wk) = P'k, или 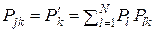 .
.
Поскольку P(uj, wk) = P(uj) P(wk|uj) = P(wk) P(uj|wk), то
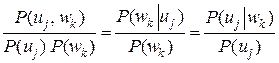 ,
,
и при P(wk|uj) = P(wk), или, что то же самое, при Pjk = P'k справедливо равенство: P(uj|wk) = P(uj).
Если у симметричного бинарного канала КПДС P(wk|uj) = 0,5 = P(wk), то,
как остроумно заметил К. Шеннон ([46], с. 227), линия электросвязи в КПДС вовсе не нужна: получатель информации ПИ может с таким же успехом подбрасывать монету. И хотя половина знаков uj будет идентифицирована на выходе канала КПДС правильно, какие из символов wik в последовательности S'i(n) = (wi1, wi2, …, wik, …, win ) будут соответствовать знакам uj, а какие – нет, получатель информации определить не сможет. В этом случае
P(wk|uj) = P(wk), или Pj k /P'k = 1, или log(Pj k /P'k ) = – log(P'k /Pj k) = 0.
Значит,
величиной Ik j = log(Pj k /P'k) можно характеризовать
количество информации, содержащейся в выходном символе wk 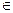 W
относительно входного знака uj W
относительно входного знака uj 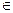 U. U.
|
Если при всех значениях j и k от 1 до N величина Pj k принимает значение либо Pj k = 1, либо Pj k = 0 (то есть Pj k = π j k), то мы приходим к вариантам, рассмотренным нами в разд. 6: Ik j = log(π j k /P'k).
Особенно ясно это видно при анализе потерь информации в бинарных системах передачи сообщений.
Пусть имеется бинарный канал КПДС. Его функционирование можно описать схемой, представленной на рис. 6. Введём следующие обозначения:
P1 = P, P2 = 1 – P, P11 = p, P12 = 1 – p, P22 = q, P21 = 1 – q,
Ik j = log(Pj k /P'k); j, k = 1, 2;
P'1 = P p + (1 – P) (1 – q), P'2 = P (1 – p) + (1 – P) q.
Удельная информативность знаков (энтропия) бинарного источника ДИС
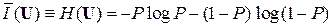 .
.
Рассмотрим случай а) на рис. 6: p = 1, q = 1, p + q = 2. В этом случае потерь информации нет, и среднее количество информации, содержащейся на выходе канала КПДС относительно источника ДИС, определяется из следующих
P11 = p


 (P1 = P ) u1 →¤ ¤→ w1 (P'1)
(P1 = P ) u1 →¤ ¤→ w1 (P'1)
P12 = 1 – p P21 = 1 – q
 (P2 = 1 – P ) u2 →¤ ¤→ w2 (P'2 = 1 – P' )
(P2 = 1 – P ) u2 →¤ ¤→ w2 (P'2 = 1 – P' )
P22 = q
p = 1 p = 0 p = 0



 u1 →¤ ¤→ w1 u1 →¤ ¤→ w1 u1 →¤ ¤→ w1
u1 →¤ ¤→ w1 u1 →¤ ¤→ w1 u1 →¤ ¤→ w1

 u2 →¤ ¤→ w2 u2 →¤ ¤→ w2 u2 →¤ ¤→ w2
u2 →¤ ¤→ w2 u2 →¤ ¤→ w2 u2 →¤ ¤→ w2
q = 1 q = 0 q = 1
а) б ) в)
p = 0,5


 u1 →¤ ¤→ w1
u1 →¤ ¤→ w1
0,5
0,5
 u2 →¤ ¤→ w2
u2 →¤ ¤→ w2
q = 0,5
г)
Рис. 6. Бинарный канал передачи дискретных сообщений
вычислений – в соответствии с формулой (6.2):
P'1 = P; P'2= 1 – P;
P1 P11 I11 = – P log P; P1 P12 I21 = – P·0·log 0 = 0;
P2 P21 I12 = – (1 – P)·0·log 0; P2 P22 I22 = – (1 – P) log (1 – P);
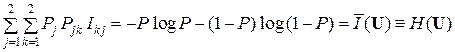 .
.
Вводя обозначение  (U, П) =
(U, П) = 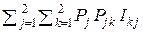 и определяя коэффициент надёжности бинарной системы передачи дискретных сообщений как χ(U, П) =
и определяя коэффициент надёжности бинарной системы передачи дискретных сообщений как χ(U, П) =  (U, П) /
(U, П) /  (U) ≡ χ(P, p, q) в случае а) получим:
(U) ≡ χ(P, p, q) в случае а) получим:
 (U, П) =
(U, П) =  (U), χ(P, 1, 1) = 1.
(U), χ(P, 1, 1) = 1.
Удельная информативность  (U, П) множества символов W на выходе канала КПДС при данном источнике ДИС U на его входе равна:
(U, П) множества символов W на выходе канала КПДС при данном источнике ДИС U на его входе равна:
 (U, П) =
(U, П) = 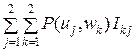 =
= 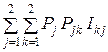 ,
,
или  (U, П) =
(U, П) = 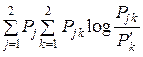 . (7.1)
. (7.1)
Величину R ≡  (U, П) К. Шеннон назвал «скоростью передачи информации» по каналу КПДС ([46], с. 277).
(U, П) К. Шеннон назвал «скоростью передачи информации» по каналу КПДС ([46], с. 277).
Мы будем под величиной  (U, П) подразумевать среднее количество
синтактической информации, передаваемой по каналу КПДС,
на вход которого поступают всевозможные элементарные
сообщения (знаки) uj (U, П) подразумевать среднее количество
синтактической информации, передаваемой по каналу КПДС,
на вход которого поступают всевозможные элементарные
сообщения (знаки) uj 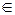 U источника ДИС, а на выходе появляются
символы (вторичные знаки) wk из совокупности W,
приходящейся на один знак из совокупности U(бит/знак),
поскольку рассматриваются статические системы ССПИ U источника ДИС, а на выходе появляются
символы (вторичные знаки) wk из совокупности W,
приходящейся на один знак из совокупности U(бит/знак),
поскольку рассматриваются статические системы ССПИ
|
В варианте а) на рис. 6:
 (U, П) = – P log P – (1 – P ) log (1 – P ) =
(U, П) = – P log P – (1 – P ) log (1 – P ) =  (U) [бит/знак].
(U) [бит/знак].
В общем случае (N ≥ 2) при Pj k = δj k получаем:
Ik j = – δ j k log Pj = – δ j k log (P'k /Pj k) и  (U, П) =
(U, П) =  (U).
(U).
В случае б ) на рис. 6: p = q = 0, p + q = 0. Тогда P11 = P22 = 0, то есть переданному знаку u1 никогда не будет соответствовать выходной символ w1, а знаку u2 – символ w2. Однако это не значит, что информация в такой системе ССПИ будет полностью потеряна. Напротив, если декодер символу w1 будет присваивать значение знака u2, а символу w2 – знака u1 (согласно правилу максимума апостериорной вероятности), то потери информации в канале КПДС вообще не будет происходить и
 (U, П) =
(U, П) = 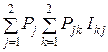 = – (1 – P ) log (1 – P ) – P log P =
= – (1 – P ) log (1 – P ) – P log P =  (U).
(U).
В случае в) на рис. 6: p = 0, q = 1, p + q = 1. Очевидно, что здесь происходит полная потеря информации при любом алгоритме работы декодера, хотя
величина q ≠ 0.
Действительно. Вычислим значение функции  (U, П).
(U, П).
Заметим, что P'1 = 0, а P'2 = 1. Значит:
j = 1, k = 1 ► Pj Pjk = P1 P11 = P · 0 = 0; j = 1, k = 2 ► P1 P11 = P1· 1 = P;
j = 2, k = 1 ► P2 P21 = (1 – P )·0 = 0; j = 2, k = 2 ► P2 P22 = 1 – P;
 (U, П) = 0 – P log 1 + 0 – (1 – P ) log 1 = 0.
(U, П) = 0 – P log 1 + 0 – (1 – P ) log 1 = 0.
Если отнести величину  (U, П) к удельной информативности
(U, П) к удельной информативности  (U) источника ДИС, то в случаях а) ( p + q = 2) и б ) ( p + q = 0) получим: χ(P, p, q) = =
(U) источника ДИС, то в случаях а) ( p + q = 2) и б ) ( p + q = 0) получим: χ(P, p, q) = =  (U, П)/
(U, П)/  (U) = 1, а в случае в): p = 0, q = 1, p + q= 1, χ( P, 0, 1) = 0.
(U) = 1, а в случае в): p = 0, q = 1, p + q= 1, χ( P, 0, 1) = 0.
Величина κ (P, p, q) = 1 – χ (P, p, q) показывает процент потерь информации источника ДИС в канале КПДС; поэтому величину χ (P, p, q) = 1 – κ (P, p, q) следует называтькоэффициентом информационной надёжности статической системы передачи дискретных сообщений (ССПИ ).
В случае г) на рис. 6 ( p = q = 1/2) получаем следующее:
P'1 = 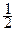 (P + 1 – P) =
(P + 1 – P) = 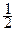 = P'2;
= P'2;
P1 P11 I11 = – P 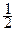 log
log 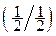 = 0; P1 P12 I21 = 0;
= 0; P1 P12 I21 = 0;
P2 P21 I12 = P2 P22 I22 = 0;  (U, П) = 0; χ(P,
(U, П) = 0; χ(P, 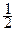 ,
, 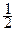 ) = 0,
) = 0,
то есть в этом случае в канале КПДС также происходит полная потеря информации относительно любой достаточно длинной входной последовательности Si(n) = ( ui1, ui2, …, uik, …, uin ), n >> 1.
Рассмотрим общий случай (0 < p < 1, 0 < q < 1) и определим, когда происходит полная потеря информации в системе ССПИ. Теперь уже совершенно ясно, что это произойдёт в случае, если вероятность поступления к получателю ПИ символа wk не зависит от того, какой из знаков uj множества U = {uj} 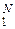 был выдан источником ДИС в канал КПДС, то есть при P (wk|uj) = P (wk).
был выдан источником ДИС в канал КПДС, то есть при P (wk|uj) = P (wk).
При k = 1, j = 1: P(w1) = P'1 = P(w1|u1) = p. 
При k = 1, j = 2: P(w1) = P'1 = P(w1|u2) = 1 – q.
Приравнивая правые части этих равенств, получаем:
p = 1 – q, или p + q = 1, а χ(P, p, q) = 0.
То же самое получается при k = 2. Частные случаи ( p = 0, q = 1: случай в) и p = q = 0,5: случай г) на рис. 6) как раз соответствуют варианту p + q = 1.
Итак,если p + q = 2, то  (U, П) =
(U, П) =  (U), χ(P, p, q) = 1;
(U), χ(P, p, q) = 1;
если p + q = 0, то  (U, П) =
(U, П) =  (U), χ(P, p, q) = 1;
(U), χ(P, p, q) = 1;
если p + q = 1, то  (U, П) = 0, и надёжность канала КПДС становится нулевой: χ(P, p, q) = 0.
(U, П) = 0, и надёжность канала КПДС становится нулевой: χ(P, p, q) = 0.
Значит, мы получили два сечения поверхности χ(P, p, q) по уровням χ = 1 и χ = 0 (см. рис. 7): точки (0, 0, 1) и (1, 1, 1), в которых χ(P, p, q) = 1, и прямую p + q = 1 на плоскости ( p, q), на которой χ(P, p, q) = 0.
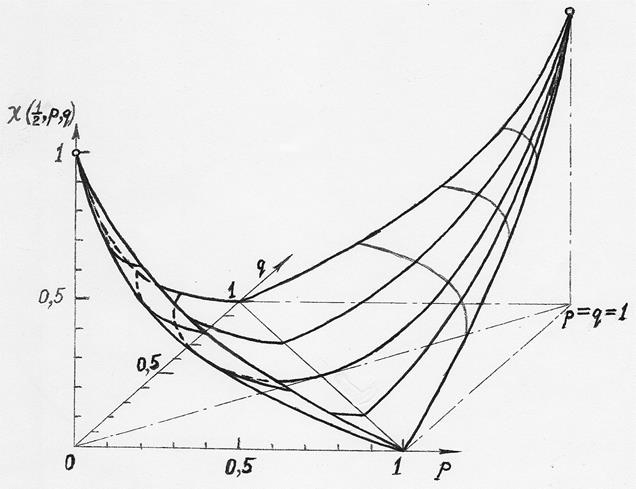
Рис. 7. Зависимость коэффициента информационной надёжности χ
канала КПДС от величин p и q
Если p + q ≠ 2, p + q ≠ 0, а также p + q ≠ 1, то 0 < χ(P, p, q) < 1, и эти две точки и прямую можно соединить, при заданном значении P и различных зна-
чениях p и q, непрерывной поверхностью χ(P, p, q) по формуле:
χ(P, p, q) = 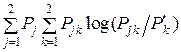 /
/  (U), (7.2)
(U), (7.2)
где P'k = 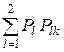 , а
, а  (U) = – P log P – (1 – P) log (1 – P).
(U) = – P log P – (1 – P) log (1 – P).
Зависимость коэффициента надёжности χ(P, p, q) бинарной статической системы передачи семиотической («дискретной») информации ССПИ от переменных p и q при P = 0,5 представлена на рис. 7.
Отметим, что в симметричных бинарных системах ССПИ( p = q) непреднамеренные помехи (естественного и искусственного происхождения) могут снизить величину ( p + q) от значения p + q = 2 ( p = q = 1) до значения p + q = 1 (то есть p = q = 0,5: см. рис. 7). Интервал значений от p + q = 0 ( p = q = 0) до p + q = 1 относится к организованным «противником» помехам в канале КПДС.
Пусть в качестве знаков u1 и символов w1 используется “1”, а в качестве u2 и w2 – “0” (современные бинарные цифровые системы электросвязи). Если «противник» – глупый, то он каждую посланную источником ДИС “единицу” будет ретранслировать как “ноль” и наоборот. Нетрудно распознать такой алгоритм подавления электросвязи и поменять алгоритм работы сканера: “единицам” первичного источника ДИС присваивать значения символов “ноль” и наоборот. В таком случае эффективность противодействия «глупого противника» становится нулевой, а канал передачи информации – стопроцентно надёжным.
Для распознавания субъектами общения такого «глупого противника» им достаточно договориться, что вместе с информационным блоком всегда будет передаваться известная источнику ДИС и получателю ПИ псевдослучайная последовательность, анализ которой и выявит тактику «противника».
В сотовых системах стандарта GSM 900 такая псевдослучайная последовательность служит для оценки текущей надёжности канала КПДС в каждом рабочем кадре (так называемая «обучающая последовательность»).
Максимальная эффективность противодействия обмену информацией между ДИС и ПИ будет иметь место при p + q = 1; например, когда «противник» половину “единиц” будет ретранслировать, по псевдослучайному закону, как “ноли”, а половину “нолей” – как “единицы”.
В этом случае p = q = 0,5 и χ(P, p, q) = 0.
Мы так подробно остановились на вопросе о потере знаковой («дискретной») информации в каналах КПДС при наличии в них непреднамеренных или организованных помех потому, что его решение наиболее трудно для понимания, а в соответствующей литературе по этому вопросу наблюдаются разночтения. В то же время, адекватное решение вопроса о потерях информации в каналах связи и правильная его ( решения) интерпретация имеют фундаментальное значение для понимания прикладной теории информации и её приложений.
Дата добавления: 2015-05-16; просмотров: 815;
