Статических каналов передачи дискретных сообщений. Вернёмся к информационным характеристикам бинарной системы ССПИ (см
Вернёмся к информационным характеристикам бинарной системы ССПИ (см. рис. 6) и рассмотрим теперь зависимость среднего количества информации  (U, П) на один знак дискретного источника сообщений U, передаваемой посредством бинарного канала КПДС с переходной матрицей
(U, П) на один знак дискретного источника сообщений U, передаваемой посредством бинарного канала КПДС с переходной матрицей 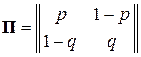 , от характеристик подключаемого к нему источника ДИС, то есть от величины P. В этом случае
, от характеристик подключаемого к нему источника ДИС, то есть от величины P. В этом случае
P'1= P p + (1 – P) (1 – q); P'2 = P (1 – p) + (1 – P) q = 1 – P'1;
и в соответствии с формулой (7.1) имеем
 (U, П) = P [ p log p + (1 – p) log (1 – p)] + (1 – P) [q log q + (1 – q) log (1 – q)] –
(U, П) = P [ p log p + (1 – p) log (1 – p)] + (1 – P) [q log q + (1 – q) log (1 – q)] –
– [P ( p + q – 1) + 1 – q] log [P ( p + q – 1) + 1 – q] –
– [ q – P ( p + q – 1)] log [q – P ( p + q – 1)]. (9.1)
В симметричном бинарном канале ( p = q):
 (U, П) = p log p + (1 – p) log (1 – p) – [P (2p – 1) + 1 – p]×
(U, П) = p log p + (1 – p) log (1 – p) – [P (2p – 1) + 1 – p]×
×log [P (2p – 1) + 1 – p] – [ p – P (2p – 1)] log [ p – P (2p – 1)]. (9.2)
Зависимость величины  (U, П) для симметричного бинарного канала КПДС от величины P представлена кривыми 1 ( p = q = 1) и 2 (0,5 < ( p = q) < 1) на рис. 8.
(U, П) для симметричного бинарного канала КПДС от величины P представлена кривыми 1 ( p = q = 1) и 2 (0,5 < ( p = q) < 1) на рис. 8.
При (0,5 < p < q < 1) зависимость  (U, П) от величины P имеет вид, изображенный кривой 3; при (0,5 < q < p < 1) – кривой 4 на рис. 8.
(U, П) от величины P имеет вид, изображенный кривой 3; при (0,5 < q < p < 1) – кривой 4 на рис. 8.
Величина P = P0, соответствующая максимальному значению  (U, П) =
(U, П) =
=  ( p, q), находится из уравнения d
( p, q), находится из уравнения d  (U, П)/dP = 0. В результате решения этого уравнения получаем:
(U, П)/dP = 0. В результате решения этого уравнения получаем:
P0 = (q – β)/( p + q – 1),
 макс( p, q) = γ (q – β) – β log β – (1 – β) log (1 – β) + q log q + (1 – q) log (1 – q),
макс( p, q) = γ (q – β) – β log β – (1 – β) log (1 – β) + q log q + (1 – q) log (1 – q),
где β = (1 + 2γ) –1, γ = [ p log 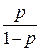 + q log
+ q log 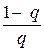 + log
+ log 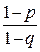 ]/( p + q – 1).
]/( p + q – 1).
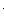
бит 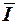
знак




 1
1
1

 0,5
0,5


 ℰ
ℰ
 3
3
 2
2
4

P0 0,5 1 P
Рис. 8. Зависимость среднего на знак количества информации
на выходе бинарного канала КПДС
от вероятности P выдачи знака u1 источником ДИС:
1 – ( p = q = 1); 2 – (0,5 < p = q < 1); 3 – (0,5 < p < q < 1); 4 – (0,5 < q < p < 1)
Естественно, величина  макс( p, q) ≡
макс( p, q) ≡  макс(Π) зависит только от переходныхвероятностей p и q бинарного канала КПДС, а потому может служить егособственной информационной характеристикой – вне зависимости от информационных характеристик подключаемого к нему источника ДИС. Поэтому величину
макс(Π) зависит только от переходныхвероятностей p и q бинарного канала КПДС, а потому может служить егособственной информационной характеристикой – вне зависимости от информационных характеристик подключаемого к нему источника ДИС. Поэтому величину  макс(Π) будем называть удельной информационной ёмкостьюстатического канала КПДС, или просто ёмкостью канала КПДС и обозначать как ℰ (Π) ≡
макс(Π) будем называть удельной информационной ёмкостьюстатического канала КПДС, или просто ёмкостью канала КПДС и обозначать как ℰ (Π) ≡  макс(Π).
макс(Π).
Величина P0 соответствует априорной вероятности одного из первичных знаков бинарного источника ДИС. Этот источник ДИС будет согласован с каналом КПДС, который характеризуется величинами p и q.
Удельная информативность (энтропия) такого согласованного источника ДИС: 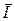 согл ( p, q) ≡ Hсогл ( p, q) ≡ – P0 log P0 – (1 – P0) log (1 – P0), а коэффициент надёжности получившейся оптимальной статической системы передачи бинарной информации ССПИ χ( p, q) =
согл ( p, q) ≡ Hсогл ( p, q) ≡ – P0 log P0 – (1 – P0) log (1 – P0), а коэффициент надёжности получившейся оптимальной статической системы передачи бинарной информации ССПИ χ( p, q) =  макс( p, q)/Hсогл ( p, q).
макс( p, q)/Hсогл ( p, q).
Отсюда практический вывод:
чтобы обеспечить минимум потерь информации в бинарном канале
КПДС с переходными вероятностями (0,5 < p < 1) и (0,5 < q < 1),
нужно так перекодировать, с помощью промежуточных символов 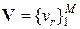 , первичный источник ДИС, чтобы вероятность P выдачи
кодового слова для знака u1 соответствовала величине P0. , первичный источник ДИС, чтобы вероятность P выдачи
кодового слова для знака u1 соответствовала величине P0.
|
Что же происходит при 0 < p < 0,5 и 0 < q < 0,5?
Рассмотрим симметричный бинарный канал КПДС с симметричным бинарным источником ДИС: P = 0,5; p = q. В этом случае, в соответствии с формулой (7.1), величина Ik j = log (Pj k /P'k), и мы имеем:
P'1 = P'2 = 0,5; I11 = log (2 p); I21 = log [2 (1 – p)];
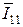 = 0,5 p log (2 p);
= 0,5 p log (2 p); 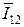 = 0,5 (1 – p) log [2(1 – p)].
= 0,5 (1 – p) log [2(1 – p)].
Графики зависимости величин I11, I21, 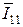 и
и 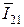 от значения величины p представлены на рис. 9.
от значения величины p представлены на рис. 9.
Из рис. 9 следует, что при p = 0,5 количество информации I11 в символе w1 относительно знака u1 равно нулю (I11 = 0), а при p < 0,5 – становится отрицательным, что не отвечает интуитивному пониманию термина «информация». Зато при p < 0,5 величина I12 становится положительной. Это значит, что при 0,5 < p < 1 символу w1 следует присваивать значение знака u1, а при 0 < p < 0,5 – значение u2. При этом сумма среднего количества информации 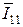 +
+ 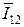 , содержащейся в символе w2, всегда будет величиной неотрицательной при любом значении p.
, содержащейся в символе w2, всегда будет величиной неотрицательной при любом значении p.
Следовательно, рассчитанное по формуле (7.1) количество выходной ин-
формации 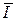 всегда будет положительной величиной, за исключением случая p = 0,5, когда происходит полная потеря информации: I11 = I12 = I21 = I22 = 0.
всегда будет положительной величиной, за исключением случая p = 0,5, когда происходит полная потеря информации: I11 = I12 = I21 = I22 = 0.
| Именно при таком (байесовском) алгоритме работы системы ССПИ реализуются формально-теоретические оценки, даваемые прикладной теорией информации. |
В рассматриваемой системе ССПИ (P = 0,5; p = q) среднее количество информации, получаемое на выходе бинарного канала КПДС,  (U, П) ≡ ≡ H(U, П) (бит/знак), численно равна его коэффициенту надёжности χ(½, p, q) и составляет
(U, П) ≡ ≡ H(U, П) (бит/знак), численно равна его коэффициенту надёжности χ(½, p, q) и составляет
 (U, П) = 1 + p log p + (1 – p) log (1 – p) = χ( p). (9.3)
(U, П) = 1 + p log p + (1 – p) log (1 – p) = χ( p). (9.3)
 бит Ikj
бит Ikj
знак




 1
1


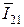 I21 I11
I21 I11 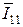



 0
0
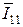
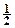
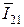 1 p
1 p
 – 1
– 1
I11 I21
 – 2
– 2
Рис. 9. Зависимость информационных характеристик I k j
симметричного бинарного канала КПДС
от значений его переходных вероятностей p = q
В общем случае (при N > 2) решением системы N 2 уравнений относительно величин Pjk можно вычислить те значения Pjk(0), которые определяют переход величин Ik j через “ноль” – и соответствующим образом сконструировать (сравнением данных значений {Pjk} с граничными {Pjk(0)} 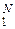 ) алгоритм присвоения символам {wk}
) алгоритм присвоения символам {wk} 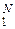 соответствующих значений знаков {uj}
соответствующих значений знаков {uj} 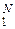 . По существу именно таким образом реализуется байесовский критерий принятия решений.
. По существу именно таким образом реализуется байесовский критерий принятия решений.
В то же время, можно сформулировать следующее утверждение.
Если удельная информативность 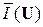 , или энтропия H(U)
данного источника ДИС не более
удельной информационной ёмкости ℰ (П) статического канала
передачи КПДС, имеющего переходную матрицу П,
то можно так закодировать знаки {uj} , или энтропия H(U)
данного источника ДИС не более
удельной информационной ёмкости ℰ (П) статического канала
передачи КПДС, имеющего переходную матрицу П,
то можно так закодировать знаки {uj} 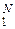 источника ДИС U,
что передача длинных сообщений Si(n) (n >> 1) источника ДИС
посредством статического канала КПДС будет почти безошибочной.
Если ℰ (П) < H(U), то не существует способа кодирования знаков {uj} источника ДИС U,
что передача длинных сообщений Si(n) (n >> 1) источника ДИС
посредством статического канала КПДС будет почти безошибочной.
Если ℰ (П) < H(U), то не существует способа кодирования знаков {uj} 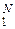 ,
который бы позволил передавать информацию с коэффициентом
информационной надёжности бóльшим, чем χ(U, П) = ℰ (П)/H(U).
Иначе: при H(U) ≥ ℰ (П) средняя потеря информации на один знак
источника ДИС будет не меньше, чем разность Δ(U, Π) = H(U) – ℰ (П). ,
который бы позволил передавать информацию с коэффициентом
информационной надёжности бóльшим, чем χ(U, П) = ℰ (П)/H(U).
Иначе: при H(U) ≥ ℰ (П) средняя потеря информации на один знак
источника ДИС будет не меньше, чем разность Δ(U, Π) = H(U) – ℰ (П).
|
Получив в разд. 9 достаточно существенные для практических приложений общетеоретические результаты теории информации, перейдём к способам их практической реализации.
Вопросы для самопроверки
1. Каким образом вычисляется удельная информативность бинарной системы передачи дискретных сообщений?
2. Что такое информационная ёмкость бинарного канала передачи дискретных сообщений и в чём состоит её практический смысл?
3. Каким образом вычисляется коэффициент информационной надёжности симметричного бинарного канала передачи дискретных сообщений?
4. Каким образом соотносятся между собой удельная информативность источника дискретных сообщений и информационная ёмкость статического канала передачи дискретных сообщений?
Дата добавления: 2015-05-16; просмотров: 928;
