Совместная, условная и остаточная энтропии каналов электросвязи
В разд. 7 мы подробно обсудили общетеоретическую проблему оценивания количества информации, получаемой на выходе канала статической системы передачи информации (ССПИ) относительно поступающей на её вход информации от источника ДИС, при наличии в канале КПДС непреднамеренных и (или) организованных помех. Мы ввели в рассмотрение пятый постулат
(Шеннона) теории информации:
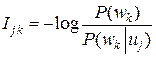
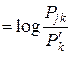 , (8.1)
, (8.1)
где Ik j – количество информации, содержащейся в символе wk относительно переданного знака uj; P(wk|uj) ≡ Pjk – jk-й элемент переходной матрицы П канала КПДС; P(wk) ≡ P'k – полная вероятность появления на выходе системы ССПИ символа wk: P(wk) ≡ P'k 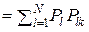 .
.
Среднее (на один знак) количество информации на выходе канала КПДС  (U, П) будем называть удельной информативностью статической системы ССПИ и вычислять по формуле [см. определение (7.4)]:
(U, П) будем называть удельной информативностью статической системы ССПИ и вычислять по формуле [см. определение (7.4)]:
 (U, П) =
(U, П) = 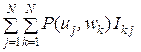 =
= 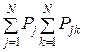 log
log 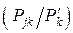 . (8.2)
. (8.2)
Формулу (8.2) будем называть естественной формой записи для удельной информативности  (U, П) системы ССПИ, поскольку эта формула выражает величину
(U, П) системы ССПИ, поскольку эта формула выражает величину  (U, П) через априорные вероятности Pj элементарных сообщений uj источника ДИС U и элементы Pj k переходной матрицы П канала КПДС.
(U, П) через априорные вероятности Pj элементарных сообщений uj источника ДИС U и элементы Pj k переходной матрицы П канала КПДС.
Формы записи (8.1) и (8.2) имеют следующее практическое значение. Каналы КПДС можно – статистически – исследовать отдельноот возможных источников ДИС, которые будут подключаться к каналу КПДС (оценивать величины {Pjk} 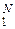 ). Различные источникиДИС исследуются отдельно: оцениваются величины {Pj}
). Различные источникиДИС исследуются отдельно: оцениваются величины {Pj} 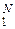 . Затем (уже теоретически!) можно, с помощью перекодирования сообщений источника ДИС, согласовать источник ДИС и канал КПДС так, чтобы реализовать его максимальную информационную надёжность с коэффициентом надёжности χ(П).
. Затем (уже теоретически!) можно, с помощью перекодирования сообщений источника ДИС, согласовать источник ДИС и канал КПДС так, чтобы реализовать его максимальную информационную надёжность с коэффициентом надёжности χ(П).
Это позволяет приступить к определению информационных характеристик системы ССПИ и к решению Центральной проблемы №5 ПТИ: оценивание предельно достижимой информационной надёжности систем ССПИ с использованием формул (8.2) и (7.5). Однако перед этим рассмотрим другие возможные формы записи выражения (8.2).
Симметричная форма записи (Шеннон, 1948 г.: [46], разд. 6; Вудворд, 1953 г.: [12], гл. II).
Запишем выражение (8.1) в виде: Ik j = log [P(wk | uj) /P(wk)].
Умножим числитель и знаменатель дроби в этом выражении на Pj = P (uj):
Ik j = log {P(uj) ·P(wk | uj) /[P(uj) ·P(wk)]} = log {Pj ·Pj k /(Pj ·P'k)}.
Но P(uj)P(wk|uj) = Pj ·Pj k = P(uj, wk). Значит, Ik j = log {P(uj, wk) /[P(uj)P(wk)]},
а 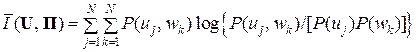 , (8.3)
, (8.3)
или  (U, П) =
(U, П) = 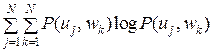 –
–
– 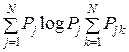 –
– 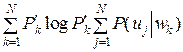 .
.
Так как знак uj 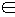 U в какой-нибудь из символов wk
U в какой-нибудь из символов wk 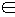 W переходит, а при приёме символа wk
W переходит, а при приёме символа wk 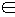 W какой-нибудь из знаков uj
W какой-нибудь из знаков uj 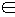 U был передан, то
U был передан, то
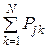 =
= 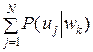 = 1.
= 1.
Отсюда получаем:
 (U, П) = H(U) + H(W) – H(U, W), (8.4)
(U, П) = H(U) + H(W) – H(U, W), (8.4)
где H(U) – энтропия источника ДИС, интерпретируемая как его удельная информативность  (U);
(U);
H(W) – формальная энтропия совокупности символов {wk} 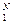 на выходе канала КПДС: H(W) =
на выходе канала КПДС: H(W) = 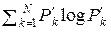 ;
;
H(U, W) – совместная энтропия совокупности символов {uj} 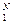 и {wk}
и {wk} 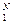 на входе и выходе канала КПДС: H(U, W) =
на входе и выходе канала КПДС: H(U, W) = 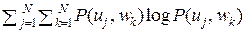 .
.
Запись (8.3) имеет симметричный относительно знака uj и символа wk вид. На этом основании нельзя делать вывод о том, что
| «количество информации, содержащейся в символе wkотносительно знака uj, такое же, как и в знаке uj относительно символа wk». |
Ведь субъект-ДИС может ничего не знать о том, что произошло в канале КПДС с посланным им элементарным сообщением (знаком) uj! Например – при радиовещании.
Поэтому этот формально-теоретический вывод имеет такую же силу, как вывод о «возможности обратить время вспять», делаемый на основании симметрии относительно параметра «время» соответствующих уравнений классической механики. Тем не менее, симметричная форма (8.3) имеет большое практическое значение.
Пусть источник ДИС неразрывно связан с каналомКПДС. Тогда, набрав экспериментально достаточно большую выборку из пар {(ui1, wi1), (ui2, wi2), …, (uin, win)} и оценив статистически вероятности P(uj, wk), можно определить величины P(uj) = 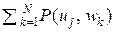 , P(wk) =
, P(wk) = 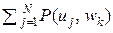 , вычислить все значения Ik j ( j, k = 1, 2, …, N ) и построить оптимальный (байесовский) алгоритм присвоения символам wk значений элементарных сообщений (знаков) uj для данной, не разделяемой на источник ДИС и канал КПДС, статической системы передачи семиотической информации.
, вычислить все значения Ik j ( j, k = 1, 2, …, N ) и построить оптимальный (байесовский) алгоритм присвоения символам wk значений элементарных сообщений (знаков) uj для данной, не разделяемой на источник ДИС и канал КПДС, статической системы передачи семиотической информации.
Негэнтропийная форма записи (К. Шеннон, 1948 г.: [46], разд. 12).
Поскольку P(uj, wk) = P(uj) P(wk|uj) = P(wk) P(uj|wk), то P(wk|uj) /P(wk) = = P(uj|wk) /P(uj).
Поэтому в выражении Ik j = log (Pj k /P'k) можно заменить дробь Pjk /P'k на дробь P(uj|wk) /P(uj) и получить:
Ik j = log [P(uj|wk) /P(uj)] = – log Pj – [– log P(uj|wk)]. (8.5)
Усреднив выражение (8.5) для Ik j по ансамблям U и W, получим:
 (U, П) = H(U) –
(U, П) = H(U) – 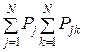 log [1/P(uj|wk)],
log [1/P(uj|wk)],
или H(U, W) = H(U) – H(U|W), (8.6)
где H(U|W) = – 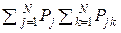 log P(uj|wk). Величину H(U|W) К. Шеннон, по аналогии с остаточной дисперсией в регрессионном анализе математической статистики, назвал «остаточной неопределённостью» (equivocation), то есть энтропией на выходе каналаКПДС. (В [46], с. 277, термин “equivocation” не совсем точно переведён как «ненадёжность».)
log P(uj|wk). Величину H(U|W) К. Шеннон, по аналогии с остаточной дисперсией в регрессионном анализе математической статистики, назвал «остаточной неопределённостью» (equivocation), то есть энтропией на выходе каналаКПДС. (В [46], с. 277, термин “equivocation” не совсем точно переведён как «ненадёжность».)
Математический смысл величины H(U|W) – условная энтропия (неопределённость) знаков uj из ансамбля U при условии, что на выходе канала КПДС приняты всевозможные символы wk из ансамбля W.
Если в формулу (8.6) подставить легко оцениваемые эмпирически или определяемые теоретически величины {Pj} 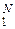 и {Pjk}
и {Pjk} 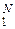 , то получаетсяисходное (постулируемое) выражение (7.4) для
, то получаетсяисходное (постулируемое) выражение (7.4) для  (U, П).
(U, П).
Выражение (8.6) многие авторы, следуя К. Шеннону, интерпретируют следующим образом. Если в канале КПДСотсутствуют помехи и матрица соответствия П – диагонализируемая [коэффициент надёжности χ(П) = 1], то потери информации в канале КПДС не происходит, и до приёма субъектом-ПИ некоторого элементарного сообщения (знака) uj неопределённость получения им одного из знаков uj 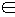 U в среднем равна H(U). После приёманекоторого знака uj
U в среднем равна H(U). После приёманекоторого знака uj 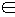 U субъект-ПИ получил количество синтактической информации, равное Ij = – log Pj, а неопределённость ситуации оказалась «снятой». Если же в канале КПДС имеются помехи (0 ≤ χ(П) < 1), то при получении символа wk остаётся неопределённость (equivocation, буквально – уклончивость от прямого ответа) относительно того, какой из знаков uj
U субъект-ПИ получил количество синтактической информации, равное Ij = – log Pj, а неопределённость ситуации оказалась «снятой». Если же в канале КПДС имеются помехи (0 ≤ χ(П) < 1), то при получении символа wk остаётся неопределённость (equivocation, буквально – уклончивость от прямого ответа) относительно того, какой из знаков uj 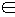 U был передан источником ДИС на самом деле. Поэтому среднее количество информации, получаемое на выходе канала КПДС на один знак источника ДИС, равно:
U был передан источником ДИС на самом деле. Поэтому среднее количество информации, получаемое на выходе канала КПДС на один знак источника ДИС, равно:  (U, П) = H(U) – H(U|W), – а величину H(U|W), по аналогии с условной вероятностью P(uj|wk), называют условной энтропией входа канала КПДС. Это – энтропия (остаточная неопределённость) источника ДИС U при условии получения на выходе канала КПДС всевозможных символов wk
(U, П) = H(U) – H(U|W), – а величину H(U|W), по аналогии с условной вероятностью P(uj|wk), называют условной энтропией входа канала КПДС. Это – энтропия (остаточная неопределённость) источника ДИС U при условии получения на выходе канала КПДС всевозможных символов wk 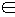 W. При этом остаточную неопределённость H(U|W) ещё нужно реализовать – разработкой соответствующего (байесовского) алгоритма присвоения символам {wk}
W. При этом остаточную неопределённость H(U|W) ещё нужно реализовать – разработкой соответствующего (байесовского) алгоритма присвоения символам {wk} 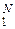 значений знаков {uj}
значений знаков {uj} 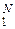 согласно принципу максимума апостериорной вероятности P(uj|wk)! Тем не менее, говорят, что (вообще):
согласно принципу максимума апостериорной вероятности P(uj|wk)! Тем не менее, говорят, что (вообще):
| информация, получаемая субъектом-ПИ с помощью канала КПДС (при наличии в нём помех), есть снятая неопределённость, илинегэнтропия. |
Такая интерпретация аналогична законам сохранения в теоретической физике и не требует тщательного анализа структуры конкретнойинформационной эрготехнической системы и её функционирования– и разработки соответствующих оптимальных алгоритмов её работы. К сожалению, негэнтропийная интерпретация формулы (8.6) породила многочисленные спекуляции на тему «информация и энтропия», несмотря на то, что К. Шеннон предупреждал об опасности такого «обобщения» в заметке «Бандвагон» (см. Введение), а его коллега Дж. Пирс отмечал бессодержательность этой темы (см. разд. 4).
Эти недоразумения порождены интерпретацией сущности обмена сообщениями субъектов информационного взаимодействия как выбора из множества априори известных сообщений некоторого произвольного сообщения и передача этого сообщения по каналу КПДС при наличии в нём различного рода помех (см. Прил.1).
Пятый постулат (8.1) и его следствие (8.2), видимо, – самое выдающееся достижение Клода Шеннонав математической теории информации.
Вопросы для самопроверки
1. Что такое удельная информативность статической системы передачи информации?
2. Что такое естественная форма записи удельной информативности системы передачи информации и почему она так называется?
3. В чём состоит практическое значение естественной формы записи удельной информативности системы передачи информации?
4. Что такое симметричная форма записи удельной информативности системы передачи информации и в чём состоит её математический смысл?
5. Что называется совместной и условной энтропией статической системы передачи информации?
6. Каково практическое значение симметричной формы записи удельной информативности системы передачи информации?
7. Что такое негэнтропийная форма записи удельной информативности системы передачи информации и в чём состоит её математический смысл?
8. Что называется остаточной энтропией статической системы передачи информации и в чём состоит её математический смысл?
9. Каково практическое значение негэнтропийной формы записи удельной информативности системы передачи информации?
Дата добавления: 2015-05-16; просмотров: 1170;
