Основные термины теории блочного кодирования.
Длина избыточных кодовых блоков . . . . . . . . . . . . . . . . . . . . . . . . . . . . . n.
Основание кода . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . M.
Число разрешённых кодовых комбинаций (мощность кода) . . . . . . . . . N.
Полное число кодовых комбинаций (блоков) . . . . . . . . . . . . . . . . . . . . . N0.
Число информационных символов в блоке (кодовом слове) . . . . . . . . . m.
Число проверочных символов в кодовых блоках . . . . . . . . . . . . k = n – m.
Число единиц в кодовых блоках (вес кодового слова) . . . . . . . . . . . . . . P.
Коэффициент избыточности кода . . . . . . . . . . . . . . . . . . . . . . . kпк = 1 – m/n.
Число разрядов (двоичных позиций), в которых кодовая комбинация Bi
отличается от кодовой комбинации Bj ( расстояние Хэмминга) . . d(Bi, Bj).
Для двоичного кода d(Bi, Bj) = 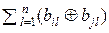 .
.
| Кодовым расстояниемdдля данного кода называется наименьшая из величин {d(Bi, Bj); i, j = 1, 2, …, n}. |
Хэмминг в 1947 г. (соответствующая статья была опубликована лишь в 1950 г.) доказал, что
| если d = 2, то данный код обнаруживает любую однократную ошибку. Для обнаружения всех ошибок кратности r требуется избыточный код с величиной d ≥ (r + 1). Для исправления кодовых ошибок кратности r нужно иметь код с кодовым расстоянием d ≥ (2 r + 1). |
Если основание кода M = 2, то линейные блочные коды называются групповыми, поскольку всевозможные кодовые комбинации такого кода образуют математическую структуру, называемую группой. В любой группе определена одна математическая операция, обозначаемая как ⊗ (аналогично умножению).
Математическая группа G обладает следующими четырьмя свойствами.
1. Замкнутостью: если a 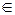 G и b
G и b 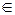 G, то элемент c = a⊗b также принадле-
G, то элемент c = a⊗b также принадле-
жит G: c 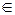 G.
G.
2. Для операции ⊗ справедлив ассоциативный закон:
a⊗(b⊗c) = (a⊗b)⊗c.
3. Группа G содержит единицу: e⊗a = aи a⊗e = a.
4. Для каждого элемента a 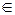 G существует обратный элемент a –1 такой, что a –1⊗ a = e и a⊗a –1 = e.
G существует обратный элемент a –1 такой, что a –1⊗ a = e и a⊗a –1 = e.
Если a 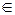 G, b
G, b 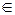 G и a⊗b = b⊗a, то есть все элементы группы перестановочны, то такая группа называется коммутативной, или абелевой (по имени норвежского математика Нильса Абеля: 1802-1829). Операцию ⊗, определяющую группу G, называют (абстрактным) умножением.
G и a⊗b = b⊗a, то есть все элементы группы перестановочны, то такая группа называется коммутативной, или абелевой (по имени норвежского математика Нильса Абеля: 1802-1829). Операцию ⊗, определяющую группу G, называют (абстрактным) умножением.
В качестве абстрактного умножения мы будем использовать алгебраическое умножение матриц и векторов со сложением по модулю два.
Например, 
В групповых кодах элементами группы G являются всевозможные информационные блоки {wj}  , записываемые как векторы-столбцы размера m ×1:
, записываемые как векторы-столбцы размера m ×1:
 , а разрешённые кодовые комбинации избыточного кода
, а разрешённые кодовые комбинации избыточного кода 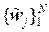 как векторы
как векторы  размера n ×1:
размера n ×1:  = || wj1, wj2, …, wj m, wj, m+1, …, wj n || т.
= || wj1, wj2, …, wj m, wj, m+1, …, wj n || т.
Тогда
| любой линейный код (n, m) можно получить из m линейно независимых кодовых комбинаций путём их посимвольного суммирования по модулю 2. Исходные комбинации называются базиснымии образуют базис кода. |
Матрица 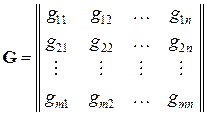 размера m×n называется матрицей,
размера m×n называется матрицей,
порождающей (производящей) данный избыточный код. Процедура кодирования в таком случае эквивалентна алгебраической операции 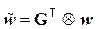 . Матрица G должна храниться в постоянном запоминающем устройстве (ПЗУ) кодера канала КПДС.
. Матрица G должна храниться в постоянном запоминающем устройстве (ПЗУ) кодера канала КПДС.
Если матрицы G1 и G2 отличаются только расположением столбцов, то они порождают эквивалентные коды. Поэтому естественным базисомкода является единичная матрица порядка m: E(m) = || δ jk; j, k = 1, 2, …, m ||, где δ jk – символ Кронекера. Естественная порождающая матрица G имеет вид:

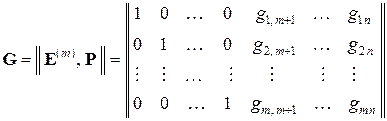 m строк
m строк
m столбцо 
 в k = n – m столбцов
в k = n – m столбцов
Здесь E(m) – единичная матрица порядка m, а P – подматрица проверочных (контрольных) символов размера m×(n – m) = m×k.
Построим проверочную матрицу H размера k×n в виде столбца проверочных векторов:



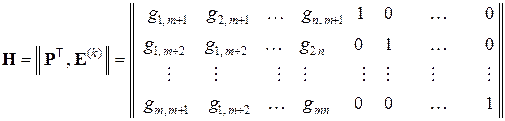 k строк
k строк
m столбцов k = n – m столбцов
Если вектор 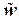 принадлежит к разрешённым кодовым комбинациям, то
принадлежит к разрешённым кодовым комбинациям, то
должны выполняться тождества hi ⊗ 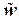 = 0; i = 1, 2, …, k; hi – i-я строка матрицы H.
= 0; i = 1, 2, …, k; hi – i-я строка матрицы H.
Отсюда следует, что H GТ = 0. Здесь: 0 – нулевая матрица размера k × m:


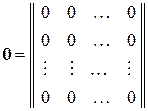 . k строк
. k строк
m столбцов
Значит, для нахождения проверочной матрицы H имеется уравнение:
H⊗GТ  .
.
Однако при k > 2, согласно теореме Хэмминга, мы не только можем обнаруживать r = (k – 1)/2-кратные ошибки, но и исправлять некоторые из них или даже все. Для этого мы должны построить корректирующий (исправляющий) вектор, или вектор-синдром c.
При наличии в принятом векторе (кодовом слове) 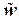 имеются ошибки, то при некоторых значениях i (i = 1, 2, …, k) равенство hi ⊗
имеются ошибки, то при некоторых значениях i (i = 1, 2, …, k) равенство hi ⊗ 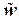 = 0 соблюдаться не будет, а значит в соответствующем разряде l (hl ⊗
= 0 соблюдаться не будет, а значит в соответствующем разряде l (hl ⊗ 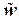 ≠ 0) присутствует ошибка, и заменой “единицы” на “ноль” или “ноля” на “единицу” мы эту ошибку можем исправить. Корректирующий вектор c будет иметь вид c = H ⊗
≠ 0) присутствует ошибка, и заменой “единицы” на “ноль” или “ноля” на “единицу” мы эту ошибку можем исправить. Корректирующий вектор c будет иметь вид c = H ⊗ 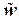 .
.
Познакомимся также с циклическими линейными блочными кодами.
Циклический код обладает свойством цикличности, то есть каждая циклическая перестановка кодовой комбинации также является кодовой комбинацией этого же кода. Кодовые комбинации a циклических кодов образуют циклическую группу G* [20]. Циклическая группа G* состоит из степеней одного элемента a (a0 = e, a, a2, …) и обязательно коммутативна. Каждый элемент a из абелевой группы G порождает в группе G циклическую подгруппу Ga*, состоящую из всех степеней вектора a. Порядок l этой подгруппы Ga* равняется такому наименьшему натуральному числу l, при котором a l = e, то есть минимальному числу циклов l, при котором вектор a l возвращается к единичному вектору e.
Аналогичными свойствами обладают обычные полиномы. Поэтому циклические коды лучше всего задавать не порождающими матрицами G, а порождающими полиномами g(x).
Рассмотрим группу полиномов Gn* одной и той же степени n и их свойства. Возьмём произвольный полином g(x) степени n ≥ 1:
g(x) = g0 + g1 x + g2 x 2 + … + gn x n.
Умножим полином g(x) на аргумент x; получим:
x g(x) = g0 x+ g1 x 2+ g2 x 3 + … + gn x n + 1.
Введём абстрактное умножение ⊗ по правилу: x⊗g(x) = x g(x) [mod (x n – 1)], то есть x⊗g(x) = gn + g0 x+ g1 x 2+ g2 x 3 + … + gn-1 x n. Обозначение mod (x n – 1) означает, что если l > n, то x l = x l – n x n = x l – n, то есть x n = 1 = x0.
Если же к обеим частям равенства x n = 1 прибавить единицу (по модулю два), то получим: x n + 1 = 0.
Полином g1(x) = x⊗g(x) будет иметь степень n так же, как и g(x), то есть будет принадлежать группе Gn*, поскольку он получен циклической перестановкой коэффициентов ( g0, g1, g2, …, gn –1, gn) со «сдвигом этих коэффициентов вправо».
В теории циклических кодов принято представлять кодовые слова в виде полиномов: 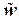 (x) = g0 + g1 x + g2 x 2 + … + gn – 1 x n – 1, то есть количество членов полинома, соответствующему кодовому блоку
(x) = g0 + g1 x + g2 x 2 + … + gn – 1 x n – 1, то есть количество членов полинома, соответствующему кодовому блоку 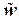 , есть n, а его степень: n – 1.
, есть n, а его степень: n – 1.
Если b – кодовый блок, получающийся из блока a циклическим сдвигом на один разряд влево, то соответствующий ему полином b(x) получается из предыдущего a(x) умножением последнего на x: b(x) = x a(x) [mod (x n – 1)], пользуясь тем, что x n ≡ 1 [mod (x n – 1)].
Сдвиги вправо или влево на j разрядов дают соответственно полиномы
bj(x) = x j⊗a(x) [mod (x n – 1)] и b– j(x)⊗x j = a(x) [mod (x n – 1)].
Если p(x) – произвольный полином, а c(x) – кодовый блок циклического (n, m) кода, то p(x)⊗c(x) [mod (x n – 1)] – тоже кодовый блок этого кода.
Порождающим полиномом циклического (n, m) кода C называется такой ненулевой полином 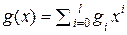 , степень которого наименьшая с коэффициентом при старшей степени gl, равным единице.
, степень которого наименьшая с коэффициентом при старшей степени gl, равным единице.
«Чистые математики» доказали:
а) если C – циклический (n, m) код и g(x) – порождающий его полином, то степень g(x) равна k = n − m и каждый кодовый полином c(x) может быть единственным образом представлен в виде c(x) = xr⊗g(x), где степень r меньше или равна числу (m − 1);
б ) порождающий полином g(x) циклического (n, m) кода является делителем бинома (x n – 1) или же (x n + 1).
Отсюда следует, что в качестве порождающего полинома можно выбирать любой полином, который является делителем бином (1 + x n). Степень n выбранного полинома будет определять количество проверочных символов k и число информационных символов m = n − k. Действительно. При абстрактном умножении полинома g(x) степени k на x m мы должны возвратиться к изначальному полиному g(x) степени k. Чтобы это произошло, необходимо и достаточно, чтобы выполнялось равенство n = m + k, то есть чтобы «модульный полином» (x n + 1) делился на полином g(x) без остатка.
Свяжем порождающий полином g(x) циклического кода C с соответствующей этому коду порождающей (производящей) матрицей G.
Полиномы g(x), x⊗g(x), x 2⊗g(x), …, x k–1⊗g(x) линейно независимы; иначе выполнялось бы тождество: x r⊗g(x) = 0 при любом ненулевом r, что невозможно. Поэтому производящая матрица G имеет в качестве строк векторы, соответ-
ствующие полиномам g(x), x⊗g(x), x 2⊗g(x), …, x m–1⊗g(x).
Матрицу G можно записать в символьной форме (то есть с помощью символов g = 1 или g = 0) в виде:
 .
.
Для каждого кодового блока c циклического кода C справедливо:
c(x)⊗g(x) = 0 [mod g(x)]. Поэтому проверочную матрицу можно записать в виде:
H = || 1 x x2 … xn –2 xn –1 || [mod g(x)].
Тогда: c ⊗HT =  [mod g(x)].
[mod g(x)].
Рассмотрим конкретный пример циклического кода (7, 4) *).
В качестве делителя (x 7 − 1) выбираем порождающий полином третьей степени g(x) = 1+ x + x3. Действительно:
 x 7 + 1 │x3 + x + 1
x 7 + 1 │x3 + x + 1
x7 + x5 + x4 x4 – x2 – x + 1
– x5 – x4
– x5 – x3 – x2
– x4 + x3 + x2
– x4 – x2 – x
x3 + x + 1
x3 + x + 1
0.
____________________________________________________________________
*)Пример заимствован у А. А. Харкевича: Борьба с помехами. – М.: Наука, 1965. – С. 224.
Тогда полученный код будет иметь длину n = 7, число проверочных символов (степень порождающего полинома) k = 3, число информационных символов m = 4, минимальное расстояние d = 3.
Порождающая матрица кода есть:
 , что соответствует вектору
, что соответствует вектору 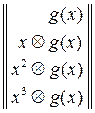 .
.
В матрице G первая строка представляет собой запись полинома g(x) по возрастающим степеням с дополнением строки нулевыми элементами до конца строки, чтобы получилось у матрицы G семь (n = 7) столбцов.
Остальные строки матрицы G – циклические сдвиги первой строки.
Проверочная матрица кода (7, 4):
 ,
,
где i-й столбец, начиная с нулевого, представляет собой остаток от деления x i на полином g(x), записанный по возрастанию степеней, начиная сверху.
Так, например, четвёртый столбец получается следующим образом:
h4(x) = x 3 [mod {g(x) = x + 1}], или в векторной записи: || 110 ||.
Легко убедиться, что G⊗HT = 0.
Существуют также итеративные и каскадные блочные коды.
Теперь уже можно рассмотреть непрерывные свёрточные коды.
При свёрточном кодировании преобразование информационных последовательностей Si(n) в выходные кодовые происходит непрерывно. Кодер двоичного свёрточного кода содержит сдвигающий регистр из m разрядов и сумматоры «по модулю два» для образования кодовых символов 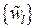 в выходной последовательности. Входы сумматоров соединены с определёнными разрядами регистра. Коммутатор на выходе устанавливает очерёдность посылки кодовых символов в канал связи.
в выходной последовательности. Входы сумматоров соединены с определёнными разрядами регистра. Коммутатор на выходе устанавливает очерёдность посылки кодовых символов в канал связи.
Структуру кода определяют следующие характеристики.
1. Число информационных символов 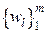 , поступающих за один такт на вход кодера – k.
, поступающих за один такт на вход кодера – k.
2. Число символов на выходе кодера, соответствующих k поступившим на вход символам в течение одного такта – n.
3. Скорость (производительность) кода R, которая определяется отношением R = k/n и характеризует избыточность, вводимую при кодировании.
4. Коэффициент избыточности кода kпк = 1– R = (n – k)/n = 1 – k/n.
5. Память кода (входная длина кодового ограничения, или информационная длина кодовых блоков), которая определяется максимальной степенью
порождающего многочлена в составе порождающей матрицы G(x):
 l = k
l = k  , где
, где  – степень полинома
– степень полинома  .
.
6. Маркировка свёрточного кода: (n, k, l ). Возможны варианты.
7. Вес P двоичных кодовых последовательностей, которая определяется числом «единиц», входящих в эту последовательность или кодовый блок.
8. Кодовое расстояние di j, показывающее степень различия между i-й и
j-й кодовыми комбинациями при условии их одинаковой длины. Для любых
двух двоичных кодовых комбинаций кодовое расстояние равно числу несовпадающих в них символов.
9. Кодовое расстояние Хэмминга d для свёрточных кодов определяется следующим образом. Сверточные коды являются непрерывными и характеризуются многими расстояниями bi j, определяемыми длинами начальных сегментов кодовых последовательностей. Минимальная из величин bi j является расстоянием Хэмминга d свёрточного кода. Число символов в принятой для обработки длине сегмента на приёмной стороне определяет число ячеек регистра сдвига в декодирующем устройстве.
В качестве примера помехоустойчивого кода, исправляющего одиночные ошибки, приведём впервые предложенный в 1947 г. Хэммингом самокорректирующийся код его имени. Каждый блок этого кода имеет четыре бинарных информационных знака bi(4) = (ui1, ui2, ui3, ui4) и три проверочных (ai1, ai2, ai3), то есть классический код Хэмминга является блочным равномерным разделимым линейным кодом (7, 4) с коэффициентом избыточности kпк = 1 – 4/7 = 0,43.
Проверочные символы (ai1, ai1, ai1) формируются следующим образом:
ai1 = ui1  ui2
ui2  ui3; ai2 = ui2
ui3; ai2 = ui2  ui3
ui3  ui4; ai3 = ui1
ui4; ai3 = ui1  ui2
ui2  ui4.
ui4.
Если на декодер поступает с выхода канала КПДС кодовый блок  = = (u'i1, u'i2, u'i3, u'i4, a'i1, a'i2, a'i3), то в декодере, в режиме обнаружения и исправления одиночных ошибок, вычисляются следующие синдромы:
= = (u'i1, u'i2, u'i3, u'i4, a'i1, a'i2, a'i3), то в декодере, в режиме обнаружения и исправления одиночных ошибок, вычисляются следующие синдромы:
ci1 = a'i1  u'i1
u'i1  u'i2
u'i2  u'i3; ci2 = a'i2
u'i3; ci2 = a'i2  u'i2
u'i2  u'i3
u'i3  u'i4; ci1 = a'i3
u'i4; ci1 = a'i3  u'i1
u'i1  u'i2
u'i2  u'i4.
u'i4.
Синдром ci = (0, 0, 0) указывает на то, что в принятом кодовом блоке (u'i1, u'i2, u'i3, u'i4, a'i1, a'i2, a'i3) нет одиночных ошибок. Если ci ≠ (0, 0, 0), то декодер определяет ошибочный символ блока и исправляет его согласно следующей таблице:
| Синдром | |||||||
| Позиция ошибки | |||||||
| Ошибочн. символ | ai3 | ai2 | ui4 | ai1 | ui1 | ui3 | ui2 |
Мы уже говорили, что коэффициент избыточности kпк помехоустойчивого кода должен быть не меньше коэффициента ненадёжности канала КПДС. С другой стороны, коэффициент надёжности χ(П) каналов передачи дискретных сообщений непосредственно связан с отношением «сигнал/помеха» в линиях электросвязи современных электронных систем.
В простейшем случае симметричного бинарного канала КПДС согласно формуле (9.3):
P1 = P2 = 0,5; P11 = P22 = p и χ(П) = χ( p) = 1 + p log p + (1 – p) log(1 – p).
Если p = 1, то χ( p) = 1. Если p = 1/2, то χ( p) = 0.
Пусть в симметричном бинарном канале “единица” передаётся уровнем сигнала (+U ), “ноль” – уровнем (–U ), а помехи имеют гауссовское распределение с нулевым средним и с дисперсией σn2 (индекс n означает “noise” – шум).
Тогда
p = 
 [– (x – U )2/(2 σn2)] dx = 0,5 [1 + Φ(
[– (x – U )2/(2 σn2)] dx = 0,5 [1 + Φ(  )], (10.1)
)], (10.1)
где Φ(u) = 
 – интеграл вероятности (функция Лапласа);
– интеграл вероятности (функция Лапласа);
Q = (U/σn) 2 – отношение сигнал/помеха.
Зависимость коэффициента надёжности χ( p) симметричного бинарного канала КПДС, который вычисляется по формуле (9.3) при значении p, определяемом формулой (10.1), от величины отношения сигнал/помеха Q = (U/σn)2 приведена на рис. 11. Из рис. 11 следует, что непреднамеренные помехи практически не могут привести к полной потере информации в канале КПДС.
 χ
χ


 1
1
 0,5
0,5
 |  |



 0
0
Q
Рис. 11. Зависимость коэффициента надёжности χ
симметричного бинарного канала КПДС от отношения сигнал/помеха Q
Из рис. 11 также, например, следует: чтобы при отношении сигнал/помеха в канале КПДС симметричной бинарной системы ССПИ Q = 1 реализовать надёжную передачу двоичной информации, необходимо, чтобы избыточность kпк помехоустойчивого канального кода была не менее, чем kпк = 1 – χ ≈ 0,65. То есть к каждым 7 информационным знакам необходимо присовокупить не менее 13 проверочных символов, то есть на каждый знак – по два проверочных символа. Например, применить блочный код (3, 1). Это почти эквивалентно передаче речевого сообщения по «плохому» телефонному каналу «по буквам».
Таким образом,
| за надёжную передачу дискретных (знаковых) сообщений с помощью статической системы ССПИ, имеющей ненадёжный канал КПДС, приходится «платить» бóльшим объёмом ПЗУ, необходимым для того, чтобы записать в него не только принимаемые информационные знаки, но и соответствующее количество проверочных символов. |
Аналогичная ситуация возникает в теории надёжности: при синтезе надёжной системы из ненадёжных элементов приходится вводить соответствующую избыточность её элементов.
Кстати, в задачах различения знаков и обнаружения сигналов на фоне аддитивных шумов отношение сигнал/помеха Q играет такую же роль, как вели-
чина Ij = – log Pj в определении количества информации для семиотических (знаковых) систем.
Действительно. Пусть мы имеем некоторую выборку (последовательность) X (m) = ( u1, u2, …, uk, …, um ) из результатов измерений некоторой величины s0 в случае независимого аддитивного воздействия помех на результаты измерений: uk = s0 + nk , где nk – помеха в k-м канале с нулевым средним ( 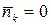 ) и с дисперсией Dk = σk2. Тогда, как это обычно бывает в современных цифровых радиосистемах передачи информации, мы имеем возможность провести накоп-
) и с дисперсией Dk = σk2. Тогда, как это обычно бывает в современных цифровых радиосистемах передачи информации, мы имеем возможность провести накоп-
ление информации об обнаруживаемом сигнале s0. Возникает вопрос: «Каким образом проводить накопление информации, чтобы получить максимально возможное суммарное отношение сигнал/помеха QΣ, которое обеспечит нам, например, максимальную надёжность бинарного канала КПДСχ( p)?»
Поскольку помехи {nk} 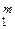 – гауссовские, то можно обрабатывать выборку
– гауссовские, то можно обрабатывать выборку
X (m) = {uk} 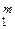 линейно, то есть можно искать оценку
линейно, то есть можно искать оценку  в виде
в виде
 =
=  uk =
uk =  s0 +
s0 +  nk при условии
nk при условии  = 1.
= 1.
Будем максимизировать величину QΣ =  , ибо суммарный сигнал sΣ =
, ибо суммарный сигнал sΣ =  , а суммарная дисперсия помех DΣ =
, а суммарная дисперсия помех DΣ = 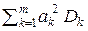 .
.
Пусть m = 2. Тогда sΣ = a1 s0 + a2 s0; DΣ = a12 D1 + a22 D2.
Поскольку a1 + a2 = 1, то a ≡ a1 = 1 – a2. Отсюда a2 = 1 – a и
sΣ = a s0 + (1 – a) s0; DΣ = a2 D1 + (1 – a)2 D2.
Значит, величина QΣ равна QΣ = [a s0 + (1 – a) s0]2/[a2 D1 + (1 – a)2 D2], а максимальное – по переменной a – значение QΣ найдётся решением уравнения dQΣ /da = 0.
В результате получаем:
a1 = 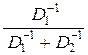 ; a2 =
; a2 = 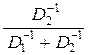 ; QΣ = s02 D1–1 + s02 D2–1 = Q1 + Q2. (10.2)
; QΣ = s02 D1–1 + s02 D2–1 = Q1 + Q2. (10.2)
Как видим, при весовых коэффициентах a1,2 = D1,2–1/(D1–1 + D2–1) результи-
тирующее отношение сигнал/помеха QΣ будет максимальным и равным просто сумме отношений Q1 и Q2. Если положить a1,2 = D1,2–1, то результирующее отношение сигнал/помеха будет тем же самым, поскольку общий множитель b ≠ 0
у весовых коэффициентов {ak} 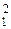 не изменяет величины QΣ:
не изменяет величины QΣ:
QΣ =  =
= 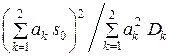 .
.
Значит, в качестве оптимальных весовых коэффициентов a1,2 в формулах (10.2) можно брать величины a1,2 = D1,2–1.
При m > 2 получаем аналогичные результаты:
 =
= 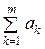 uk; ak = Dk–1; QΣ =
uk; ak = Dk–1; QΣ = 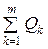 .
.
Итак,
если при регистрации дискретных сигналов {sk} 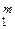 одного источника
гауссовские аддитивные помехи {nk} одного источника
гауссовские аддитивные помехи {nk} 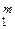 не коррелированы
между собой, то при оптимальной линейной обработке не коррелированы
между собой, то при оптимальной линейной обработке
 = =  результатов регистраций принимаемой смеси
сигналов {sk} результатов регистраций принимаемой смеси
сигналов {sk} 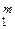 и помех {nk} и помех {nk} 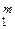 отношения сигнал/помеха {Qk = sk2/Dk} отношения сигнал/помеха {Qk = sk2/Dk} 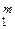 просто суммируются: QΣ =
просто суммируются: QΣ =  . .
|
В некоторых трудах по статистической радиотехнике отношение сигнал/помеха определяется как q = s/σn. При таком определении замечательное свойство аддитивности отношения сигнал/помеха Q теряется.
Таким образом, абстрактно-математические выкладки прикладной теории информации, относящиеся к семиотическим (знаковым, дискретным) статическим системам передачи информации (ССПИ) мы всегда можем связать (на основании результатов статистической теории радиотехнических систем – см., например, [42]) со статистическими характеристиками цифровых каналов радиосвязи и оценить информационную ёмкость и надёжность конкретной системы ССПИ.
Вопросы для самопроверки
1. Каким образом реализуется информационная надёжность данного канала передачи дискретных сообщений практически?
2. Что такое «байт»?
3. В чём состоит операция перемежения и для чего она используется в системах электросвязи?
4. Какова классификация помехоустойчивых кодов?
5. Что такое коэффициент избыточности помехоустойчивого кода?
6. Что такое бинарное разделимое блочное кодирование?
7. Чем определяется расстояние Хэмминга данного блочного кода?
8. Что такое кодовое расстояние данного блочного кода?
9. Чем определяется математическая группа, и каковы основные её свойства?
10. Что такое естественный базис блочного кода?
11. Какая матрица называется порождающей или производящей данный избыточный код?
12. Какова структура циклического блочного кода?
13. Что такое порождающий полином циклического блочного кода?
14. Каким образом порождающая матрица циклического блочного кода связана с порождающим его полиномом?
15. Каким образом связан коэффициент информационной надёжности симметричного бинарного канала передачи дискретных сообщений с отношением сигнал/шум в системе электросвязи?
Дата добавления: 2015-05-16; просмотров: 1153;
