С помощью многоуровневых сигналов. Проблема квантования
Как мы уже знаем (см. разд. 1 и Прил. 3), много десятилетий инженеры стремились повысить скорость передачи телеграфных сообщений самыми разными методами, в том числе и за счёт использования многоуровневой телеграфии. Т. Эдисон и Дж. Прескотт в 1984 г. изобрели четырёхуровневый телеграф, а Г. Найквист в 1924 г. рассматривал многоуровневую телеграфию теоретически. Однако технически многоуровневую телеграфию удалось реализовать только в 1990-х годах: в радиосистемах с многопозиционной амплитудной манипуляцией M-ASK. При этом модуляция M-ASK может рассматриваться как частный случай квадратурной амплитудной модуляции QAM: модуляция QAM с одномерным сигнальным созвездием.
Так мы возвращаемся (на более высоком уровне развития технических средств телекоммуникаций) к проблематике многоуровневой телеграфии, которая привела к созданию прикладной теории информации (см. разд. 1).
Рассмотрим задачу оценивания количества знаковой информации, которую может передать статическая система ССПИ многоуровневой телеграфии, использующая канал КПДС с известным уровнем аддитивных помех в канале КПДС.
Если некоторая непрерывная физическая величина (например, напряжение u постоянного тока) используется для передачи с помощью статического канала КПДС дискретной информации, то возникает вопрос о количестве необходимых уровней и расстояниях между ними (количество «чётко различимых уровней» Г. Найквиста и К. Шеннона – см. разд. 1): проблема квантованияс минимальной потерей информации.
Пусть уровни передаваемых сигналов «многоуровневого телеграфа» могут лежать в пределах от – Uт до +Uт, а погрешности определения этих уровней с помощью цифро-аналогового преобразователя (ЦАП), работающего по правилу k = [ u/Δu + 1/2 ], имеют равномерное распределение в пределах от – W до +W (W < Uт, см. рис. 14).
p(u)
2 W
U1 U2 Uk UN
– U Δu 0+ U u
Рис. 14. Распределение уровней Uk и помех pп(u)
в системе ССПИ
Разобьём промежуток (– Uт, +Uт) на N уровней с интервалом (величиной кванта) Δu так, чтобы N = 1 + 2 Uт /Δu. Если избыточность источника ДИС предварительно снята (соответствующим кодированием первичных знаков некоторыми символами vk), то все эти N уровней, соответствующие поступающим на ЦАП N символам vk (k = 1, 2, …, N ), будут равновероятными.
Как показано в разд. 10, большую роль в статистической и в информационной теориях радиосистем имеет энергетический параметр Q, называемый «отношением сигнал/помеха». В бинарной системе ССПИ он определяется как Q = U 2/σn2.
В многоуровневом телеграфе следует предварительно определить среднюю мощность сигнала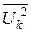 
. Если N – чётное число (см. рис. 14), то N = 2 M и
= 
,
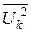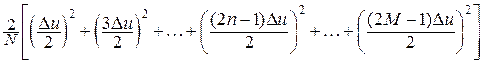или =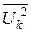 
.
Но 
= (L + 1) (2 L + 1) (2 L + 3)/3. Поэтому
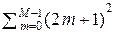= (M – 1 + 1) (2 M – 2 + 1) (2 M – 2 + 3)/3 = M (2 M + 1) (2 M – 1)/3.
Значит, 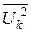= Δu2 (2 M + 1) (2 M – 1)/12.
Если учесть, что Δu = 2 Uт /(N – 1), то есть =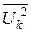 
,
то окончательно получим: =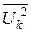 
.
Если N – нечётное, то есть N = 2 M + 1, то 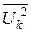= Δu 2 M (M + 1)/3 и при Δu = 2 Uт /(N – 1): = 
.
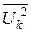Итак, при любом значении N средняя мощность сигнала определяется
выражением
= 
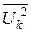. (12.1)
При N = 2 (обычный двухполярный телеграф или двухуровневая фазовая манипуляция 0º/180º – см. разд. 10) величина 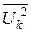= 3 Uт2/3 = Uт2, что очевидно.
При N >> 1 величина 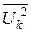≈ Uт2/3, что соответствует равновероятному закону распределения бесконечного числа уровней Uk и пределах (– Uт, + Uт) и что следует из вычисления дисперсии случайной величины α, равномерно распределённой на произвольном числовом промежутке длиной 2 Uт (см. разд. 11).
Дисперсия же помехи, равномерно распределённой на промежутке (– W, + W), равна: σn2 = W 2/3. Значит, в многоуровневом телеграфе отношение
сигнал/помеха есть: Q =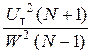 
, или Q = 
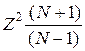, где Z ≡ Uт /W.
Если выполняется неравенство Δu > 2 W, то передача сообщений с помощью преобразователя ЦАП («многоуровневая телеграфия») будет абсолютно надёжной (Pjj = 1, χ(Π) = 1). При этом среднее количество информации 
, приходящееся на один передаваемый символ vk (k = 1, 2, …, N ), будет равно = log N = log (1 + 2 Uт /Δu) (бит/символ).
Максимальное значение N0 = 1 + Uт /W соответствует величине кванта Δu = 2 W.
При уменьшении величины кванта Δu от Δu = 2 Uт до Δu = 2 W количество уровней N = 1 + 2 Uт /Δu увеличивается от N = 2 до N = 1 + Uт /W = N0, а средняя информативность символа будет увеличиваться
от 
= log 2 = 1 до 
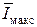= log (1 + Uт /W ) = log N0 (бит/символ).
Если же величина кванта Δu будет менее 2 W, то количество уровней N = 1 + 2 Uт /Δu будет больше величины N0, но эти уровни сигналов на выходном преобразователе ЦАП канала КПДС будут «перепутываться» и будет происходить частичная потеря знаковой информации относительно максимально возможной 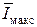при данном значении отношения Z = Uт /W, то есть относительно величины
ℰ = 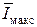= log N0 = log (1 + Uт /W ) = log (1 + Z ) = 
,
так как 1 + Q = 1 + Z 2 (1 + Z + 1)/(1 + Z – 1) = 1 + 2 Z + Z 2 = (1 + Z )2.
Среднее количество информации на один входной символ, которое получается на выходе канала КПДС при данных значениях величин Uт, Δu и W, с учётом равенства Pj = 1/N, определяется по формуле (7.4):
= 
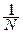
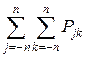log 
, (12.2)
а коэффициент надёжности
χ(N, Q) = 
/log N, (12.3)
где n = (N – 1)/2 = Uт /Δu, а Pjk – элементы переходной матрицы канала КПДС.
Если W < Δu ≤ 2 W, то будут «перепутываться» только соседние уровни (см. рис. 14) – и матрица Π = || Pjk || будет трёхдиагональной. В этом случае:
Pj j =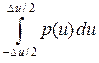 
= 
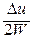; Pj, j +1 = Pj – 1, j = 
,
кроме j = – n и j = n, при которых
P11 = PNN =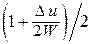 
, P12 = PN –1, N = .
Если обозначить величину Pj j = Δu /(2 W ) через p0, то
p0 = Δu /(2 W ), Pj, j+1 = P1, j–1 = (1 – p0)/2,
и матрица Π будет иметь вид
Π= 
.
Результаты расчётов по формулам (12.1) и (12.2) для канала КПДС с переходной матрицей Π приведены на рис. 15 (сплошные линии).
При N >> 1 из формулы (12.1) приближённо получаем:
= (1 – p0)/2 + p0 + (1 – p0)/2 = 1;
≈ 
=
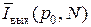= log N + p0 log p0 + (1 – p0) log (1 – p0) + p0 – 1,
а число уровней N = 1 + 2 Uт /Δu.
Если W < 2 Δu < 2 W, то матрица Π = || Pjk || будет пятидиагональной и т. д.
При Δu = 2 W = 2 
σn ≈ 3,47 σn имеем:
p0 = Δu /(2W ) = 1, N = N0, ℰ(Π) =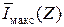 
= 
= log (1 + Z ) = log N0.
При Δu < 2 W ( p0 ≤ 1) величина 
зависит от отношения сигнал/помеха Q = Z 2 (N0 + 1)/ (N0 – 1). Общая зависимость удельной информативности 
(бит/символ) многоуровневого телеграфа (или канала КПДС с цифро-аналоговым преобразованием) от количества уровней N = 1 + 2 Zт приведена на рис. 15.а (при значениях Z = 2, 4 и 8) сплошными линиями. Величину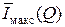 
= ≡ ℰ(Q) мы назвали (см. разд. 9) удельной информационной ёмкостью статического канала КПДС.
На рис. 16 приведена зависимость информационной ёмкости ℰ(Q) – спло-шная кривая – и оптимального количества уровней N0(Q) – пунктир – статического канала КПДС от отношения сигнал/помеха Q при уровнях {Uk} 
, равномерно распределённых в пределах от U1= – Uт до 
= + Uт, и равномерном распределении помех – в пределах от – W до + W:
ℰ(Q) = ; N0(Q) = 
.
Поскольку количество уровней не может быть менее двух, то при Q < 3 следует воспользоваться формулой (9.3) p = (W – U )/W = 1 – U/W 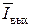= 1 – 
:
= 1 + log + (1 – ) log (1 – ).
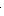χ
0,5
Z = 2 4
0
0 2 4 N0 6 8 10 N = 1 + 2 U/Δu
б )
бит 
символ
4
Log N
3
ℰ
2
1 4
Z = 2
0
0 2 4 N0 6 8 10 N = 1 + 2 U/Δu
а )
Рис. 15. Зависимость (а) удельной информативности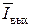
и (б) коэффициента надёжности 
: системы ССПИ
от количества уровней N = 1 + 2 U0/Δu
Значит, если задано максимально допустимое значение модуля напряжения Uт на входе статического канала КПДС и уровень W равномерно распределённых помех в канале, то при нечётном значении величины [U0/W ], где [ x ] – целая часть величины x, то есть [ x ] – максимальное целое число, не превышающее значения x, то количество «чётко различимых уровней» (термин Найквиста и Шеннона) составляет N = [1 + Uт /W ] + 1. Если элементарные сообщения источника ДИС закодированы таким образом, что полученный вторичный источник ДИСвыдаёт символы “1” и “0” независимо друг от друга и с равной вероятностью, то информационный поток “единиц” и “нолей” следует объединять в блоки размера m = [log [1 + Uт /W ]] + 1.
ℰ N0
бит
символ
4 20 ℰ(Q)
N0(Q)
3 15 3 1 2
2 10
1
 | | |
0
Q
Рис. 16. Зависимость информационной ёмкости (сплошная линия)
и оптимального количества уровней (пунктир) от величины Q
Таким образом, для передачи максимального удельного количества синтактической (дискретной) информации по аналоговому статическому каналу КПДС с равномерно распределёнными помехами нужно провести следующие операции.
1. Сообщение Si(n) = (ui1, ui2, …, uil …, uin) длины n необходимо закодировать двоичными символами (например “1” и “0”) таким образом, чтобы в любом i-м сообщении Si(n) символы “1” и “0” появлялись независимо и равновероятно (снять избыточность данного источника ДИС – см. разд. 5).
2. Исходя из допустимого на входе канала КПДС значения Uт и уровня W равномерно распределённых помех в канале определить число уровней кванто-
вания N0 = [1 + Uт /W ] при чётном n и N0 = [1 + Uт /W ] + 1 – при нечётном n.
3. Разбить поток символов “1” и “0” на последовательно идущие блоки bk длиной m = [ log N0] + 1.
4. Каждому блоку приписать значение уровня 
.
5. Подавать эти уровни напряжения (с помощью преобразователя ЦАП) на вход аналогового статического канала КПДС поблочно.
В этом случае реализуется удельная ёмкость канала КПДС
ℰ(Q) = при N0(Q) = , (12.4)
где Q – отношение сигнал/помеха: Q = Uт2 (N0 + 1)/[W (N0 – 1)].
Рассмотрим более реалистический вариант «многоуровневого телеграфа». Пусть помехи в канале КПДС распределены по гауссовскому закону с дисперсией Dn = σn2. Тогда в двухуровневой телеграфии даже при большом отношении сигнал/помеха Q = U02/Dn величина 
вых(2, Q) составляет не один бит-на-знак, а величину вых(2, Q) = χ(2, Q) = 1 + p log p + (1 – p) log (1 – p), где p = =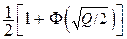 
(см. формулы (9.3), (10.1) и рис. 11).
При N > 2 для оценки величины вых(N, Q), где Q = Uт2 (N + 1)/[3 (N – 1) σn2], воспользуемся формулой (12.2), в которой N = 2 M, а при k ≠ 1 и k ≠ N элемент Pj k переходной матрицы Π есть (см. рис. 17):
Pj k = 
,
или Pj k =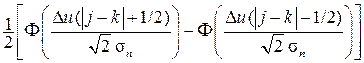 
, (12.5)
где Φ(z) – интеграл вероятности; Φ(z) = 
.
При k = 1 или k = N:
Pj k = 
. (12.6)
Результаты численных расчётов по формулам (12.6), (12.5) и (12.2) зависимости вых(Q) при N = 2, 4, 8 и 16 приведены на рис. 18.
pп(u)
Pjk
U1 U2 Uj Uk UN
– U Δu 0 + U u
Рис. 17. Распределение уровней Uk и гауссовских помех pп(u)
в статической системе ССПИ
Кривая 1 соответствует предельной ёмкости канала КПДС вых(Q) при N → ∞, которая и определяет, по существу, информационную ёмкость ℰ(Q) аналогового канала связи с ограниченной пиковой мощностью. Для проведения сравнения и аппроксимации на рис. 18 кривой 2 представлена зависимость информационной ёмкости ℰШ(Q) от отношения сигнал/помеха Q аналогового канала связи при ограниченной средней мощности – пунктир: ℰШ(Q) 
(формула Шеннона, которую мы упоминали в разд. 1 и которую выведем в разд. 13).
При больших значениях Q (Q ≈ 1000) величина ℰШ(Q) на 0,23 (бит/сим-вол) больше, чем величина, даваемая зависимостью ℰ(Q), которую, следовательно, можно аппроксимировать функцией ℰ(Q)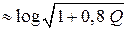 
.
Имея серию результатов расчёта величины вых(Q) при различных значениях N, можно построить аппроксимацию зависимости вых(Q) как поверхности над плоскостью {Q, N }. Для наглядности эту поверхность вых(Q, N ) при квазинепрерывном N можно представить её сечениями при значениях вых = = 1, 2, 3 и т. д. (бит/символ) – по аналогии с рельефом местности на топографи-
вых
бит
символ
4 21 16
3 8
2 4
1 N = 2
| | | |
0
Q
Рис. 18. Зависимости величины вых от отношения сигнал/помеха Q
при различных значениях количества уровней N
ческих картах (см. рис. 19). А уже по аппроксимации вых(Q, N ) для квазинепрерывного N можно делать разнообразные практические выводы.
Например. Для конечных значений N < ∞ и при заданной величине Uт: чем больше будет величина кванта Δu = 2 Uт /(N – 1), тем меньше будет число уровней квантования (телеграфной линии) N, но тем меньше будет величина
вых. Получается задача на оптимизацию величины кванта Δu, и для выбора оптимального значения Δu0 следует задаться соответствующим критерием; например «ёмкость/стоимость».
Чтобы довести рассматриваемый пример до конкретных числовых результатов, нужно при каждом значении вых = 
, 
, … построить зависимость величины приведённого кванта q0 ≡ Δu/σn от величин Q и N.
Для каждой кривой N(Q)|I = 1, 2, 3, … можно построить связанную с ней зави-
Nq0 = Δu/σn
40 8 I = 1 2 3
30 6
| | |
20 4 q0(Q)|I= 1 q0(Q)|I= 2 q0(Q)|I= 3
| |  | | |
10 2
 | |||
| | |||
0
Q
Рис. 19. Рельеф функции вых (N, Q) и выбор
оптимального количества уровней N 0 многоуровневого телеграфа
симость величины приведённого кванта q0 ≡ Δu/σn от значения Q:
U = Δu (N – 1)/2; Q =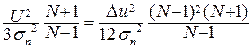 
.
Значит, q0 =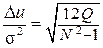 
.
На рис. 19 эти зависимости q0(Q) показаны пунктиром.
Так, согласно рис. 18, при = 1: N = 4, Q = 4,2; q0 = 1,9; N = 8, Q = 3,8; q0 = 0,85; N = 16, Q = 3,3; q0 = 0,395; при = 2: N = 8, Q = 24; q0 = 2,4; N = 16, Q = 21; q0 = 0,99 и т. д.
Если значение q0 выбрать, например, таким образом, чтобы гауссовская плотность вероятности аддитивных помех была бы эквивалентна равномерной плотности pр(x) со значением pр(0) = pn(0), то для нахождения величины Δu по-
лучаем равенство: Δu0 pn(0) = 
= 1.
Значит,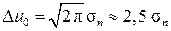 
, а Pj j ≈ 0,788 при j ≠ 1 и j ≠ N. Величину вых
при значении 
назовём практической информационной ёмкостью многоуровневого телеграфа и обозначим через ℰпр(Q).
Результаты расчётов зависимостей от отношения сигнал/помеха Q вели-
чины практической информационной ёмкости ℰпр и соответствующей ей оптимального количества уровней квантования N0 при Δu0 = 2,5 σn (процесс нахождения N0 показан стрелками на рис. 19) приведены на рис. 20.
ℰпр N0
бит
символ
4 40 31
3 30 2
| |  |
2 20 ℰ(Q)|N = 2
1 10 N=2
 | | |
0
Q
Рис. 20. Зависимости от отношения сигнал/помеха Q
величины ℰпр и количества уровней N0
Кривая 1 показывает зависимость от отношения сигнал/помеха Q величины ℰпр для рассматриваемого канала КПДС, а кривая 2 – соответствующее величине ℰпр количество уровней N0.
Для проведения сравнения и аппроксимации на рис. 20 также приведена зависимость информационной ёмкости аналогового статического канала связи
ℰШ(Q), соответствующая формуле Шеннона (кривая 3).
Как видим, при больших значениях Q (Q >> 8) значение ℰпр одномерного
цифрового канала КПДС («многоуровневого телеграфа») на 0,45 (бит/символ) меньше, чем ёмкость аналогового канала с ограниченной средней мощностью
ℰШ. Поэтому зависимость вых(Q) при Δu0 = 2,5 σn можно аппроксимировать функцией: ℰпр(Q) ≡ 
при аппроксимации опти-
мального количества уровней квантования кривой 
≈ 
.
Поскольку количество уровней в телеграфе не может быть меньше, чем
два, то при Q ≤ 3 величина ℰпр(Q) определяется формулой (9.3) – см. рис. 11. На
рис. 20 показаны полные зависимости величин ℰпр и N0 от отношения сигнал/помеха Q, а на рис. 21 приведена полная зависимость от величины Q коэф-
фициента информационной надёжности χ = ℰпр /log N0 системы передачи дис-
кретных сообщений при использовании многоуровневой симметричной амплитудной манипуляции M-ASK. Пунктиром на рис. 20 показана информационная ёмкость двухуровневого телеграфа (N = 2).
χ
1
| | | |
0
1 3 10 30 100 300 Q
Рис. 21. Зависимость коэффициента информационной надёжности χ
системы передачи сообщений с симметричной модуляцией M-ASK
от величины Q
Вопросы для самопроверки
1. Каким образом вычисляется средняя мощность многоуровневого сигнала?
2. Каким образом вычисляется информационная ёмкость канала электросвязи с ограниченной пиковой мощностью при аддитивных равномерно распределённых помехах в канале?
3. Какова зависимость информационной ёмкости и оптимального количества уровней канала электросвязи с ограниченной пиковой мощностью от величины отношения сигнал/шум в канале в случае гауссовского шума?
4. Какова методика вычисления теоретической и практической информационной ёмкости, а также оптимального количества уровней и коэффициента информационной надёжности канала электросвязи с ограниченной пиковой мощностью в канале?
Дата добавления: 2015-05-16; просмотров: 962;