Пропускная способность каналов электросвязи
В части I«Информационная статика» рассматривались задачи прикладной теории информации (ПТИ), в которых фактор времени в системах передачи информации не играл существенной роли. Перейдём к учёту фактора времени.
Пусть источник знаковых (дискретных) сообщений ДИС и канал передачи дискретных сообщений КПДС работают в режиме реального времени. Тогда возникают задачи оценивания скорости выдачи динамическим источником ДИС информации – производительности динамического источника дискретных сообщений B(U)*)[бит/(знак ∙с)] и оценивания максимальной скорости передачи информации по каналу КПДС(с помехами и без них), то есть задача оценивания пропускной способности динамического канала КПДС C(П)*) [бит/(знак ∙с)], а также задача согласования этих скоростей.
В письменной знаковой системе мы имеем: алфавит данного языка плюс цифры плюс знаки препинания плюс пробел, знак отступа (абзаца), знак перевода строки и т. п. Оператор системы связи с помощью клавиатуры или сканера вводит письменный текст в канал КПДС – обычно с равномерной скоростью (знаков-в-секунду). Речевое сообщение обычно имеет различную длительность отдельных фонем, которые воспринимаются анализатором речи.
 С другой стороны, канал КПДС передаёт (с помощью, например, электрических сигналов) кодовые слова, символы которых могут иметь различную длительность соответствующих им сигналов. Например, код Морзе имеет по существу пять символов различной длительности: “точка” – длительностью τ0, “тире” – 3τ0, «интервал между “точками” и (или) “тире”» – τ0, «интервал между буквами и (или) цифрами» – 3τ0, «интервал между словами» – 5τ0. Вместе с тем, динамический канал КПДС может использовать для передачи информации, например, двухуровневые посылки (+ Uт и – Uт) одинаковой длительности.
С другой стороны, канал КПДС передаёт (с помощью, например, электрических сигналов) кодовые слова, символы которых могут иметь различную длительность соответствующих им сигналов. Например, код Морзе имеет по существу пять символов различной длительности: “точка” – длительностью τ0, “тире” – 3τ0, «интервал между “точками” и (или) “тире”» – τ0, «интервал между буквами и (или) цифрами» – 3τ0, «интервал между словами» – 5τ0. Вместе с тем, динамический канал КПДС может использовать для передачи информации, например, двухуровневые посылки (+ Uт и – Uт) одинаковой длительности.
*) B(U) – от английского слова “bearer” – податель сообщений,
C(П) – от английского слова “carrying capacity” – пропускная способность.
Назначение динамического канала КПДС: передача в режиме реального времени поступающих на вход канала КПДС сообщений с максимальной информационной скоростью и надёжностью, но – с допустимой задержкой (на снятие информационной избыточности источника ДИС, на канальное кодирование и декодирование сообщений, на формирование соответствующих последовательностей сигналов и их демодуляцию).
Информационную математическую модель динамического источника ДИСи динамического канала КПДС можно построить на основе статических моделей, дополнив эти модели длительностями элементарных сообщений (знаков) источника ДИС и длительностями элементарных посылок (сигналов) канала КПДС.
Простейшая модель динамического источника ДИС, таким образом, должна содержать совокупность из пяти множеств {U, P, I, S, T}, где U, P, I, S – известные из информационной статики множества (см. разд. 4), а T = {tj} 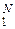 – множество длительностей tj ( j = 1, 2, …, N ) выдачи источником ДИС элементарных сообщений (первичных знаков) uj ( j = 1, 2, …, N ).
– множество длительностей tj ( j = 1, 2, …, N ) выдачи источником ДИС элементарных сообщений (первичных знаков) uj ( j = 1, 2, …, N ).
Если источник ДИСвыдал i-е сложное сообщение (текст) Si(n) = (ui1, ui2, …, uik, …, uin) длиной n, то это сообщение будет иметь длительность
Ti(n) = ti1 + ti2 + … + tik + … + tin.
При n >> 1 количество информации, произведённое источником ДИС, есть: I(Si(n)) ≈ n  (U), или I(Si(n)) ≈ – n
(U), или I(Si(n)) ≈ – n 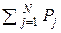 logPj ≡ n H(U).
logPj ≡ n H(U).
При тех же условиях: Ti(n) ≈ n 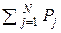 tj = n
tj = n 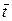 , где
, где 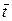 (секунда/знак) – средняя длительность элементарного сообщения (знака) из множества U = {uj}
(секунда/знак) – средняя длительность элементарного сообщения (знака) из множества U = {uj} 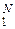 :
:
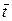 =
= 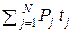 .
.
Значит, среднюю скорость выдачи информации (производительность) B(U) динамического источника ДИС можно определить как
B(U) = 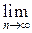
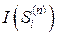 /Ti(n) =
/Ti(n) = 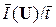 ≡ H(U) /
≡ H(U) / 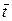 (бит/с).
(бит/с).
Рассмотрим бинарный источник ДИС, который характеризуется множествами:
U = {u1, u2}, P = {P, 1 – P}, I = { – log P, – log (1 – P)}, T = {t1, t2; t2 ≥ t1},
то есть знак u1 передаётся по динамическому каналу КПДС посылкой тока длительностью t1 (“точка”), а знак u2 – длительностью t2 (“тире”).
Производительность такого источника ДИС
R(P, t1, t2) = 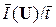 = – [ P log P + (1 – P) log (1 – P)]/[t1 P + t2 (1 – P)].
= – [ P log P + (1 – P) log (1 – P)]/[t1 P + t2 (1 – P)].
Какова максимальная производительность источника ДИС при заданных значениях t1 и t2?
Введём среднеарифметическую длительность посылок tса = (t2 + t1)/2 и относительное отклонение δ = (t2 – t1)/(t2 + t1); 0 ≤ δ ≤ 1; их длительностей от среднеарифметического. Тогда
B(P, tса, δ) = 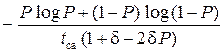 .
.
При заданных значениях tса и δ величина максимальной производительности Bмакс(tса, δ) бинарного источника ДИС определится значением P0, которое находится из уравнения
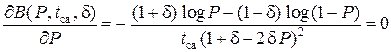 ,
,
или (1 + δ ) log P = ( 1 – δ ) log (1 – P). (15.1)
Отсюда получаем уравнение
P0(1 + δ) = (1 – P0)(1 – δ). (15.2).
Уравнение (15.2) – трансцендентное и оно может быть приближённо решено графически, а его точное решение можно получить из приближённого с помощью итерационного вычислительного процесса. Поэтому – с учётом соотношения (15.1) – получаем:
Bмакс(tса, δ) = 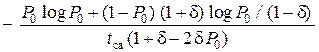 =
= 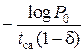 .
.
Величина 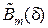 = tса Bмакс(tса, δ) (при заданном значении tса) зависит только от величины δ = (t2 – t1)/(t2 + t1). Зависимость десятичного логарифма величи-
= tса Bмакс(tса, δ) (при заданном значении tса) зависит только от величины δ = (t2 – t1)/(t2 + t1). Зависимость десятичного логарифма величи-
 ны
ны 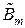 от значения величины δ приведена на рис. 24.
от значения величины δ приведена на рис. 24.


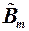
 1,5
1,5
 1,4
1,4
 1,3
1,3
 1,2
1,2

 1,1
1,1
1,04












 1
1
0 δм 0,5 1 δ
Рис. 24. Зависимость приведённой информационной производительности 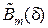 бинарного динамического источника ДИС
бинарного динамического источника ДИС
от относительной разности длительностей элементарных посылок δ
Если в коде Морзе пренебречь паузами между словами и предложениями, то по существу в нём останется два элементарных сообщения (знака):
uк – короткий символ (“точка” или “пауза между точками и (или) тире”: t1 = 2 τ0;
uд – длинный символ (“тире” или “пауза между буквами”: t2 = 4 τ0).
В таком случае: tса = 3 τ0, δМ = 1/3, P0 ≈ 0,618; 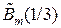 ≈ 1,04 (см. рис. 24).
≈ 1,04 (см. рис. 24).
Значит, чтобы реализовать максимальную производительность источника ДИС U = {uj} 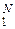 (N ≥ 2) с помощью кода Морзе, нужно так закодировать алфавит U = {uj}
(N ≥ 2) с помощью кода Морзе, нужно так закодировать алфавит U = {uj} 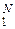 , чтобы в длинных сообщениях Si(n) (n >> 1) короткие символы появлялись в P0/(1 – P0) ≈ 0,618/0,382 ≈ 5/3 раз чаще, чем длинные. Производительность такого источника (Морзе) BМ = 1,04/(3 τ0) = 0,347/τ0 (бит/с).
, чтобы в длинных сообщениях Si(n) (n >> 1) короткие символы появлялись в P0/(1 – P0) ≈ 0,618/0,382 ≈ 5/3 раз чаще, чем длинные. Производительность такого источника (Морзе) BМ = 1,04/(3 τ0) = 0,347/τ0 (бит/с).
Если же использовать биполярные посылки постоянного тока одинаковой
длительности (положительная посылка + пауза = “точка”, отрицательная + пауза = = “тире”), то производительность такого источника (симметричной двухуровневой телеграфии) Bдп = 1/(2 τ0) = 0,5/τ0 (бит/с).
В современных системах подвижной радиосвязи используется бинарная фазовая 0º/180º или частотная манипуляция, при которой пауз между посылками не требуются; значит, в системах электросвязи с двухпозиционной манипуляцией Bдм = 1/τ0 (бит/с).
В цифровых транкинговых системах радиосвязи стандарта TETRA и в системах связи III поколения стандарта cdma 2000 3 x используется четырёхпозиционная фазовая манипуляция (π/4, 3π/4, – 3π/4, – π/4). В таких системах BТ = 2/τ0 (бит/с).
В радиосистемах III поколения стандарта EDGE предусмотрена восьмипозиционная фазовая манипуляция; в них производительность BE = 3/τ0 (бит/с).
В радиосистемах IV поколения будет предусмотрена 64-позиционная квадратурная амплитудная модуляция (64-QAM ); в них BIV = 6/τ0 (бит/с). В некоторых системах радиосвязи используется 256-QAM.
Таким образом, относительную производительность источников знаковых сообщений (ДИС) за последние 170 лет удалось повысить с 1/(3τ0) в 1838 г. до 8/τ0 – в 2010-12 годах, то есть «всего лишь» в 24 раза.
В общем случае динамических источников ДИС (N > 2) максимальной производительностью будут обладать источники, у которых все знаки – равновероятны, а длительности соответствующих им посылок (тока или напряжения) – одинаковы.
Пусть динамический канал КПДС без помех передаёт информацию с помощью символов vr (r = 1, 2, …, M ), которым соответствуют некоторые сигналы sr. Максимальное количество информации, приходящейся на один из множества символов V = {vr} 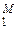 , которые имеют длительности {τr}
, которые имеют длительности {τr} 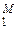 , будет иметь место тогда, когда символы vr – равновероятны: H(V) = log M. В этом случае средняя скорость передачи информации в канале КПДС определяется равенством H(V)/
, будет иметь место тогда, когда символы vr – равновероятны: H(V) = log M. В этом случае средняя скорость передачи информации в канале КПДС определяется равенством H(V)/ 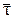 = (log M )/
= (log M )/ 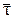 . Максимальная скорость передачи информации (пропускная способность) канала КПДС:
. Максимальная скорость передачи информации (пропускная способность) канала КПДС:
C(П) = (log M ) / 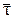 [бит/с], где
[бит/с], где 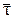 =
= 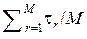 .
.
Если τr = τ (r = 1, 2, …, M ), то Pr = P = 1/M и C(П) = (log M ) /τ.
Ясно, что если B(U) ≤ C(П), то данный динамический канал без помех может (практически без искажений) передавать знаковую (дискретную) информацию, производимую данным динамическим источником ДИС.
При B(U) ≤ C(П): (log M ) /τ = H(U) / 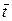 , или H(U) /log M =
, или H(U) /log M = 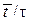 .
.
Но величина H(U)/log M есть (теоретическая) средняя длина кодового слова 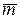 (символ/знак). Отсюда следует, что для надёжной передачи информации, производимой динамическим источником ДИС со средней скоростью B(U) = H(U)/
(символ/знак). Отсюда следует, что для надёжной передачи информации, производимой динамическим источником ДИС со средней скоростью B(U) = H(U)/ 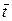 (бит/с), посредством динамического каналаКПДС с пропускной способностью C(П) = (log M )/τ (бит/с), необходимо выполнение неравенства B(U) ≤ C(П), или
(бит/с), посредством динамического каналаКПДС с пропускной способностью C(П) = (log M )/τ (бит/с), необходимо выполнение неравенства B(U) ≤ C(П), или 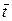 ≥ (τ
≥ (τ 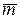 ), или
), или 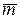 ≤ (
≤ ( 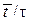 ), где
), где 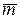 = H(U)/log M – средняя длина кодовых слов [размерность – (символ/знак)], получаемых при оптимальном кодировании элементарных сообщений источника ДИС. И хотя канал КПДС без помех имеет теоретическую надёжность χ(П) = 1, всё же потери информации при передаче по нему дискретных сообщений будут происходить – в силу ограниченности допустимой задержки и ограниченного объёма оперативного запоминающего устройства.
= H(U)/log M – средняя длина кодовых слов [размерность – (символ/знак)], получаемых при оптимальном кодировании элементарных сообщений источника ДИС. И хотя канал КПДС без помех имеет теоретическую надёжность χ(П) = 1, всё же потери информации при передаче по нему дискретных сообщений будут происходить – в силу ограниченности допустимой задержки и ограниченного объёма оперативного запоминающего устройства.
Действительно. В некоторых сложных сообщениях Si(n) иногда могут следовать подряд несколько очень редких элементарных сообщений uj 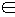 U, которые содержат большое количество информации. Для их оптимального кодирования будут использоваться соответствующие им очень длинные кодовые слова (длиной mj ≈ – log Pj /log M ), на формирование которых потребуется интервал времени Δt, приблизительно равный Δt ≈ mj τ. Значение Δt может превысить допустимую задержку в передаче информации, что и вызовет потерю некоторого количества информации. Кроме того, пока эти знаки кодируются, необходимо запоминать в ОЗУ следующие за ними знаки, непрерывно выдаваемые источником ДИС, что может привести к переполнению ОЗУ.
U, которые содержат большое количество информации. Для их оптимального кодирования будут использоваться соответствующие им очень длинные кодовые слова (длиной mj ≈ – log Pj /log M ), на формирование которых потребуется интервал времени Δt, приблизительно равный Δt ≈ mj τ. Значение Δt может превысить допустимую задержку в передаче информации, что и вызовет потерю некоторого количества информации. Кроме того, пока эти знаки кодируются, необходимо запоминать в ОЗУ следующие за ними знаки, непрерывно выдаваемые источником ДИС, что может привести к переполнению ОЗУ.
Итак, в динамической системе передачи дискретной (знаковой) информации происходит следующее.
● Динамический источник ДИС производит (выдаёт) сложные знаковые сообщения Si(n) 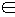 S со средним темпом
S со средним темпом 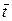 (секунда/знак), то есть со средней «фи-
(секунда/знак), то есть со средней «фи-
зической» скоростью 1/ 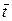 (знак/с).
(знак/с).
● Динамический канал КПДС передаёт символы sr 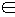 K посредством сигналов со средней длительностью (элементарной посылки)
K посредством сигналов со средней длительностью (элементарной посылки) 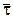 (секунда/символ).
(секунда/символ).
● Среднее количество информации, производимое источником ДИС в секунду, то есть информационная производительность ДИС, есть:
B(U) = H(U)/ 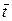 (бит/с).
(бит/с).
● Максимальная средняя скорость передачи информации по динамическому каналу КПДС, то есть его пропускная способность, есть:
C(П) = (log M )/τ (бит/с).
● Кодер источника ДИС снимает избыточность источника (при оптимальном кодировании элементарных сообщений) с помощью символов канала КПДС.
● Средняя задержка выдачи в канал КПДС информации складывается из среднего времени выдачи 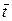 источником ДИСэлементарных сообщений и среднего времени оптимального их кодирования (
источником ДИСэлементарных сообщений и среднего времени оптимального их кодирования ( 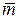 τ). Разброс задержек иногда может превысить допустимую величину – и часть информации источника ДИС может потеряться.
τ). Разброс задержек иногда может превысить допустимую величину – и часть информации источника ДИС может потеряться.
● Чтобы в ОЗУ кодера динамического источника ДИС не накапливались (до бесконечности) выдаваемые источником ДИС знаковые сообщения, необходимо выполнение неравенства 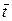 ≥ (
≥ ( 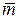 τ).
τ).
Таким образом, мы получили следующий результат (основная теорема Шеннона для «дискретного канала без шума», [46], с. 270).
| «Пусть источник имеет энтропию H (бит на символ)[бит на первичный знак – Г. Х.], а канал имеет пропускную способность C (бит в секунду). Тогда можно закодировать сообщения на выходе источника таким образом, чтобы передавать символы [знаки – Г. Х.] по каналу со средней скоростью (C/H – ε) символов [знаков источника ДИС– Г. Х.] в одну секунду, где ε – сколь угодно мало. Передавать со средней скоростью бóльшей, чем C/H, невозможно». |
В наших обозначениях: C(П)/B(U) – ε.
Если в динамическом канале КПДС присутствуют помехи, то он будет иметь надёжность 0 < χ(П) < 1, а пропускная способность канала КПДС уменьшится, по сравнению со случаем χ(П) = 1, до величины
C'(П)= χ(П) C(П) = χ(П) (log M )/τ [бит/(знак ∙с)].
Поэтому для надёжной передачи знаковой (дискретной) информации по такому каналу КПДС среднюю «физическую скорость» выдачи элементарных сообщений 1/ 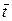 (знак/с) источника ДИС следует уменьшить относительно случая χ(П) = 1, а разность (
(знак/с) источника ДИС следует уменьшить относительно случая χ(П) = 1, а разность ( 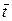 –
– 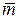 τ) – использовать для соответствующего помехоустойчивого кодирования выдаваемых в динамический канал сообщений.
τ) – использовать для соответствующего помехоустойчивого кодирования выдаваемых в динамический канал сообщений.
Отсюда вытекает основная теорема для дискретного канала с помехами ([46], с. 281):
| «Пусть дискретный канал обладает пропускной способностью C [точнее C' = χ( П ) C – Г. Х.], а дискретный источник – энтропией в секунду H {производительностью B [бит/( знак ∙с)] – Г. Х.}. Если H ≤ C [B ≤ C' – Г. Х.], то существует такая система кодирования, что сообщения источника могут быть переданы по каналу с произвольно малой частотой [частотностью – Г. Х.] ошибок (или со сколь угодно малой ненадёжностью [остаточной неопределённостью – Г. Х.])». |
Кроме того:
«Если H > C [B > C' –Г. Х.], то можно закодировать источник ДИС
таким образом, что информационная ненадёжность будет меньше,
чем (H – C + ε), где ε – сколь угодно мало.
Не существует способа кодирования, обеспечивающего ненадёжность
[остаточную неопределённость – Г. Х.] меньшую, чем ( 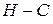 )». )».
|
То есть при B > C' в динамическом канале КПДС с помехами будет ежесекундно теряться не менее (B – C' ) [бит/знак] информации.
Всё это – абстрактно-теоретические соображения. Для практической реализации двух последних утверждений необходимо (в динамической системе передачи информации) на входе динамического канала КПДС поставить кодер канала, а на выходе канала КПДС – декодер, работающий в режиме реального времени, а также применить в системе помехоустойчивое кодирование с избыточностью не меньшей, чем ненадёжность канала КПДС.
Таким образом,
| за надёжную передачу дискретных (знаковых) сообщений с помощью динамической системы ССПИ, имеющей ненадёжный канал КПДС, приходится «платить» бóльшей символьной скоростью передачи, которая необходима для того, чтобы успевать принимать не только передаваемые информационные знаки, но и соответствующее количество проверочных символов. |
В следующем разделе мы рассмотрим аналоговые динамические каналы электросвязи.
Вопросы для самопроверки
1. Какова простейшая математическая модель динамического источника дискретных сообщений?
2. Что такое производительность динамического источника дискретных сообщений?
3. Какова максимальная производительность бинарного динамического источника дискретных сообщений?
4. Каким образом передаётся дискретная информация в динамической системе передачи информации в отсутствие помех?
5. Как формулируется основная теорема Шеннона информационной динамики для дискретного канала без помех?
6. Как формулируется основная теорема Шеннона информационной динамики для дискретного канала при наличии в канале помех?
Дата добавления: 2015-05-16; просмотров: 902;
