Формула Шеннона и интервал Найквиста

Развитие телеграфной техники привело к необходимости теоретически оценить предельно достижимую скорость передачи элементарных посылок тока через канал связи, рассматриваемый как линейный фильтр нижних частот с частотой среза F_н (Проблема № 3 ПТИ). Первым, кто в 1928 г. успешно решил эту задачу, был американский электроинженер шведского происхождения Гарри Найквист. Он доказал, что интервал между соседними элементарными телеграфными посылками T_э должен быть не менее, чем величина 1/(2 F_н): T_э ≥ 1/(2 F_н). Подчеркнём, что при аналого-цифровом преобразовании сигналов s(t) со спектром, ограниченным величиной F_m, величина интервала дискретизации Δt_д, напротив, должна быть не более, чем величина 1/(2 F_m): Δt_д ≥ 1/(2 F_m).

По предложению Шеннона предельное значение интервала (шага, периода) дискретизации Δt_макс = 1/(2 F_m), где F_m – максимальное значение частоты финитного спектра 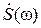детерминированного сигнала s(t) с ограниченной энергией или энергетического спектра W_ξ(ω) эргодического случайного сигнала ξ(t), называется интервалом Найквиста (см. разд. 15), хотя сам Найквист проблемой дискретизации не занимался. Однако рассуждения Г. Найквиста относительно предельно достижимой скорости телеграфирования оказались настолько логически безукоризненными и нашли такое широкое применение в современных цифровых системах электросвязи, что они безусловно должны войти в курс «Прикладная теория информации» как пример глубокого инженерного подхода к математическим проблемам.

В 1924 г. Г. Найквист опубликовал статью «Некоторые факторы, влияющие на скорость телеграфирования» [53], в которой он сформулировал эвристическое положение (p. 332-333): «Скорость, с которой сообщение может передаваться по телеграфной линии, имеющей заданную … частоту следования элементарных посылок, может быть определена приблизительно следующей формулой … W = K log m, где W – скорость передачи сообщения, m – число уровней тока [используемых в многоуровневой телеграфии – Г. Х.], – константа».

Отметим, что в 1924 г. Найквист пользуется термином “intelligence” (сообщение), а не “information” (информация).

Вместе с тем, величина K в формуле Найквиста должна зависеть от частоты среза F_Н полосы пропускания телеграфной линии, рассматриваемой как фильтр нижних частот, поскольку элементарные посылки тока претерпевают в проводной линии связи соответствующие линейные искажения: затягивание фронтов импульсов тока, наличие у телеграфных сигналов на выходе линии связи «хвостов» и т. п.

Сотрудник Найквиста по Белловским телефонным лабораториям Ральф Хартли в 1928 г., на основании анализа переходных процессов в телеграфнойсистеме, пришёл к следующем качественному выводу (цит. по рус. переводу [50], с. 24): «… максимальная скорость передачи информации, возможная в системе, частотный диапазон которой ограничен некоторой областью [не обязательно частотой среза по низким частотам – Г. Х.], пропорциональна ширине этой полосы частот. Отсюда и следует, что о б щ е е к о л и ч е с т в о и н ф о р м а -ц и и, к о т о р о е м о ж е т б ы т ь п е р е д а н о п о с р е д с т в о м т а к о й с и ст е м ы, п р о п о р ц и о н а л ь н о п р о и з в е д е н и ю п е р е д а в а е -

м о й п о л о с ы ч а с т о т н а в р е м я, в т е ч е н и е к о т о р о г о с и с т е-м а и с п о л ь з у е т с я д л я п е р е д а ч и» [разрядка Р. Хартли – Г. Х.]. Кроме того, он считает, что следующую элементарную посылку нужно передавать тогда, когда переходные процессы в телеграфной линии практически уже затухли. Подчеркнём, что в 1928 г. Хартли использует уже термин “information” и обобщает меру количества информации, предложенную Найквистом (log m) для случая равновероятных дискретных сообщений.

В фундаментальной статье 1928 г. [54] Г. Найквист пишет (p. 617): «Чтобы определить степень искажения телеграфных сигналов, нужно рассчитать переходные процессы в телеграфной системе. Эта методика использовалась различными авторами [в том числе и Хартли – Г. Х.], а их решения справедливы для телеграфных систем с простыми начальными условиями ...

Статья “атакует” эту же проблему с альтернативной точки зрения: с использованием характеристик установившегося режима в системе».

Вначале Найквист рассматривает «многоуровневую телеграфию», при которой длительности подряд идущих элементарных прямоугольных посылок одинаковы и равны τ_э, а каждая элементарная посылка имеет свой индивидуальный множитель a_h. Если взять N таких телеграфных посылок, то спектр Фурье последовательности посылок с амплитудами a₁, a₂, …, a_h, …, a_N будет линейчатым и определяться «фактором формы»:

F( f_n) = 2 sin (π f_n τ_э)/(π f_n τ_э) = 2 sinc (π f_n τ_э), где sinc (x) ≡ (sin x)/x.

Наоборот, если имеется элементарная посылка, спектр которой является равномерным в полосе частот f от f = 0 до f = F_Н, а вне этой полосы – нулевой, то её форма есть s_э(t) = 2 F_Н sinc (2 π F_Н t). Позже эту функцию назвали функцией отсчётов (см. разд. 15).

При t = 0 величина s_э(0) = 2 F_Н, а при t_k = k/(2 F_Н); k ≠ 0; величина s_э(t_k) = 0. Отметив этот математический факт, Найквист переходит к анализу сигналов во временнόй области.

Телеграфный канал в первом приближении можно считать фильтром нижних частот с частотой среза F_Н. Поэтому на выходе системы сигнал s_вых(t) по отношению к входной прямоугольной посылке длительностью τ_э будет «затянутым», и часть энергии предыдущих элементарных посылок будет попадать в интервал времени, отведённый для текущего элемента, что вынуждает уменьшать скорость телеграфирования (скорость поступления на вход телеграфного канала элементарных посылок), то есть подавать элементарные посылки с частотой (0,5 ... 0,7) F_Н, что характерно для обычного однополюсного двухуровневого телеграфа.

Как истинный инженер-изобретатель, Найквист вводит неожиданный, но почти очевидный критерий отсутствия межсимвольных искажений. Он замечает, что если на выходе телеграфной линии, на которую поступают прямоугольные (элементарные) посылки с различными амплитудами из множества 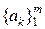(многоуровневая телеграфия), измеряются мгновенные напряжения (или токи) в середине каждой посылки и если измеренные напряжения будут пропорциональны этим амплитудам, то на выходе канала можно будет синтезировать последовательности прямоугольных посылок, подобные входным последовательностям. В таком случае, несмотря на межсимвольную интерференцию, имеющуюся на выходе телеграфной линии с ограниченной полосой пропускания F_Н, передача сообщений будет неискажённой.

В Прил. II-А к статье [54] Найквист показывает, что такому критерию удо-влетворяют сигналы, которые имеют равномерную амплитудно-частотную характеристику в диапазоне частот f от f = 0 до f = F_Н, то есть s_вх(t) = a_h sinc (π t /τ_э), где τ_э = 1/(2 F_Н). На выходе канала связи с равномерным коэффициентом передачи 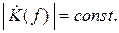в полосе частот f от f = 0 до f = F_Н вклад всех элементарных посылок, предшествующих данной посылке, в середине временного интервала, который соответствует текущей посылке, будет нулевым, и межсимвольных искажений не будет.

Такие телеграфные системы – нереализуемы. Однако Найквист доказывает, что если к сигналу с идеальной прямоугольной амплитудно-частотной характеристикой (АЧХ) добавить сигнал, спектр которого симметричен относительно F_Н(с точностью до знака), то получившийся суммарный телеграфный сигнал также не будут вносить межсимвольных искажений и будет передавать сообщения со скоростью v_т, близкой к величине 2 F_Н, что в 2-3 раза превышает скорость телеграфирования в обычном (однополярном) телеграфе. Правда, для этого в телеграфной системе должна производиться сложная синхронная нелинейная обработка сигналов, что было реализовано лишь в 1980-х годах в системах электросвязи с многоуровневой амплитудной манипуляцией N-ASK.

На рис. 27 представлены действительные и мнимые части коплексных спектров телеграфной волны (элементарной посылки), которая позволяет пере-

давать телеграфные сообщения с максимальной скоростью телеграфирования

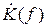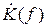по телеграфной линии связи без помех, имеющей коэффициент передачи вида: = 1 при | f | >> F_Н. Рис. 27.а соответствует идеальному телеграфному сигналу s_вх(t) с прямоугольной амплитудно-частотной характеристикой и с физически не реализуемой формой s_вх(t) = A sinc (2 π F_Н t).

На рис. 27.б и 27.в представлены соответственно действительные и мнимые части спектра сигнала, имеющего нулевые переходы в точках: t_k = k /(2 F_Н), где k = 0, ± 1, ± 2, … На рис. 27.г – действительная часть спектра суммарного сигнала s_вх(t), который может быть передан по рассматриваемой телеграфной линии с максимальной скоростью телеграфирования v_т = 2 F_Н. Покажем, что добавочный сигнал s₊(t) , который имеет «кососимметричную» реальную 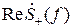и симметричную относительно точки f = F_Н мнимую части спектра , изображённые на рис. 27.б, не будет вносить линейных искажений в значения сигнала s_вх(t) = A sinc (2 π F_Н t) в точках t_m = m /(2 F_Н) = m /τ_э.

Действительно. Выделим в спектре сигнала s₊(t) элементарные полосы частот шириной Δ f около частот f_+n = F_Н + n Δ f и f_{– n} = F_Н – n Δ f ; n ≠ 0.

Получим элементарные колебания:

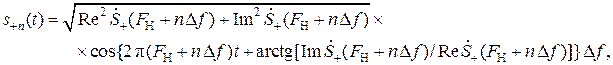
По построению (см. рис. 27.б) имеем:

,

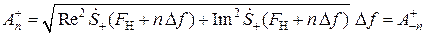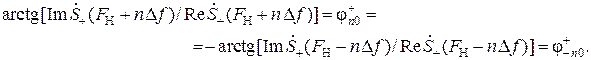
Значит, s_n(t) = s_+n(t) + s_{– n}(t) =

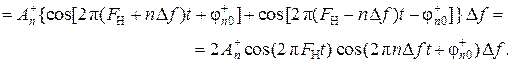
Если просуммировать все элементарные составляющие добавочного сигнала s₊(t), то получим:

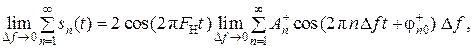
или то есть добавочный сиг-

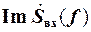
1

0,5

0 F_Н f 0 F_Н f

а)

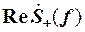
0,5

Δ f nΔ f nΔ f

0 F_Н f 0 F_Н f

б )

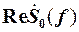
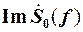
1

 

 

 

0,5