FН f 0 FН f
в)
Рис. 27. Синтез оптимального телеграфного сигнала по Найквисту
сигнал s+(t) представляет собой некоторый амплитудно-модулированный сигнал без несущей и с огибающей 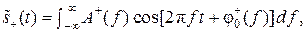 и высокочастотным заполнением cos (2 π FН t).
и высокочастотным заполнением cos (2 π FН t).
Огибающую 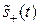 сигнала
сигнала 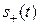 можно выбрать так, чтобы она не имела нулевых переходов вообще. Тогда временнóе положение tl+ нулевых переходов добавочного сигнала s+(t) будет определяться равенством:
можно выбрать так, чтобы она не имела нулевых переходов вообще. Тогда временнóе положение tl+ нулевых переходов добавочного сигнала s+(t) будет определяться равенством:
cos (2 π FН tl+) = 0, или 2 π FН tl+ = (l – 1/2) π, или tl+ = τэ (l – 1/2).
Если во входном элементарном сигнале sвх(t) = A sinc (π t/τэ) ввести задержку на величину tз = τэ /2, то во всех характерных (отсчётных) точках tm = τэ (m + 1/2) сигнала s0(t) = sвх(t – τэ /2) = A sinc [2 π FН(t – τэ /2)] величина cos (2 π FН tm) = cos [2 π FН τэ (m + 1/2)] = cos [π (m + 1/2)] = sin (m π) равна нулю. Значит, построенный нами добавочный сигнал s+(t) в мгновенные значения идеального телеграфного сигнала s0(t) в середине каждого из элементарных временных интервалов длительностью τэ линейных искажений вносить не будет, но зато может «погасить» колебания идеального сигнала s0(t) при t ≤ 0 и сделать его физически реализуемым.
Всё это справедливо для многоуровневой телеграфии, в которой (в подавляющем большинстве случаев) соседние посылки не имеют одинаковых амплитудных множителей ah. В двухуровневой однополярной телеграфии (в обычном телеграфе) это может случаться очень часто. Поэтому в обычном телеграфе следует на интервале длительностью τэ передавать одну из двух элементарных посылок с амплитудами ah = +A либо – A и длительностью τ h = τэ /2. Спектр таких посылок будет равным S(ω) = ± A sinc (ω τэ /4). В пределах полосы пропускания телеграфной линии связи [0, FН = 1/(2 τэ)] будет располагаться лишь часть энергии элементарной посылки. Чтобы наиболее полно использовать линию связи (то есть максимизировать отношение сигнал/помеха на выходе телеграфного канала), следует скорректировать характеристику АЧХ посылки, сделав её прямоугольной в полосе частот [0, FН = 1/(2 τэ)]. А чтобы коэффициент передачи 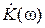 телеграфной линии был физически реализуемым, нужно к нему добавить соответствующий «кососимметричный» член.
телеграфной линии был физически реализуемым, нужно к нему добавить соответствующий «кососимметричный» член.
Такие характеристики телеграфной линии связи могут быть реализованы с помощью хорошо разработанных методов синтеза электрических цепей с минимально-фазовыми коэффициентами передачи. Обычно в качестве физически реализуемого коэффициента передачи такой линии электросвязи используют
функцию «приподнятого косинуса» с коэффициентом скругления α = 0,3 [35]:

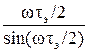 при
при  ;
;
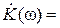
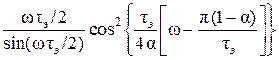 при
при 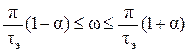 ;
;
0 при  .
.
В Прил. II-В к статье [54] Найквист приводит простой пример реализации телеграфной системы, которая может передавать сообщения со скоростью vт = = 2 FНбез межсимвольных искажений (см. рис. 28.а). При поступлении прямоугольных посылок на вход такой системы на её выходе получаются сигналы (рис. 28.б ), представляющие собой затухающие колебания с эквидистантным расположением своих нулевых переходов (как у функции отсчётов!), что и обеспечивает неискажённую передачу сообщений с предельно возможной скоростью.
Далее Найквист получает аналогичные результаты для многоканального телеграфа с частотным разделением каналов, рассматривает телеграфию с произвольной формой элементарных посылок и эквивалентность (дуальность) временнóго анализа и частотного. Тем самым он полностью решает вопрос о значении коэффициента К в формуле W = K log т:величина К не может превосходить величину 2 FН,но может быть достаточно близкой к ней.
Наконец – он возвращается к оценке возможного числа уровней т,используемых для многоуровневой телеграфии. Найквист приходит к выводу, что число т ограничивается двумя факторами: максимально возможными (в данной телеграфной системе) уровнями токов или напряжений и уровнями электрических помех. Найквист заключает [54]: «Если помеха непредсказуема, её абсолютная величина должна быть меньше, чем половина разности между любыми двумя уровнями тока, используемыми для телеграфирования [курсив наш – Г. Х.]».
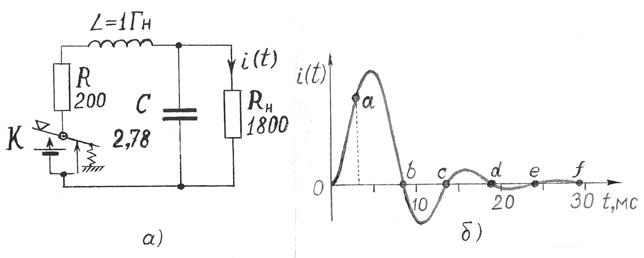 Рис. 28. Реализация (Найквиста) телеграфной системы,
Рис. 28. Реализация (Найквиста) телеграфной системы,
имеющей наибольшую скорость телеграфирования
Отсюда непосредственно следует формула (Найквист почему-то её не приводит): W = 2 FНlog (Iмaкc /Iп+ 1), где W – скорость передачи сообщений (мы бы сказали: информации); FН– частота среза частотной характеристики телеграфного канала; Iмaкc – максимально допустимый ток в телеграфной линии; Iп – максимальный уровень помех в этой линии.
Как видим, роль Г. Найквиста в разработке прикладной теории информации аналогична роли М. Фарадея в разработке электродинамики: К. Шеннону «оставалось только обобщить»результаты Найквиста и провести их строгое математическое обоснование. Хотя содержание статьи Найквиста [54] 1928 г. не имеет прямого отношения к теореме отсчётов, результаты этой статьи являются выдающимися, что по достоинству было оценено лишь в конце 1980-х гг.
Таким образом, фундаментальные результаты Г. Найквиста по оцениванию предельно достижимой скорости телеграфирования могут быть практически реализованы, по крайней мере, в двух простейших вариантах.
Если мы передаём аналоговый сигнал с финитным спектром, ограниченным верхней частотой Fm, то (без учёта электрических помех в линии связи) для его передачи можно использовать аналоговый канал с «кососимметричным» коэффициентом передачи и с частотой среза (Найквиста) FН = Fm. При этом на входе канала передачи «непрерывных сообщений» передаваемый сигнал превращается в ступенчатый сигнал с длительностью «элементарных ступенек» τэ = 1/(2 Fm) и значениями амплитуды этих «ступенек», равными мгновенным значениям передаваемого сигнала в середине каждой «ступеньки».
На выходе канала связи мгновенные значения выходного сигнала в середине соответствующих интервалов времени длительностью τэ будут пропорциональны соответствующим им мгновенным значениям переданного сигнала. Зная этот коэффициент пропорциональности (например, измеряя его текущее значение по эталонной – единичной – посылке), можно восстановить все дискретные отсчёты переданного сигнала и в соответствии с теоремой Котельникова-Шеннона полностью восстановить переданное сообщение.
Если мы хотим передавать некоторое бинарно-закодированное сообщение с помощью обычного телеграфа со скоростью vт, то следует организовать синхронизированную линию электросвязи такого телеграфа с тактовой частотой синхронизации vт = 2 FН и с коэффициентом передачи типа «приподнятого косинуса» с частотой среза FН. Сообщения следует передавать бинарными посылками длительностью τ э = 1/(4 FН), а на приёмном конце телеграфа реализовать синхронную обработку согласно методу Найквиста.
В статьях 1940 и 1948 гг. ([46], с. 433-460 и 243-332) Клод Шеннон завершил создание основ прикладной теории информации, продолжив развитие идей своих старших коллег по БТЛ Г. Найквиста и Р. Хартли. Он впервые ввёл в рассмотрение меру количества информации для неравновероятных сообщений
(энтропию источника ДИС), а также количественную меру для степени потери информации в каналах КПДС при наличии в последних различного рода помех (пятый постулат ПТИ – см. разд. 7).
В разд. 9 мы провели оценивание информационной ёмкости ℰ каналов передачи дискретных сообщений (КПДС), то есть рассмотрели информационную эффективность передачи сообщений по различным каналам КПДС в статическом режиме его работы. Проведённые в разд. 16 рассуждения позволяют достаточно просто обобщить результаты разд. 9 на динамические каналы КПДС, работающие в режиме реального времени в присутствии помех.
Итак, дискретные сообщения из ансамбля 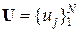 с помощью квантованных уровней
с помощью квантованных уровней  электрического напряжения на входе линии связи мы можем (в отсутствие в канале КПДС помех) без линейных искажений передавать с «физической скоростью» vт = 1/(2 FН), где FН – частота среза линии электросвязи (Найквиста). В этом случае скорость передачи информации vи (при полностью снятой избыточности источника дискретных сообщений) будет определяться выражением: vи = log N/(2 FН).
электрического напряжения на входе линии связи мы можем (в отсутствие в канале КПДС помех) без линейных искажений передавать с «физической скоростью» vт = 1/(2 FН), где FН – частота среза линии электросвязи (Найквиста). В этом случае скорость передачи информации vи (при полностью снятой избыточности источника дискретных сообщений) будет определяться выражением: vи = log N/(2 FН).
Как же повлияют помехи в канале КПДС на величину скорости vи, если «физическую скорость передачи» мы увеличить не можем, поскольку она определяется частотой Найквиста FН?
Пусть в полосе пропускания канала электросвязи присутствует аддитивный белый гауссовский шум (АБГШ) со средней спектральной плотностью мощности N0 и пусть модуль коэффициента передачи канала имеет вид:
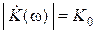 при | ω | ≤ 2 π FН и
при | ω | ≤ 2 π FН и  при | ω | > 2 π FН.
при | ω | > 2 π FН.
Тогда на выходе канала электросвязи корреляционная функция RН(τ) шума АБГШ ξН(t) есть:
RН(τ) = 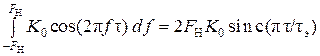 .
.
Значит, при τn = n τэ корреляционная функция RН(τ n) = 0.
Если же мы к прямоугольному коэффициенту передачи 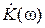 добавим «кососимметричный» член, то получим результирующий коэффицеинт передачи канала связи:
добавим «кососимметричный» член, то получим результирующий коэффицеинт передачи канала связи:

Отсюда:
 или
или
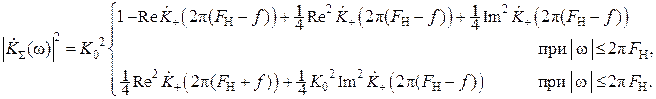
Таким образом, получаем:
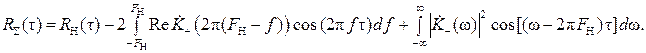
В силу зеркальной симметрии функции 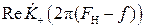 и чётности функции cos (2 π f τ) получаем:
и чётности функции cos (2 π f τ) получаем:
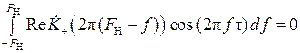 .
.
Корреляционная функция «добавочного» шума R+(τ), в силу чётности функции 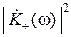 , есть:
, есть:
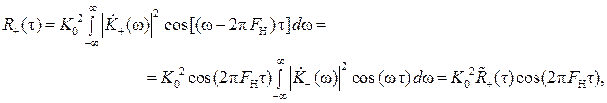
где  – огибающая функции
– огибающая функции 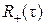 , а FН – частота её высокочастотного заполнения.
, а FН – частота её высокочастотного заполнения.
Значит, стационарные гауссовские шумы на выходе канала электросвязи с коэффициентом передачи 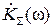 имеют в качестве корреляционной функции
имеют в качестве корреляционной функции
RΣ(τ) функцию: RΣ(τ) = RН(τ) + K02  cos (2 π FН τ).
cos (2 π FН τ).
Корреляционная функция 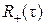 имеет нулевые переходы в точках τ n, удовлетворяющих уравнению: 2 FН τ n = n /2. При FН = 1/(2 Tэ) получаем: τ n = n τэ /2.
имеет нулевые переходы в точках τ n, удовлетворяющих уравнению: 2 FН τ n = n /2. При FН = 1/(2 Tэ) получаем: τ n = n τэ /2.
Значит, корреляционная функция RΣ(τ) шумов ξΣ(t) на выходе канала электросвязи с коэффициентом передачи 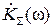 имеет нулевые значения в точках τ n = n τэ /2, то есть мгновенные значения реализаций шума ξΣ(t) в точках t = t1 и t = t2 при t2 – t1 = τэ не коррелированы, а в силу их гауссовости – независимы.
имеет нулевые значения в точках τ n = n τэ /2, то есть мгновенные значения реализаций шума ξΣ(t) в точках t = t1 и t = t2 при t2 – t1 = τэ не коррелированы, а в силу их гауссовости – независимы.
Мы доказали, что
| в динамическом многоуровневом канале передачи дискретных сообщений, имеющем линию электросвязи с шириной полосы пропускания ΔF = 2 FН (по уровню половины модуля коэффициента передачи линии), количества передаваемой по каналу КПДС информации, которое соответствуют дискретным отсчётам, отстоящим друг от друга на интервалы n τэ = n/(2 FН), суммируются. |
В разд. 9 мы рассмотрели информационную ёмкость ℰ(Q) статических каналов КПДС и вывели её асимптотическую оценку – формулу Клода Шеннона: ℰШ(Q) = log 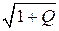 .
.
Поскольку в динамическом канале КПДС в единицу времени мы можем передавать 1/Tэ = 2 FН отсчётов, то при стационарном режиме работы динамического канала КПДС мы можем передавать сообщения с информационной скоростью CШ(Q) = 2 FН ℰШ(Q) = FН log (1 + Q).
Таким образом, мы связали информационную статику с информационной динамикой, теорему Котельникова-Шеннона с интервалом и частотой Найквиста и доказали центральную теорему прикладной теории информации:
| информационная скорость передачи дискретных сообщений (по обычным каналам электросвязи) при наличии в них аддитивных белых гауссовских шумов ограничена сверху пределом CШ(Q) = FН log (1 + Q), где FН – частота среза (Найквиста) линии электросвязи, рассматриваемой как фильтр нижних частот (Гц), Q – отношение сигнал/шум (по мощности), CШ(Q) – информационная пропускная способность аналогового канала передачи дискретных сообщений (бит/с). |
Формулу CШ(Q) = FН log 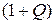 назовём формулой Шеннона информационной динамики.
назовём формулой Шеннона информационной динамики.
Перейдём к рассмотрению так называемых «непрерывных сообщений» и «оптимальных каналов» передачи таких сообщений.
Вопросы для самопроверки
1. Какова простейшая математическая модель динамического источника дискретных сообщений?
2. Что такое производительность динамического источника дискретных сообщений?
3. Какова максимальная производительность бинарного динамического источника дискретных сообщений?
4. Каким образом передаётся дискретная информация в динамической системе передачи информации в отсутствие помех?
5. Как формулируется основная теорема Шеннона информационной динамики для дискретного канала без помех?
6. Как формулируется основная теорема Шеннона информационной динамики для дискретного канала при наличии в канале помех?
Дата добавления: 2015-05-16; просмотров: 1003;
