Передачи информации. Проблема дискретизации сигналов

В динамических каналах передачи дискретных сообщений элементарные сообщения (символы) передаются с помощью различных сигналов, которые представляют собой, например, изменение во времени напряжения в электрических цепях динамического канала КПДС s(t).

В существующей научно-технической литературе имеется большая путаница относительно динамических характеристик каналов передачи сообщений [5, 6, 46]. Обычно «блуждаютв трёх соснах»: формула Э. Уиттекера (1914 г.) математической теории интерполяции функций, интервал (шаг, период) дискретизации Г. Найквиста (1928 г.), фигурирующий в телеграфии при ограниченной полосе пропускания линии электросвязи и теорема (формула) Котельникова(1932 г.)-Шеннона(1940 г.) теории дискретизации сигналов.

Рассмотрим так называемые «кардинальные функции» Уиттекера и их полезные для дальнейшего применения свойства.

В результате решения «чистыми математиками» математической проблемы интерполяции функций были получены интерполяционные формулы Ньютона, Стирлинга, Лагранжа, Гаусса, Бесселя, Эверетта, Стеффенсена и др. О. Коши в 1841 г. и Э. Борель в 1897 г. рассматривали интерполяционные ряды

вида:

f (t) = 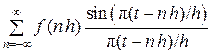. (16.1)

Однако первым, кто осознал важность представления (16.1) для прикладной математики и провёл достаточно подробные исследования свойств ряда (16.1), был шотландский математик Эдмунд Уиттекер [39] (не путать с его старшим сыном Джоном, который также занимался проблемами интерполяции). Э. Уиттекер показал (см. [39, 58]), что если некоторая неизвестная функция f (t) задана своими эквидистантными отсчётами { f_n = f (a + n Δt)} в бесконечной совокупности точек (…, a – Δt, a, a + Δt, a + 2 Δt, …), то среди бесконечного множества функций, которые можно провести через совокупность отсчётов (…, f_–1, f₀, f₁, f₂, …), существует одна-единственная функция, не имеющая разрывов второго рода (сингулярностей) и быстрых осцилляций между отсчётными точками. Такую функцию C(t) Э. Уиттекер назвал основной, или кардинальной функцией (cardinal function) для системы { f (a + n Δt)} :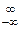

C(t) = 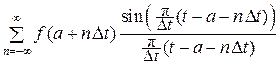= 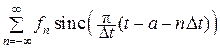, (16.2)

где sinc (x) ≡ (sin x)/x, а величина Δt называется интервалом дискретизации.

Например, если a = 0 и f_n = (–1)ⁿ, то

C(t) = 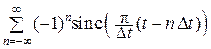= 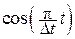. (16.3)

При этом формулу (16.3) нельзя рассматривать как применение теоремы отсчётов Котельникова-Шеннона к функции cos (2 π F t) при F = 1/(2 Δt), поско-льку при a = Δt /2: f_n = cos [π (a + n Δt)/Δt] = cos [π (n + 1/2)] = 0 для любого значения n, и ряд (16.2) тождественно равен нулю.

В заключение своей статьи 1914 года [58] Э. Уиттекер написал:

«В последнее время прикладные математики жалуются на то, что Чистая Математика ежедневно становится всё более сложной и трудной для понимания. Особенно это относится к повышенной строгости, с которой в настоящее время излагаются теоремы Математического Анализа и которая тесно связана с введением в рассмотрение разрывов, сингулярностей и других явлений, не рассматривавшихся в классической математике. Действительно, современная Теория Функций Действительной Переменной широко занимается рассмотрением случаев, в которых наличие флуктуаций и сингулярностей превосходят все границы интуитивных или геометрических представлений. Кажется возможным, что некоторых из таких затруднений можно избежать введением функции, аналогичной “кардинальной функции” данной работы, которая была бы более простой, чем рассматриваемая функция, но была бы равной ей в бесконечном числе значений переменной и могла бы заменить её во всех практических и некоторых теоретических исследованиях» [выделения и курсив Уиттекера – Г. Х.].

Дальнейшие свойства кардинальных функций исследовал в 1925-27 гг. ученик Уиттекера – У. Феррер [39]. Он обнаружил у кардинальных функций замечательное свойство «самосогласованности» (соответствующий термин “consistency” у Феррера взят в кавычки и требует неформального перевода на русский язык).

Теорема Феррера: 1927 г. [39]). Если , то

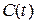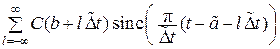= , (16.4)

где 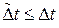, b – произвольное число. То есть для самосогласованности (иначе говоря – однозначной определённости) кардинальной функции C(t) достаточно, чтобы отсчёты { f_n} 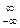соответствующим образом убывали на бесконечности.

Однако из расходимости ряда 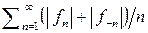не следует отсутствие самосогласованности функции 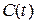, соответствующей ряду (…, f_–1, f₀, f₁, f₂, …). Тем не менее, разложение (16.3) для функции cos (π t/Δt) свойством однозначной определённости (самосогласованности) не обладает, то есть

cos (π t/Δt) 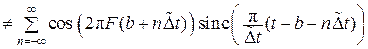. (16.5)

Как видим, кардинальные функции C(t) имеют к проблеме дискретизации косвенное отношение.

После сделанных замечаний можно обратиться к проблеме дискретизации сигналов. Докажем теорему Котельникова-Шеннона.

Теорема Котельникова-Шеннона. Пусть сигнал s(t) как функция времени t (– ∞ < t < ∞) обладает конечной энергией и ограниченным по частоте (финитным) спектром: 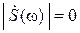при | ω | > 2π F_m.

Тогда сигнал s(t) может быть представлен в виде ряда Уиттекера:

, (16.6)

где sinc (x) = (sin x)/x – так называемая «функция отсчётов»;

s_n = s(a + nΔt) – отсчёт функции s(t) в точке t = a + n Δt;

a – произвольное действительное число, и ряд (16.1) в каждой точке t будет сходиться среднеквадратически, если частота дискретизации F_д = 1/Δt будет не менее значения 2 F_m, то есть если выполняется неравенство: F_д ≥ 2 F_m.

При этом 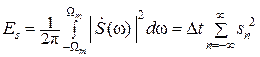, где Ω_m ≡ 2 π F_m, Δt ≤ 1/(2F_m).

Вид функции отсчётов 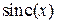= 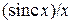, где x = π t/Δt, представлен на рис. 25.

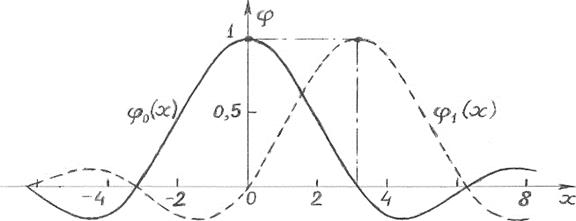
Рис. 25. Вид функций отсчётов φ₀(x) = sinc(x) и φ₁(x) = sinc(x – π)

Доказательство. Поскольку E_s < ∞, то есть сигнал s(t) принадлежит действительному гильбертову пространству L₂(t), то он имеет преобразование Фурье (спектральную плотность, или спектр)

.

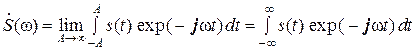При этом .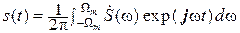

В силу финитности спектра 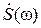его можно периодически продолжить вне интервала круговых частот 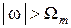с некоторым периодом 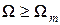и пред-

ставить формальным рядом Фурье:

,

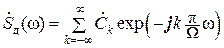где .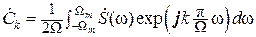

А поскольку Ω ≥ Ω _m, то

,

.

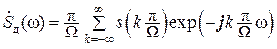Чтобы спектр сигнала s(t) оставался прежним, функцию 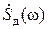следует умножить на функцию Π(Ω, ω):

Π(Ω, ω) = 1 при | ω | ≤ Ω и Π(Ω, ω) = 0 при | ω | > Ω.

Поэтому .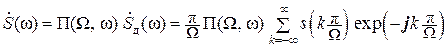

Значит,

=

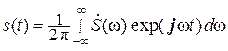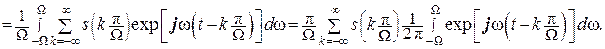
В результате получаем разложение:

.

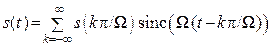Введём обозначение: Δt = π /Ω = 1/(2F_д). Тогда окончательно имеем

.

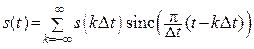При этом (по построению)

,

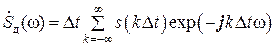где F ≥ F_m, или Δt ≤1/(2 F_m), или F_д≥2 F_m.

Сдвиг начала оси времени на величину a ничего принципиально нового в проведённое доказательство не вносит, так как он сводится к добавлению в фазочастотную характеристику сигнала линейного слагаемого вида φ(ω) = a ω.

Непосредственным вычислением можно проверить, что

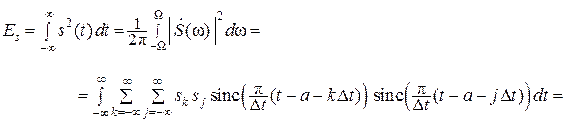
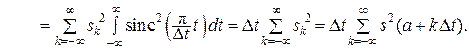
Подчеркнём, что обратная теорема не справедлива: если некоторая функция f (t) представлена в виде ряда (16.6), то она может вовсе не иметь преобразования Фурье. В этом мы убедимся ниже.

Значит, финитность спектра функции f (t) является условием достаточным для возможности однозначного представления функции в виде ряда Уиттекера (16.6), но не необходимым.

Поскольку отсчёты сигналов с ограниченной энергией удовлетворяют условиям самосогласованности (теорема Феррера), то справедливо равенство:

=

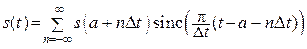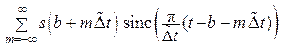
при произвольном b ≠ a; при этом .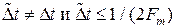

Разложение (16.6) называется теоремой отсчётов для детерминированных сигналов с финитным спектром и ограниченной энергией.

Сигналы с ограниченной энергией и финитным спектром принадлежат к одному из частных видов так называемых гильбертовых функциональных пространств с воспроизводящим ядром (ГПВЯ). Таких подпространств существует несколько. Например [37], если множество функций из L₂(t), определённых только при 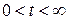, и таких, что финитно их синус-преобразование Фурье (скажем, амплитуда волн точечного гармонического источника звука в бесконечном воздушном пространстве), то есть

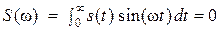при | ω | > 2π F_m,

и при этом 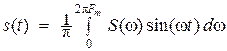, то воспроизводящее ядро этого функционального пространства ГПВЯ 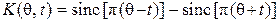, а любая

функция s (t) из этого пространства разлагается в ряд (см. рис. 26.а):

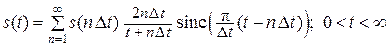. (16.7)

Если функция f (t) 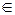L₂(t) имеет финитное косинус-преобразование Фурье (например, амплитуда колебаний полубесконечной упругой струны, начало которой прикреплено к гармоническому вибратору), то функцию f(t) можно представить в виде (см. рис. 25.б ):

. (16.8)

Обратим внимание на то, что в разложениях (16.7), (16.8) величина a = 0.

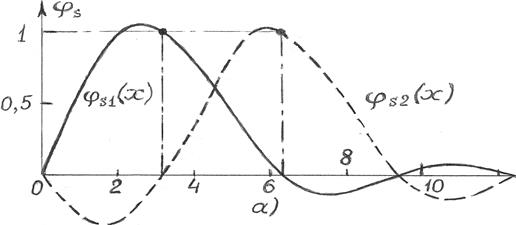
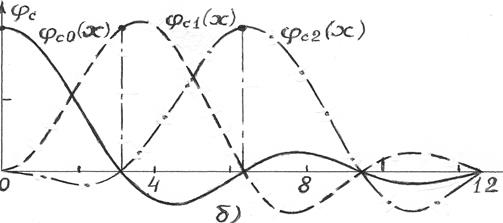
Рис. 26. Вид функций отсчётов: а) φ_s(x) и б ) φ_c(x)

Как уже отмечалось (см. разд. 2), разложение (16.6) при a = 0 в теорию сигналов впервые ввёл в 1933 г. В. А. Котельников, который на основании этого разложения доказал ряд практически важных теорем – в том числе и теорему отсчётов. Чуть ранее (в 1928 г.) буквально «прошли мимо» этой теоремы выдающиеся радиотехники Г. Найквист – в статье [54] и К. Купфмюллер [51]. При построении прикладной теории информации К. Шеннон в 1940 г. «переоткрыл» теорему отсчётов ([46], с. 435), а в 1948 г. он привёл пример модели «белого шума» с ограниченной полосой частот ([46], с. 292). И хотя К. Шеннон не обобщил теорему отсчётов на стационарные случайные процессы с финитной спектральной плотностью мощности, в своих теоретических построениях он, «по умолчанию», использовал это обобщение.

Поэтому теорему отсчётов теории сигналов следует называть теоремой Котельникова-Шеннона. А учитывая достижения в этой области науки сэра Уиттекера и Г. Найквиста, в приведённой выше теореме отсчётов следует называть представление (16.6) – рядом Э. Уиттекера (при a ≠ 0), а максимально возможный интервал дискретизации Δt_макс = 1/(2 F_m) (по предложению К. Шеннона: [46], с. 437) – интервалом Г. Найквиста.

Обобщим теорему отсчётов Котельникова-Шеннона на стационарные случайные процессы.

Известно [8], что всякий стационарный случайный процесс ζ(t) может быть представлен, и притом единственным образом, суммой (разложением Вольда): ζ(t) = η(t) + ξ(t), где η(t) – сингулярный случайный процесс, ξ(t) – регулярный случайный процесс; при этом процессы η(t) и ξ(t) не коррелированы между собой (в случае гауссовости процесса ζ(t) – и независимы).

Обобщённая спектральная плотность средней мощности W_η(ω) (энергетический спектр) сингулярного процесса η(t) имеет вид: W_η(ω) = 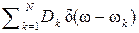, где {ω₁, ω₂, …, ω_k, …, ω_N}, то есть у сингулярных процессов энергетический спектр – линейчатый, а его реализации представляют собой почти периодические функции (Бора) с независимыми случайными коэффициентами η _k, имеющими дисперсию D_k. Как показано выше, такие процессы не могут быть однозначно представлены в виде ряда Уиттекера.

Регулярные стационарные процессы ξ(t) имеют кусочно-непрерывную спектральную плотность мощности W_ξ(ω) и являются реакциями некоторого стационарного линейного (не обязательно физически реализуемого!) фильтра с коэффициентом передачи 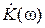на «белый шум», то есть на стационарный случайный процесс с корреляционной функцией вида: R_б.ш.(τ) = N₀ δ(τ), где N₀ – спектральная плотность мощности белого шума (W_б.ш.(ω) = N₀).

Это следует из того, что функция W_ξ(ω) – неотрицательная, а действие

фильтра с коэффициентом передачи 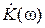на спектральную плотность мощности W_вх(ω) входного случайного процесса имеет вид^ W_вых(ω) = W_вх(ω) | 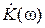|². Отсюда W_ξ(ω) = N₀ | 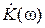|², где 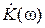– амплитудно-частотная характеристика формирующего данный регулярный случайный процесс ξ(t) фильтра.

Если мощность P_ξ процесса ξ(t) не ограничена, то есть если P_ξ = = 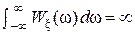, то его дисперсия D_ξ = 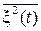= R_ξ(0) = P_ξ = 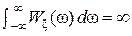, и процесс ξ(t) не может быть представлен рядом Уиттекера, поскольку отсчёты

ξ _n = ξ(a + n Δ t) в этом случае не могут быть определены (будут иметь «бесконечные значения»).

Если P_ξ < ∞, то процесс ξ(t) может быть представлен совокупностью реализаций {ξ_i(t)} 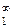, которые являются гармониками вида ξ(t) = α cos (ωt + φ), где α, φ, ω – независимые случайные величины; при этом величина α – распределена по закону Релея со среднеквадратическим значением s_α = 1, φ – равномерно на промежутке (– π, π], ω – с плотностью вероятности p(ω) = W_ξ(ω)/P_ξ. Реализации таких не-эргодических процессов, так же как и сингулярных процессов η(t), не могут быть представлены в виде ряда Уиттекера.

Таким образом, мы исключили из множества стационарных случайных процессов {ζ(t)} те подмножества, реализации которых не могут быть однозначно представлены рядами Уиттекера со случайными коэффициентами, поскольку не обладают свойством самосогласованности Феррера (16.4): сингулярные стационарные процессы, стационарные процессы с бесконечной мощностью и не-эргодические процессы.

Теорема отсчётов для гауссовских регулярных стационарных случайных сигналов.Для определённости мы ограничимся рассмотрением множества стационарных случайных сигналов {ξ(t)}, мгновенные значения которых ξ = ξ(t) распределены по закону Гаусса. Обобщение на негауссовские регулярные случайные сигналы принципиальных затруднений представлять не должно, а гауссовские сигналы для радиотехнических систем представляют наибольший пра-ктический интерес. Кроме того, будем полагать, что среднее значение 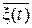= 0, где черта сверху является символом усреднения по ансамблю реализаций {ξ_i(t)} 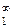случайного сигнала ξ(t).

Теорема. Если стационарный регулярный гауссовский случайный сигнал ξ(t) с ограниченной мощностью (P_ξ = 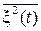< ∞) является эргодическим и имеет финитную спектральную плотность средней мощности (энергетический спектр) W_ξ(ω) = 0 при | ω | > 2π F_m, то его реализации могут быть однозначно представлены в виде:

ξ(t) = 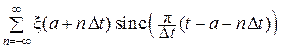, (16.9)

а корреляционная функция 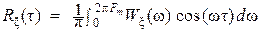такого сигнала ξ(t):

R_ξ(τ) = 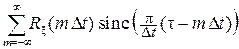, (16.10)

где a – произвольное число и величина Δt ≤ 1/(2 F_m).

Обратим внимание на то, что в разложении для 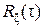: a = 0.

Доказательство. Из курса «Статистическая теория радиотехнических систем» (см., например, [42]) известно, что реализации белого шума могут быть представлены в форме пуассоновского потока дельта-импульсов с гауссовскими случайными коэффициентами. Следовательно, реализации гауссовского регулярного стационарного случайного процесса ξ(t) можно представить в виде

ξ(t) = 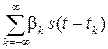, (16.11)

где β_k – независимые гауссовские случайные величины с нулевыми средними 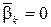и с одинаковыми дисперсиями σ_k² = D_β;

{t_k} 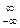– пуассоновская совокупность моментов времени t_k с интенсивностью λ;

s(t) – формирующий сигнал: s(t) = .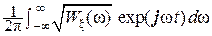

При этом λ D_β = 1, а мощность P_ξ процесса ξ(t) численно равна величине энергии сигнала s(t): P_ξ = λ D_β E_s = E_s.

Ясно, что представление (16.11) является эргодическим, поскольку по одной из реализаций (16.11) процесса ξ(t) может быть определена спектральная

плотность формирующего сигнала s(t), а также величины λ и D_β, а значит и спе-

ктральная плотность мощности W_ξ(ω) = λ D_β | |².

По теореме Парсеваля 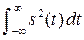= = 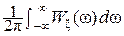P_ξ < ∞.

Значит, формирующий сигнал s(t) имеет ограниченную энергию: E_s = P_ξ.

Если спектральная плотность мощности W_ξ(ω) – финитна, то

= ,

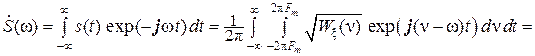
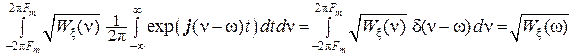то есть формирующий сигнал s(t) также имеет финитный спектр ( 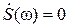при | ω | > 2 π F_m), и к сигналу s(t) может быть применена теорема Котельникова-Шен-

нона:

s(t) = 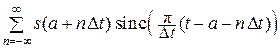. (16.12)

Подставляя разложение (16.12) в формулу (16.11), получаем

ξ(t) = 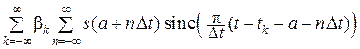. (16.13)

Поскольку ряд Уиттекера (16.12) для функции s(t) обладает свойством самосогласованности, то равенство (16.13) не нарушится, если при каждом зна-

чении k положить a = b – t_k. Тогда

ξ(t) = .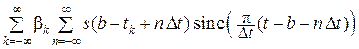

Поменяем порядок суммирования по k и по n:

ξ(t) = 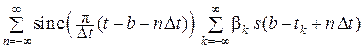. (16.14)

Сравнивая выражения (16.14) и (16.11), видим, что

ξ(t) = .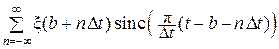

Для корреляционной функции R_ξ(τ) получим разложение:

R_ξ(τ) =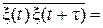

= =

=

= .

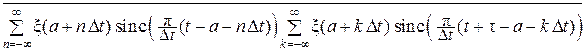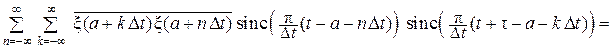
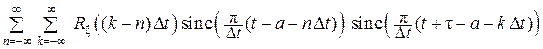Положим a = t; тогда:

,

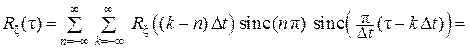
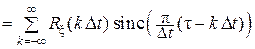поскольку sinc (0) = 1, а при n ≠ 0 значение sinc (n π) = 0.

Теорема доказана.

Обратим внимание на то, что в разложении (16.9) для реализаций случайного сигнала ξ(t) величина a – произвольная, а в разложении (16.10) для корреляционной функции a = 0. Кроме того, несмотря на то, что реализации сигнала ξ(t) не удовлетворяют условиям теоремы Феррера, они допускают однозначно определённое представление (16.9).

Практический смысл условия эргодичности стационарного случайного сигнала ξ(t) в доказанной выше теореме такой же, как условия принадлежности детерминированного сигнала s(t) пространству L₂(t) в теореме Котельникова-Шеннона: отсутствие в сигнале s(t) или в реализациях сигнала ξ(t) сингулярных составляющих вида A cos (ω t + φ).

Таким образом, мы имеем чисто математическую сторону этих двух взаимно дополнительных теорем отсчётов и «физическую» (прикладную) сторону, связанную с их практическим применением: отсчёты низкочастотного («видео-») сигнала s(t) или ξ(t) с финитными спектрами 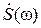или W_ξ(ω), для их точного воспроизведения с помощью ряда Э. Уиттекера, следует брать с частотой дискретизации F_д не меньшей, чем двусторонняя (полная) ширина полосы частот [–F_m ≤ f ≤ F_m], занимаемая этим сигналом: .

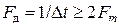Аналогичные теоремы отсчётов существуют и для узкополосных высокочастотных сигналов (радиосигналов).

На примере случайного процесса ζ(t) мы убедились, что реализации некоторых нестационарных случайных процессов могут быть представлены в виде разложения (16.6), то есть существуют теоремы отсчётов и для нестационарных процессов, а также и при неэквидистантных отсчётных моментах времени.

Ещё раз подчеркнём следующее. Ряд Э. Уиттекера (16.2) однозначно определяет кардинальную функцию C(t) для бесконечной серии эквидистантных отсчётов (…, f (a – Δt), f (a), f (a + Δt), f (a + 2 Δt), …) некоторой неизвестной нам функции f (t) и служит для интерполяции этой функции в промежутках между её отсчётами. При этом оказывается, что спектр Фурье функции C(t) вне интервала круговых частот [– 2 π /Δt ≤ ω ≤ 2 π /Δt] – нулевой, а спектр функции f(t) нам вообще говоря – неизвестен.

Представление (16.9) для регулярных гауссовских стационарных случайных сигналов ξ(t), имеющих финитный энергетический спектр (W_ξ(ω) = 0 при | ω | > 2 π F_m), является однозначным при условии, что сигнал ξ(t) является эргодическим, а величина интервала дискретизации Δt меньше или, в крайнем случае, равна величине 1/2 F_m. Представление (16.9) служит для технически грамотного конструирования аналогово-цифровых преобразователей в современных компьютеризованных электронных системах и системах обработки непрерывных сигналов. Ясно, что импульсная цифровая последовательность, соответствующая данному аналоговому сигналу, имеет спектр, ширина которого намного превышает ширину спектра исходного сигнала.

Вместе с тем, информационная пропускная способность каналов электросвязи определяется шириной полосы пропускания канала и уровнем помех, имеющихся в данной системе передачи дискретных сообщений. Этот вопрос мы рассмотрим в разд. 16, являющемся центральным в прикладной теории информации.

Вопросы для самопроверки

1. Каким образом приближённо вычисляется количество информации на выходе канала электросвязи при произвольном распределении сигналов и произвольных аддитивных помехах в канале электросвязи?

2. Каким образом выводится центральная формула Шеннона информационной статики?

3. Для каких каналов электросвязи и в каких пределах изменения величины отношения сигнал/шум справедлива центральная формула Шеннона информационной статики?