Цифровых каналов электросвязи
Развитие современных систем сухопутной подвижной радиосвязи (СПРС) массового гражданского применения, наряду с компьютерной техникой, является основной составной частью третьей промышленной революции – информационной. Завершение информационной революции связано с созданием международной цифровой телекоммуникационной системы IMT 2000 (International Mobile Telecommunication system), которая объединит в единую сверхсистему все виды обмена информацией: цифровое телевидение и радиовещание, цифровую телефонную и телеграфную связь, системы передачи данных, территориальные системы стационарной и подвижной радиосвязи и т. п.
Развитие современных систем СПРС можно подразделить на несколько этапов.
Системы СПРСI поколения (1981-1991 гг.) – аналоговые магистральные (транкинговые) и сотовые территориальные системы связи (ТСС) стандартов “SmartTrunk”, MPT 1327, LTR, AMPS, NMT 450 и др. Эти системы использовали стандартную рабочую полосу радиочастот шириной Δ f = 25 кГц (в США – 30 кГц) и частотную модуляцию с малым индексом. Пропускная способность таких систем ограничивается формулой К. Шеннона:
CШ(Q) = Δ f log  .
.
Системы СПРС II поколения (1991-2000 гг.) – цифровые системы подвижной радиосвязи стандартов TETRA, D-AMPS (IS 136), GSM 900 и т. п.
Системы СПРСIII поколения (1991-2010 гг.) – цифровые системы ТСС стандартов EDGE, WCDMA, CDMA 2000-3x.
В настоящее время разрабатываются стандарты для систем СПРСIV поколения.
Основные характеристики цифровых систем СПРС приведены в табл. 2.
Как следует из данных табл. 2, если в современных системах СПРС в основном используется многопозиционная фазовая манипуляция (N-PSK – Phase Shift Keying), то в перспективных радиосистемах связи будет использоваться преимущественно многопозиционная квадратурная амплитудная модуляция (N-QAM – Quadrature Amplitude Modulation).
В системах радиосвязи других видов (силовых ведомств, авиации и т. п.) будут использоваться такие виды цифровой модуляции, как 16-PSK, 32-PSK, 128-QAM, 256-QAM и т. п.
Таблица 2
Основные технические характеристики цифровых систем СПР
| Поко- ление | Стандарт или спецификация | Рабочая полоса частот, МГц | Модуляция | Теоретическая скорость передачи данных, Мбит/с |
| 2G | TETRA | 0,025 | 4-PSK | 0,029 |
| GSM 900 | 0,2 | GMSK | 0,171 | |
| 3G | EDGE | 0,2 | 8-PSK | 0,474 |
| WCDMA | 5,0 | 4-PSK | 0,192 | |
| CDMA 2000-3x | 3,75 | 4-PSK | 3,69 | |
| 4G | HPSA+ | 5,0 | 16-, 32-, 64-QAM | 21,0 |
| LTE | 20,0 | 4-PSK 16-,64-QAM | 100,0 |
В цифровых системах СПРС задающий генератор передатчика вырабатывает два синхронных колебания, начальные фазы которых сдвинуты друг относительно друга на 90º. Одно из них называется косинусным колебанием: sc(t) = = cos (2 π f0 t), а другое – синусным: ss(t) = sin (2 π f0 t), где f0 – частота несущей (у сотовых систем стандарта GSM 900: f0 ≈ 900 МГц, у систем III и IV поколений f0 ≈ 2000 МГц).
На модулятор передатчика поступают эти колебания, а также элементарные посылки длительностью τэ положительной (“единица”) и отрицательной (“ноль”) полярностей (скажем, в радиосистемах стандарта WCDMA τэ = 261 нс).
Если используется простая четырёхпозиционная фазовая манипуляция (4-PSK ) или четырёхпозиционная квадратурная амплитудная модуляция (4-QAM ), которые являются эквивалентными, то входящий информационный поток (… 100111010011000101 …) подразделяется на пары (00), (01), (10) и (11). Косинусная составляющая умножается на первый символом (если “1”, то s1(t) = sc(t)/  ; если “0”, то s1(t) = – sc(t)/
; если “0”, то s1(t) = – sc(t)/  ), а синусная – вторым (если “1”, то s2(t) = ss(t)/
), а синусная – вторым (если “1”, то s2(t) = ss(t)/  ; если “0”, то s2(t) = – ss(t)/
; если “0”, то s2(t) = – ss(t)/  ). Затем поток модулированных таким образом элементарных посылок суммируется и – после усиления по мощности – излучается.
). Затем поток модулированных таким образом элементарных посылок суммируется и – после усиления по мощности – излучается.
Таким вот образом получается высокочастотная элементарная посылка: sΣ(t) = s1(t) + s2(t) = ± sc(t)/  ± ss(t)/
± ss(t)/  .
.
В общем случае элементарный радиосигнал smn(t) с цифровой модуляцией принято записывать в виде:
smn(t) = I(t) cos (2 π f0 t) + Q(t) sin (2 π f0 t)
где I(t) – синфазный (in-phase), Q(t) – квадратурный (quadrature) модулирующий сигналы, которые, в свою очередь, представляются как: I(t) = Im rect(t/τ э), Q(t) = Qn rect(t/τ э), где rect(t/τ э) – прямоугольный импульс длительностью τ э с единичной амплитудой, Im и Qn – амплитуды синфазного и квадратурного компонентов цифрового радиосигнала smn(t). Чтобы сохранить единство терминологии в настоящем пособии, мы будем интерпретировать величину Im как амплитуду косинусной составляющей радиосигнала и обозначать её через Uc, а Qn – как амплитуду синусной составляющей и обозначать её через Us. В то же время, в «классической радиотехнике» синфазным компонентом считается колебание s0(t) = A sin (2 π f0 t). Это следует всегда помнить.
На рис. 30 условно показаны возможные варианты векторного сложения сигналов s1(t) и s2(t): позиции амплитуды суммарного высокочастотного сигнала 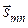 (совокупность позиций
(совокупность позиций 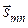 называется сигнальным созвездием). Это аналогично записи комплексной амплитуды
называется сигнальным созвездием). Это аналогично записи комплексной амплитуды  гармонического колебания бесконечной длительности s(t) = |
гармонического колебания бесконечной длительности s(t) = |  | cos (2 π f0 t + arg
| cos (2 π f0 t + arg  ) на плоскости (Re
) на плоскости (Re  , Im
, Im  ).
).
Если используется фазовая манипуляция 8-PSK (см. рис. 30.в), то информационный поток подразделяется на тройки (000), (001), …, (111) и синтезируются элементарные высокочастотные посылки в соответствии с сигнальным созвездием, изображённым на рис. 30.в.

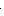
















 Us ≡ Q Us ≡ Q
Us ≡ Q Us ≡ Q







 1
1



















 | |||||||
 |  |  | |||||



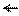


 – 1 0 1 Uc ≡ I
– 1 0 1 Uc ≡ I




 u
u
 – 2 2 Uc ≡ I
– 2 2 Uc ≡ I



 – 1
– 1











 а)
а)










б )
 |  |






 Us ≡ Q 1 Us ≡ Q
Us ≡ Q 1 Us ≡ Q









 2
2











 – 1 1 Uc ≡ I
– 1 1 Uc ≡ I







































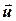







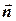

 – 2 2 Uc ≡ I – 1
– 2 2 Uc ≡ I – 1




 в)
в)
 |  |  |
– 2
г)
Рис. 30. Типовые конфигурации сигнальных созвездий
многоуровневых цифровых радиосигналов: а) 4-PSK ≡ 4-QAM;
б ) 16-QAM; в) 18-HAM; г) 8-PSK.
Если используется квадратурная амплитудная модуляция (например модуляция 16-QAM – см. рис. 30.б ), то сигнальное созвездие лежит не на единичной окружности, как при фазовой манипуляции, а в узлах квадратной решётки. Если углы такой решётки исключить, то можно получить более энергоэкономичную модуляцию (например модуляцию 32-QAM ).
Более перспективной для будущих систем СПРС пятого поколения является модуляция N-QAM с гексагональным созвездием (N-HAM – Hexagonal Amplitude Modulation), сигнальное созвездие которой, для случая 18-позицион-ной N-HAM, показано на рис. 30.г. Преимущества модуляции N-HAM перед обычной N-QAM очевидны: более экономно используется общая энергия сигнала; однако модуляция и демодуляция сигналов с гексагональной амплитудной модуляцией несколько сложнее, чем сигналов с обычной модуляцией N-QAM. В том числе, это следует из правил принятия решения в цифровом демодуляторе (см. заштрихованные области на рис. 30). Для случая, например, модуляции 4-QAM правило демодуляции сводится к анализу сочетания знаков косинусной и синусной составляющих результатов синхронного детектирования высокочастотного сигнала. В случае фазовой манипуляции N-PSK анализируется отношение косинусной и синусной составляющих [то есть arctg (Qn/Im)]. В случае многопозиционной модуляции N-QAM (N > 4) – к анализу знаков добавляется анализ относительных величин амплитуд косинусной и синусной составляющих. В случае модуляции N-HAM (N = 6, 18, 36, 60, 90, 126 и т. д.) для принятия решения при демодуляции сигналов следует вычислить величины
(u cos φ0 – Im)2 + (u sin φ0 – Qn)2,
где φ0 – начальная фаза колебаний принятой высокочастотной посылки u(t) = = s(t) + n(t), для всех позиций (m, n) сигнального созвездия, и выбрать наименьшую из них. На рис. 30.г,для примера, штриховкой показаны области принятия положительного решения в случае модуляции 18-HAM.
Далее. При приёме многопозиционных радиосигналов возникают различные искажения сигналов, вызванные как внешними радиопомехами, так и тепловыми шумами входных цепей радиоприёмника, погрешностями синхронизации по частоте и по фазе несущей, нестабильностью задающих генераторов передатчика и приёмника и т. п. В простейшем случае все эти искажения принятых высокочастотных сигналов можно представить аддитивным высокочастотным гауссовским стационарным процессом n(t), так что принятый высокочастотный сигнал можно записать в виде: u(t) = sm n(t) + n(t), а ситуацию при демодуляции принятых сигналов можно описать в виде вектора 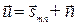 (см. рис. 30), где
(см. рис. 30), где 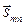 – одна из позиций сигнального созвездия;
– одна из позиций сигнального созвездия; 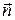 – случайный вектор, имеющий гауссовское распределение на плоскости {I ≡ Uc ≡ x; Q ≡ Us ≡ y} с плотно-
– случайный вектор, имеющий гауссовское распределение на плоскости {I ≡ Uc ≡ x; Q ≡ Us ≡ y} с плотно-
стью вероятности вида:
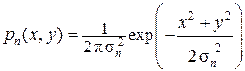 .
.
На рис. 30.а-г функция pn(x, y) представлена парой сечений, изображённых двумя концентрическими кругами радиусов 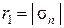 и
и 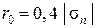 .
.
Для вычисления элементов переходной матрицы П = {Pj k; j, k = 1, 2, …, N } цифровой системы радиосвязи с многопозиционными сигналами следует (обычно численными способами в пакете прикладных программ MathCad, MathLab и т. п.) проинтегрировать плотность вероятности pn(x, y) по соответствующим областям принятия решений при демодуляции сигналов с центрированием функции pn(x, y) в точках сигнального созвездия (Im, Qn).
Например, при модуляции 4-QAM переходная матрица П имеет вид:
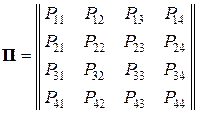 ,
,
где P11 = P22 = P33 = P44 = 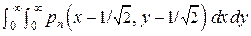 ;
;
P12 = P23 = P34 = P21 = P32 = P43 = P14 = P41 = 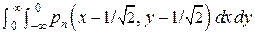 ;
;
P13 = P24 = P31 = P42 =  .
.
Вычислив элементы матрицы П скорость передачи информации можно вычислить с использованием формулы (7.4) или (8.2). Методика таких вычислений представлена в разд. 9.
Однако прежде чем переходить к конкретным примерам вычисления скорости передачи информации и пропускной способности современных цифровых каналов радиосвязи, выведем асимптотическую оценку пропускной способности каналов радиосвязи с многопозиционной цифровой модуляцией.
Согласно негэнтропийной методике Шеннона (см. разд. 12) можно получить асимптотические оценки функции Cц(Q) при бесконечном количестве позиций (N → ∞) сигнального созвездия на плоскости {Uc, Us} (индекс “ц” означает – «цифровая»).
Итак, пусть на плоскости {Uc, Us} совокупность передаваемых по каналу электросвязи сигналов изображается точками (Uc ≡ x, Us ≡ y), имеющими гаусс-
совскую плотность вероятности:
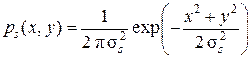 ,
,
где x = I, y = Q.
В таком случае дифференциальная энтропия источника сообщений (сиг-
налов 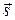 ) есть:
) есть:
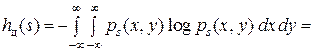

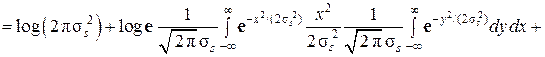
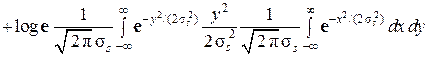 ,
,
или 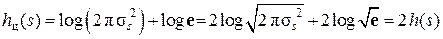 ,
,
где h(s) – дифференциальная энтропия «одномерного сигнала» (см. разд. 11).
Соответственно дифференциальная энтропия «двумерного» (векторного) шума 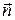 есть: hц(n) = 2 log
есть: hц(n) = 2 log 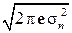 = 2 h(n).
= 2 h(n).
Значит, в двумерном случае:
ℰц(Δu, σs, σn) = hц(s + n) – hц(n) = 2 [h(s + n) – h(n)],
или ℰц(Δu, σs, σn) = 2 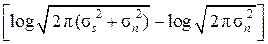 =
= 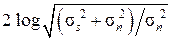 ,
,
или ℰц(Δu, σs, σn) = 2 ℰ(Δu, σs, σn) = 2  ,
,
где ℰ(Δu, σs, σn) – информационная ёмкость статического аналогового канала передачи КПДС с «одномерными сигналами» с бесконечным количеством уровней при (одномерном) гауссовском их распределении;
ℰц(Q) – информационная ёмкость статического канала КПДС с бесконечным числом позиций сигнального созвездия на плоскости {I, Q} при их круговом двумерном гауссовском распределении.
Как видим, для современных цифровых каналов КПДС с многопозиционными сигналами информационная пропускная способность канала КПДС определяется «двумерной динамической формулой Шеннона»:
Cц(Q) = 2 FН ℰ(Q) = 2 FН 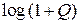 = 2 C(Q).
= 2 C(Q).
Это объясняется тем, что в цифровых системах радиосвязи в качестве переносчиков сообщений можно использовать как амплитуды элементарных радиопосылок, так и начальные фазы несущей радиосигналов.
В аналоговых телефонных системах (без использования тональной или надтональной модуляции), а также в многоуровневых телеграфных каналах электросвязи такая возможность отсутствует. Однако в аналоговых радиосистемах такая возможность появляется, а потому в радиосистемах, исполь-зующих амплитудную модуляцию с одной боковой полосой радиочастот, пропускная способность, по сравнению с классическими телефонными и телеграфными системами электросвязи, почти удваивается.
Перейдём к рассмотрению информационных ёмкостей и пропускных способностей каналов КПДС с некоторыми конкретными цифровыми методами модуляции.
В разд. 12 ( рис. 16) мы рассматривали простейший пример многоуровневого телеграфа с идеализированными равномерно распределёнными помехами в канале электросвязи. Поскольку источник ДИС без информационной избыточности (то есть у источника ДИС все априорные вероятности знаков на входе канала КПДС равны между собой: Pj = 1/N ) согласован с таким каналам КПДС,
то мы получили информационную ёмкость такой системы передачи ℰ =
=  , где Q – отношение сигнал/помеха, то есть при Q >> 1 величина
, где Q – отношение сигнал/помеха, то есть при Q >> 1 величина
информационной ёмкости ℰ такая же, какую даёт статическая система передачи
информации при приблизительно гауссовском распределении априорных вероятностей Pj ≠ 1/N и гауссовских помехах в канале КПДС – статическая формула Шеннона.
Поскольку Г. Найквист доказал (разд. 16), что максимальная скорость телеграфирования (то есть символьная скорость) равна удвоенной частоте среза полосы пропускания линии электросвязи (частоты Найквиста) FН, то пропускная способность многоуровневого телеграфа, или системы передачи дискрет-
ных сообщений с многоуровневой амплитудной манипуляцией N-ASK будет
равна: C(Q) = 2 FН  = FН
= FН 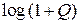 . Это соответствует динамической
. Это соответствует динамической
асимптотической формуле Шеннона для пропускной способности аналогового канала с аддитивным белым гауссовским шумом.
Проведём сравнительные оценки пропускной способности современных каналов КПДС упрощенным способом, аналогичным рассмотренному в разд. 16. За основу сравнительного анализа следует взять многопозиционную фазовую манипуляцию: при N = 4 созвездие 4-PSK является элементарной ячейкой модуляции N-QAM с квадратным созвездием, а при N = 6 – с гексагональным.
В то же время, один уровень модуляции N-QAM с квадратным созвездием формально является «многоуровневым телеграфом»: системой типа «ЦАП–линия электросвязи–АЦП».
Если взять аддитивную помеху, равномерно распределённую на проме-
жутке (– W, + W ], то, как показали численные расчёты (см. разд. 12), с увеличе-
нием N величина ℰ растёт как ℰ = log N до тех пор, пока соседние уровни не
станут находиться на расстоянии Δu друг от друга, равном 2 W. При дальней-
шем увеличении N величина ℰ резко уменьшается: вследствие «перепутыва-
ния» уровней телеграфа, соответствующих выходным символам vk; k = 1, 2, ….
Значит, при равномерно распределённых на промежутке (–W, W ] аддитивных помехах пропускная способность многоуровневого телеграфа есть:
C(Q) = 2 FН log N0 = FН 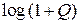 , где N0 =
, где N0 = 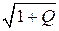 – количество уровней, при ко-
– количество уровней, при ко-
тором расстояние между соседними уровнями Δu становится равным 2 W
(см. статью Найквиста [54]). Как видим, это соответствует пропускной способности системы аналоговой радиосвязи с гауссовским распределением «бесконечного числа уровней» при наличии в канале аддитивного белого гауссовского шума (АБГШ).
Поскольку в современных цифровых системах радиосвязи многопозиционные сигналы представляются созвездием на плоскости {Im, Qn}, то, по аналогии с многоуровневым телеграфом, описываемым одномерным созвездием, сравнительный анализ пропускной способности таких систем можно провести при аддитивных помехах, равномерно распределённых в круге радиуса r. В этом случае пропускная способность Cц(Q) = 2 FН log N0 будет определяться состоянием созвездия N0, при котором расстояния между соседними позициями будет равно величине 2 r.
Средняя мощность такого рода помех есть:
 .
.
Средняя мощность сигнала  определяется конфигурацией созвездия и величиной 2 r, то есть зависит от способа цифровой модуляции сигналов.
определяется конфигурацией созвездия и величиной 2 r, то есть зависит от способа цифровой модуляции сигналов.
Дата добавления: 2015-05-16; просмотров: 1131;
