Каналы с многопозиционной фазовой манипуляцией

Для оценивания пропускной способности каналов КПДС, в которых применяется модуляция N-PSK, воспользуемся методикой, развитой в разд. 12 применительно к «многоуровневому телеграфу».

На рис. 30.в показана геометрия созвездия в канале КПДС и области принятия решения при демодуляции в приёмнике. Количество информации в единицу времени, получаемое на выходе такого канала есть:

. (18.2)

Пусть вторичный источник сообщений не имеет избыточности, то есть P_j = P₁ = 1/N.

Тогда формула (18.2) перепишется как: .

Из рис. 30.в следует, что все величины P_{j j}, P_{j, j ±1}, …, P_{j, j ± N/2} одинаковы (многопозиционный симметричный канал КПДС); поэтому переходная матрица Π = || P_jk; j, k = 1, 2, …, N || – квазидиагональна, а все P_k – одинаковы: .

Значит, формула (18.2) несколько упростится:

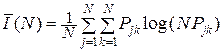. (18.3)

Плотность вероятности вектора 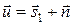, где – сигнал 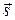в первой позиции сигнального созвездия, можно представить в виде (см. рис. 30.б ):

.

Сделаем замену системы декартовых координат (x, y) на плоскости {U_c ≡ x, U_s ≡ y} на систему полярных координат (ρ, φ): (x = ρ cos φ, y = ρ sin φ).

Элемент площади на плоскости {U_c, U_s} в полярных координатах есть: dx dy = ρ dρ dφ, а плотность вероятности вектора 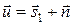имеет вид:

,

или .

Значит, элементы переходной матрицы Π можно вычислять по формуле:

, (18.4)

где Δφ = 2 π /N – величина кванта по начальной фазе несущей радиосигнала.

Вообще говоря, интеграл 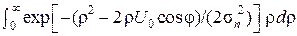сводится к выражению, в которое входит функция erf (a cos φ); однако полученная таким

образом функция первообразной по аргументу φ уже не имеет. Поэтому лучше всего значения элементов P_{j k} получать численным интегрированием по формуле (18.4), содержащей только элементарные функции.

В результате численного интегрирования в соответствии с формулой (18.4) и вычисления величины по формуле (18.3), получаем серию графиков, показанных на рис. 33*⁾.

Из рис. 33 следует, что, как и в случае многоуровневой телеграфии, при гауссовских помехах, в отличие от случая равномерных помех, зависимость величины при данном значении Q от квазинепрерывного аргумента N максимума не имеет. Интуитивно это совершенно ясно: несмотря на «перепу-

*⁾ Вычисления для рис. 33. проведены магистранткой А. С. Шевченко

тывание» позиций созвездия модуляции N-PSK, даже при малых значениях Q, чем больше этих позиций (N → ∞), тем больше информации можно передать по каналу КПДС, хотя при уменьшении отношения сигнал/помеха Q увеличение количества фазовых позиций N становится всё менее и менее эффективным, и возникает задача оптимизации этого количества.

Очевидно, что при Q → ∞ величина R(Q) стремится к значению log N. При N → ∞ мы получаем пропускную способность C_PSK (Q) канала КПДС для случая применения в нём многопозиционной фазовой манипуляции N-PSK. На рис. 33 для сравнения приведены также результаты расчётов по «одномерной статической формуле Шеннона»: C_Ш(Q) = .

Как видим, при больших значениях отношения Q (Q > 30) пропускная способность канала КПДС с модуляцией N-PSK на 1,1 (бит/с) больше, чем пропускная способность канала КПДС с классическими «одномерными» способами модуляции. Это также нетрудно объяснить.

R

бит

с N = ∞

4 C_Ш(Q)16

 

3 8

 

 

2 4

 

 

1 N = 2

 

 

0

Q

Рис. 33. Зависимость от величины Q скорости передачи информации R

динамической системы ДСПИ, использующей фазовую манипуляцию N-PSK

Поскольку на промежутке [– U₀, U₀], являющемся диаметром окружности сигнального созвездия PSK, можно разместить N позиций, то на окружности созвездия PSK можно разместить, при тех же условиях, (π N – 1) позиций.

Это могло бы повысить пропускную способность канала КПДС на log (π N – 1) (бит/с), то есть

Δ 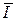= log (π N – 1) – log N = log [(π N – 1)/N] ≈ log π.

Однако воздействие помех при квадратурной обработке сигнала удваиввается. Поэтому фактически Δ 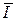≈ log (π/ ) ≈ 1,15 (бит/с).

Зависимость C_PSK (Q) можно аппроксимировать выражением:

C_PSK (Q) ≈ .

Поскольку при Q >> 1 величина C_PSK (Q) на 0,9 (бит/с) больше, чем C_Ш(Q) ≈ (см. рис. 33), то a ≈ 3,6. Поэтому C_PSK (Q) ≈ .

Всё это справедливо при Q → ∞ и N → ∞. Для реальных систем электросвязи, применяющих модуляцию N-PSK, следует выбрать конкретные значения N₀ при заданной величине Q. Для этого можно поступить следующим образом. Заменить гауссовскую помеху эквивалентной ей равномерной; при полученном эквивалентном радиусе r_э равномерной помехи и заданной величине U₀ вычислить эквивалентное отношение сигнал/помеха Q_э; по полученным значениям N₀

и Q_э определить скорость передачи информации по каналу, использующему мо-

N q₀

15

10 5 q₀(Q)|_{I= 3}

q₀(Q)|_{I= 1}q₀(Q)| _{I= 2}

5

0

Q

Рис. 34. Рельеф функции (N, Q) и выбор

оптимального количества уровней N ₀ при модуляции N-PSK

дуляцию N-PSK.

Для реализации этой методики (см. разд. 12) нужно, по данным рис. 33, построить рельеф 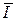(Q, N ), изображённый на рис. 34 «горизонталями». Значение эквивалентного радиуса помехи находим из равенства: 4 π r_э² p_n(0, 0) = 1. Отсюда получаем: r_э = .

Отношение сигнал/помеха для модуляции N-PSK есть: Q = U₀²/(2 σ_n²). При этом N₀ = 2 π U₀/Δφ = 2 π U₀²/(Δφ U₀). Введём обозначение: Δu = Δφ U₀; тогда U₀ = Δu N₀/(2 π).

Значит, Q = Δu² N ²/(4 π² 2 σ_n²), то есть величина оптимального относительного кванта равна: q₀ = Δφ U₀/( σ_n) = 2 σ_n /( σ_n), или q₀ ≈ 2.

На рис. 35 представлены окончательные зависимости от отношения сигнал/шум Q скорости передачи информации R_PSK по каналу КПДС, использующему модуляцию N-PSK, и оптимального количества позиций созвездия N₀ в канале КПДС.

R_PSKN₀

бит

знак

4 40 2 3 4

 

3 30 5

 

 

2 20 1

 

 

1

 

 

0

Q

Рис. 35. Зависимость от величины Q оптимальной скорости

передачи информации R_PSK и оптимального количества позиций N₀

для канала КПДС с модуляцией N-PSK

Для сравнения также показана кривая Шеннона, вычисленная по формуле C_Ш = log (1 + Q)/2. Поскольку количество позиций N₀ не может быть менее двух, то при Q < 1 кривая R(Q) продолжена в соответствии с формулой для вычисления скорости передачи информации в бинарном симметричном канале (см. формулу (9.3) и рис. 11).

Из рис. 35 следует:

– при Q > 30 скорость передачи информации по каналу КПДС с модуляцией N-PSK на 0,8 (бит/с) больше, чем пропускная способность «одномерных каналов КПДС»;

– для величины Q = 10 значение 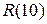= 2,3 (бит/с) при оптимальном количестве фазовых позиций N₀ = 8.

Возможны и другие практические выводы из представленных выше результатов расчётов. Возможны также вычисления скорости передачи информации R_PSK(Q) по каналу КПДС, использующему модуляцию N-PSK, и оптимальное количество позиций созвездия N₀(Q) в канале КПДС при негауссовских и (или) неаддитивных помехах. Причём такие вычисления может произвести квалифицированный радиоинженер-системотехник. В этом и состоит практическая польза информационной теории радиотехнических систем.