Квадратурная амплитудная модуляция

В каналах радиосвязи с квадратурной амплитудной модуляцией [29, 35] радиосигнал в простейшем случае определяется формулой:

s_{m n}(t) = I_m(t) cos (2 π f₀ t) + Q_n(t) sin (2 π f₀ t); m, n = 1, 2, …, 2 M; M = 1, 2, …;

где I_m(t) = (m – M – 1/2) Δu rect(t/τ _э); Q_n(t) = (n – M – 1/2) Δu rect(t/τ _э);

I_m(t) и Q_n(t) – соответственно косинусная и синусная составляющие модулирующего сигнала; f₀ – частота несущей радиосигнала; Δu – расстояние между соседними уровнями (величина кванта) составляющих I_m(t) или Q_n(t); rect(t/τ) – прямоугольный импульс длительностью τ _э с единичной амплитудой; M – порядок квадратного созвездия.

Величины I_m = (m – M – 1/2) Δu и Q_n = (n – M – 1/2) Δu в совокупности образуют сигнальное созвездие порядка M на плоскости {x = I, y = Q}.

Определим отношение сигнал/помеха Q в канале КПДС. Пусть источник независимых дискретных сообщений (ДИС), поступающих в канал, не имеет информационной избыточности. Тогда все N = 4 M ² радиосигналов {s_{m n}(t)} будут равновероятными, а средняя эквивалентная мощность радиосигналов P_кв(M ) в канале КПДС определится выражением [см. формулу (18.1)]:

P_кв(M ) = ,

или P_кв(M ) = .

В результате проведения суммирования по i' и l', получим:

P_кв(M ) = Δu² (2 M + 1) (2 M – 1)/6.

Если максимальная амплитуда радиосигнала в канале КПДС ограничивается значением U₀, то величина кванта Δu будет связана с величиной U₀ выражением: U₀² = (2 M – 1)² Δu²/2.

Поэтому, окончательно получаем:

P_кв(M ) = 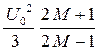. (18.5)

Например, при M = 1 (четырёхпозиционная модуляция 4-QAM или фазовая манипуляция 4-PSK ): P_кв(M ) = P_кв(1) = 3U₀²/3 = U₀², что очевидно.

При M → ∞ из формулы (18.5) получаем: P_кв(M ) = P_кв(∞) = U₀²/3, что соответствует дисперсии равномерного распределения случайной величины на квадрате с диагональю длиной 2 U₀.

Что касается помех в канале КПДС, то будем считать их аддитивным белым гауссовским шумом (АБГШ). Тогда в результате оптимальной квадратурной обработки сигналов {s_{m n}(t)} в канале КПДС к величинам I_m и Q_n добавятся случайные независимые гауссовские величины с нулевыми средними и одинаковыми дисперсиями σ_n².

Значит, воздействие помех на сигнальное созвездие {I_m, Q_n} можно выразить двумерным случайным вектором на плоскости {x, y}, имеющим плотность

вероятности p_n(x, y) = .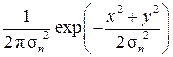

Средняя мощность таких помех:

P_n = .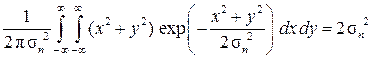

Таким образом, отношение сигнал/помеха Q в канале КПДС с квадратным созвездием N-QAM с учётом формулы (18.5) есть:

Q = .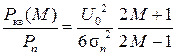

Скорость передачи информации R (U, П) определяется средним на один знак источника ДИС количеством информации 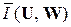, которое получается на выходе канала КПДС в единицу времени, и вычисляется по формуле:

R _ц(U, П) = /τ _э = ,

где 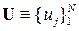– совокупность знаков источника ДИС;

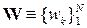– совокупность символов на выходе канала КПДС;

– среднее количество информации на выходе канала КПДС;

τ _э – длительность элементарной посылки;

P_j – априорная вероятность выдачи источником ДИС элементарного сообщения (знака) u_j;

P_jk – условная вероятность того, что при поступлении знака u_j демодулятор канала КПДС выдаст решение о приёме символа w_k, то есть P_{j k} = P(w_k |u_j);

P_k – полная вероятность того, что демодулятор примет решение о приёме символа w_k; .

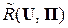В дальнейшем будем считать величину τ _э равной некоторой единице времени; так что величина R (U, П) численно равна величине (бит/знак). Величину = R _ц(U, П)/τ _э = будем называть относительной скоростью передачи информации в динамической системе передачи сообщений.

Если избыточность источника снята (кодером источника), то P_j = 1/N, 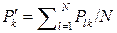, и относительную скорость 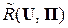можно вычислять по формуле:

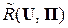= = , (18.6)

Скорость передачи информации 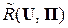зависит от допустимой величины U₀ в канале КПДС, от величины кванта Δu и от мощности помех P_n = 2 σ_n² в канале. При больших значениях Q (Q → ∞) скорость 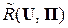определяется количеством позиций N = 4 M ² в созвездии QAM:

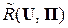= log N = 2 log (2 M ) = 2 log N ⁽¹⁾ = 2 ,

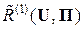где N ⁽¹⁾ ≡ 2 M – число косинусных либо синусных составляющих модуляции N-QAM; 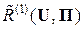– скорость передачи информации с помощью только косинусных либо только синусных составляющих (N-позиционная биполярная амплитудная манипуляция N-ASK); 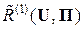= log N ⁽¹⁾.

Значит, при Q → ∞ число позиций сигнального созвездия N-QAM составляет N ≈ [N ⁽¹⁾]², а скорость передачи информации 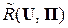≈ 2 .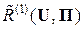

Если отдельно рассмотреть канал КПДС, использующий только косинусные либо только синусные составляющие N-QAM, то мы придём к классической задаче оценки пропускной способности канала связи с ограниченной пиковой мощностью [46], в которой эквивалентная пиковая мощность равна = U₀²/2, а мощность помех 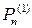= σ_n². В этом случае средняя мощность радиосигналов равна P_s(M ) = Δu² (2 M + 1) (2 M – 1)/12, а отношение сигнал/поме-

ха:

= .

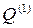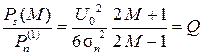Следовательно, при заданном порядке M квадратного сигнального созвездия N-QAM и при любом конечном значении величины Q (1 < Q < ∞) в канале КПДС скорость передачи информации 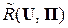почти в два раза больше, чем в канале КПДС, использующем только косинусные либо только синусные составляющие при том же значении отношения сигнал/помеха: 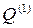= Q.

Поэтому расчёты пропускной способности каналов КПДС, использующих квадратные созвездия N-QAM, для простоты вычислений, можно свести к задаче оценки пропускной способности канала связи с ограниченной пиковой мощностью, для которой в своё время К. Шеннон получил асимптотические ограничения сверху и снизу (теорема 20 в [46]). Компьютерные численные расчёты (по методике, развитой в разд. 12) позволяют уточнить и конкретизировать эту оценку (учесть отсутствие крайних позиций созвездия N-QAM, не-гауссо-вость и не-белость аддитивных помех и т. п.) и применить результаты таких расчётов для оценки пропускной способности каналов КПДС, использующих модуляцию N-QAM.

Мы же проведём оценку пропускной способности каналов КПДС с модуляцией N-QAM, воспользовавшись результатами, которые были получены в разд. 12. В этом случае получим зависимости от отношения Q оптимальной скорости передачи информации 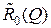по каналу КПДС с квадратурной амплитудной модуля цией N-QAM при величине кванта Δu₀ = 2,5 σ_n и оптимального количества соответствующих позиций созвездия N₀(Q) (кривые 1 и 2 на рис. 36).

Эти зависимости можно аппроксимировать функциями:

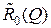≈ 2 ≈ log (1 + 0,55 Q), N₀(Q) ≈ [ 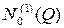]² ≈ 1 + 1,9 Q.

Пользуясь такими аппроксимациями можно, например, определить, что модуляцию 64-QAM лучше всего применять при отношении сигнал/помеха в канале КПДС Q ≈ 33. В этом случае скорость передачи информации составляет 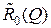≈ 4,25 бит/с.

Поскольку при N = 4 канал КПДС с квадратурной модуляцией N-QAM – симметричный (см. рис. 30.а), а количество уровней N-QAM не может быть меньше, чем четыре, то скорость передачи канала КПДС с модуляцией N-QAM при Q < 2 можно в точности оценить аналитически, удвоив пропускную способность симметричного бинарного канала КПДС (см. разд. 10, рис. 11).

I_пр N₀

бит

с

8 400 31

6 300 2

Q

Рис. 36. Зависимости от отношения сигнал/помеха Q

оптимальной скорости передачи информации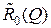

и количества уровней N₀ для каналов КПДС с модуляцией N-QAM

Таким образом, уточнению численными компьютерными способами пропускной способности канала КПДС с модуляцией N-QAM подлежит участок кривой 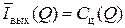при значениях аргумента 2 < Q < 8 (см. рис. 36). Для сравнения и аппроксимации на рис. 36 приведены результаты расчётов по «двумерной асимптотической формуле Шеннона» .

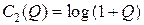Итак, мы рассмотрели и проиллюстрировали на конкретных примерах методику расчёта пропускной способности , оптимального количества уровней 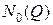и информационной надёжности 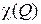как для классических каналов КПДС с «одномерными» методами модуляции, так и для современных каналов КПДС с «двумерными» методами многопозиционной цифровой модуляции: фазовой N-PSK, амплитудной N-QAM с квадратными, гексагональными и другими видами сигнальных созвездий. Эти результаты являются итоговыми в ПРИКЛАДНОЙ ТЕОРИИ ИНФОРМАЦИИ.

Вопросы для самопроверки

1. Каковы основные методы цифровой модуляции, используемые в современных каналах электросвязи?

2. Каковы основные виды сигнальных созвездий, используемые в современных системах радиосвязи?

3. Какова теоретическая пропускная способность каналов радиосвязи с квадратурной амплитудной модуляцией?

4. Каковы сравнительные информационные характеристики каналов радиосвязи, использующих современные цифровые методы модуляции?

5. Каким образом вычисляется пропускная способность, оптимальное количество сигнальных позиций и коэффициент информационной надёжности радиоканалов с многопозиционной фазовой манипуляцией?

6. Какова полная зависимость информационных характеристик канала радиосвязи с многопозиционной фазовой манипуляцией?

7. Каким образом вычисляется пропускная способность, оптимальное количество сигнальных позиций и коэффициент информационной надёжности радиоканалов с многопозиционной квадратурной амплитудной модуляцией?

8. Какова полная зависимость информационных характеристик канала радиосвязи с многопозиционной квадратурной амплитудной модуляцией?

ЗАКЛЮЧЕНИЕ

Математическая теория информации (МТИ), как и многие разделы современной математики, родилась из попыток общего решения конкретных прикладных задач: теоретическая оценка максимальной скорости передачи сообщений по различным каналам связи при наличии в последних различного рода помех и разработка методов повышения эффективности их использования и их надёжности. В силу исключительной математической интуиции Клода Шеннона и благодаря выдающимся «чистым математикам» математическая теория информации стала частью теории вероятностей, основанной на весьма абстрактной теории меры Лебегом и интеграла Стилтьеса.

Попытки перенести фундаментальные результаты теории МТИ на инженерный уровень изложения, доступный для усвоения методов математической теории информации студентами технических специальностей, наталкиваются на отличную от «чистых теоретиков» математическую подготовку будущего инженера (классические дифференциальное и интегральное исчисление, «обычная» теория вероятностей и математическая статистика) и совершенно иную, чем это требует МТИ, логику инженерного мышления (конктетность, простота и наглядность). Поэтому, оставаясь на позиции прикладной теории информации (ПТИ), из которой собственно и выросла теория МТИ, следует идти по пути, намеченному инженерами Гарри Найквистом и Ральфом Хартли.

Найквист и Хартли первыми осознали, что скорость передачи знаковых (дискретных, семиотических) сообщений пропорциональна полосе пропускания канала связи и логарифму числа уровней напряжения или тока, используемому для передачи дискретной информации с помощью аналоговых каналов связи.

Клод Шеннон обобщил идеи Найквиста и Хартли в двух основных направлениях:

1. распространил формулу Хартли на не-равновероятные знаки алфавита («энтропия» источника дискретных сообщений);

2. предложил формулу для оценки степени потери информации в каналах передачи дискретных сообщений при наличии в этих каналах помех («остаточная неопределённость» на выходе канала связи и взаимная энтропия входа и выхода канала КПДС).

Уже как следствие – из формально-математической постановки задачи оценивания максимально возможной скорости передачи информации по многоуровневому каналу связи с полосой пропускания B и с гауссовскими шумами – вытекает знаменитая асимптотическая формула C ≈ B log ₂ (1 + P/N ), где P – мощность сигнала; N – мощность шума; 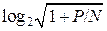– количество «чётко различимых уровней» Найквиста (информационная статика – проблема квантования); 2 B – максимальная «скорость телеграфирования» (информационная динамика – проблема дискретизации).

Однако эта красивая формула справедлива при больших значениях отношения сигнал/шум (Q = P/N > 3-7) и «одномерных» методах передачи сообщений в системах проводной электросвязи.

Тем самым в приближённом виде решается центральная задача теории ПТИ, поставленная Г. Найквистом в 1924 г. Более точные оценки информационной ёмкости различных статических и пропускной способности динамических каналов КПДС, как показано в данном учебном пособии, достаточно просто можно получить численными расчётами. Результаты такого рода расчётов показывают, что в современных цифровых системах электросвязи получают скорости передачи информации, почти в два раза бóльшие, чем это следует из «одномерной» формулы Шеннона.

Математическая подготовка студентов инженерных специальностей вполне достаточна не только для понимания основ прикладной теории информации как информационной теории радиосистем, но и для самостоятельного применения методов и результатов теории ПТИ при постановке и решении конкретных инженерных задач, как это делают студенты в процессе изучения других дисциплин их специальности.

Это утверждение справедливо при условии, что преподавание прикладной теории информации будет основываться не на абстрактно-математической теории меры Лебега и интеграла Стилтьеса, как это делается в математической теории информации в привычном для «чистых математиков» стиле (определения, леммы, теоремы, доказательство их непротиворечивости, следствия и т. д.) при игнорировании возможности практического применения результатов теории МТИ, а на классических дифференциальном и интегральном исчислении, линейной алгебры, а также на обычной теории вероятностей и математической статистике, как это принято в высших технических учебных заведениях при преподавании других инженерных дисциплин (постановка конкретной инженерной задачи, возможные подходы к её решению, подробный вывод соответствующих формул, осмысление полученных результатов, способы их практической реализации, наконец – только в заключение – обобщение полученных результатов на более сложные случаи).

При изложении прикладной теории информации как информационной теории радиотехнических систем автор настоящего учебного пособия старался придерживаться именно этих методологических принципов. Как это ему удалось – судить читателю.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Адаменко, А. Н. Информационно-управляющие человеко-машинные системы: Исследование, проектирование, испытания: Справочник /А. Н. Адаменко, А. Т. Ашеров, И. Л. Бердников и др. – М.: Машиностроение, 1993. – 528 с.

2. Анцев, Г. В. Основы теории информации: учеб. пособие / Г. В. Анцев, В. П. Ипатов, И. М. Самойлов; под ред. В. П. Ипатова. – СПб.: Агентство «ВиТ-принт», 2004. – 112 с.

3. Бриллюэн, Л. Научная неопределённость и информация / Л. Бриллюэн – М.: КомКнига, 2006. – 272 с. (переиздание 1966 г.).

4. Быховский, М. А. Круги памяти. Очерки истории развития радиосвязи и вещания в XX столетии / М. А. Быховский. – М.: МЦНТИ, ООО «Мобильные коммуникации», 2001. – 224 с.

5. Быховский, М. А. Пионеры информационного века. История развития теории связи / М. А. Быховский. – М.: ЗАО «РИЦ “Техносфера”», 2006. – 376 с.

6. Васин, В. А. Радиосистемы передачи информации: учеб. пособие / В. А. Васин, В. В. Калмыков, Ю. Н. Себекин и др. – М.: Горячая линия-Телеком, 2005. – 472 с.

7. Вентцель, Е. С. Теория вероятностей и её инженерные приложения / Е. С. Вентцель, Л. А. Овчаров. – М.: Академия, 2003. – 458 с.

8. Вероятность и математическая статистика: Энциклопедия / Гл. ред. Ю. В. Прохоров. – М.: Большая Российская Энциклопедия, 1999. – 910 с.

9. Весоловский, К. Системы подвижной радиосвязи. Пер. с польск. под ред А. И. Ледовского / К. Весоловский. – М.: Горячая линия-Телеком, 2006. – 536 с.

10. Винер, Н. Кибернетика, или Управление и связь в животном и машине / Н. Винер. – М.: Наука, 1983. – 341 с.

11. Владимиров, В. С. Обобщённые функции в математической физике / В. С. Владимиров. – М.: Наука, 1979. – 320 с.

12. Вудворд, Ф. М. Теория вероятностей и теория информации с применениями в радиолокации / Ф. М. Вудворд. – М.: Сов. радио, 1955. – 128 с.

13. Галлагер, Р. Теория информации и надёжная связь / Р. Галлагер. – М.: Сов. радио, 1974. – 719 с.

14. Голдман, С. Теория информации / С. Голдман. – М.: Изд-во ИЛ, 1957. – 446 с.

15. Дмитриев, В. И. Прикладная теория информации / В. И. Дмитриев. – М.: Высш. шк., 1989. – 319 с.

16. Колесник, В. Д. Курс теории информации / В. Д. Колесник, Г. Ш. Полтырев. – М.: Наука, 1982. – 416 с.

17. Колмогоров, А. Н. Sur l'interpolation et extrapolation de suits stationaires// C. R. Acad. Sci., t. 208, 1939. – P. 2043-2045. Он же: Интерполирование и экстраполирование стационарных случайных последовательностей // Изв. АН СССР (сер. матем.), т. 5, 1941, № 1. – С. 3-14.

18. Колмогоров, А. Н. Теория передачи информации / А. Н. Колмогоров. – М.: Изд-во АН СССР, 1956. – 33 с.

19. Конторов, Д. С. Радиоинформатика /Д. С. Конторов, М. Д. Конторов, В. К. Слока. – М.: Радио и связь, 1993. – 294 с.

20. Корн, Г. Справочник по математике для научных работников и инженеров. Определения, теоремы, формулы / Г. Корн, Е. Корн. – СПб.: Лань, 2003. – 831 с.

21. Котельников, В. А. О пропускной способности «эфира» и проволоки в электросвязи. (Материалы к I Всесоюзн. съезду по вопросам технич. реконструкции дела связи и развития слаботочной пром-сти.) – М.: Изд-во Управления связи РККА, 1933. – 19 с. (Сдано в набор 19.11.1932 г. Факсим. переизд.: «Радиотехника», 1995, № 4-5. – С. 42-55. Отред. переизд.: УФН, т. 176, 2006, № 7. – С. 762 – 770.)

22. Лачинов, В. М. Информодинамика, или Путь к Миру открытых систем / В. М. Лачинов, А. О. Поляков. – СПб.: Изд-во СПбГТУ, 1999. – 431 с.

23. Печинкин, А. В. Теория вероятностей /А. В. Печинкин, О. И. Тёскин, Г. М. Цветкова и др. – М.: Изд-во МГТУ, 2001. – 456 с.

24. Пирс, Дж. Символы, сигналы, шумы. Закономерности и процессы передачи информации / Дж. Пирс. – М.: Мир, 1967. – 335 с. (Оригинал: 1962 г.)

25. Пирс, Ч. Логические основания теории знаков / Ч. Пирс. – СПб.: СПб ГУ, Алетейя, 2000. – 352 с.

26. Плошко, Б. Г. История статистики / Б. Г. Плошко, И. И. Елисеева. – М.: Финансы и статистика, 1990. – 295 с.

27. Родионов, В. М. Зарождение радиотехники / В. М. Родионов. – М.: Наука, 1985. – 240 с.

28. Семиотика: Антология /Сост. Ю. С. Степанов. – М.: Академ. проект; Екатеринбург: Деловая книга, 2001. – 702 с.

29. Скляр, Б. Цифровая связь. Теоретические основы и практические применения/ Б. Скляр. – М.: Изд. Дом «Вильямс», 2007. – 1104 с.

30. Степанов, Ю. С. Семиотика / Ю. С. Степанов. – М.: Наука, 1971. – 168 с.

31. Теория передачи информации. Терминология. – М.: Наука, 1984. – 32 с.

32. Уилкс, С. Математическая статистика / С. Уилкс. – М.: Наука, 1967. – 632 с.

33. Файнстейн, А. Основы теории информации / А. Файнстейн. – М.: Изд-во ИЛ, 1960. – 140 с.

34. Фано, Р. Передача информации. Статистическая теория связи / Р. Фано. – М.: Изд-во Мир, 1965. – 439 с.

35. Феер, К. Беспроводная цифровая связь. Методы модуляции и расширения спектра/ К. Феер. – М.: Радио и связь, 2000. – 500 с.

36. Фишер, Р. А. Статистические методы для исследователей / Р. А. Фишер. – М.: Госстатиздат, 1958. – 268 с.

37. Функции с двойной ортогональностью в радиоэлектронике и оптике. США, 1961-1968 гг./ Пер. и науч. обработка М. К. Размахнина и В. П. Яковлева. – М.: Сов. радио, 1971. – 256 с.

38. Хармут, Х. Применение методов теории информации в физике / Х. Хармут. – М.: Изд-во Мир, 1989. – 319 с.

39. Худяков, Г. И. Теорема отсчётов теории сигналов и её создатели // Радиотехника и электроника. – 2008. – № 9. – C. 1157-1167.

40. Худяков, Г. И. Теорема отсчётов для цифровой обработки случайных сигналов // Компоненты и технологии. – 2009. – № 5.– C. 110-113.

41. Худяков, Г. И. Оценка пропускной способности каналов авиационной цифровой электросвязи// Электросвязь. – 2009. – № 5. – С. 37-38.

42. Худяков, Г. И. Статистическая теория радиотехнических систем: Учеб. пособие / Г. И. Худяков. – М.: Изд. центр «Академия», 2009. – 400 c.

43. Худяков, Г. И., Осипов А. Д. Сравнительная оценка пропускной способности современных цифровых каналов радиосвязи // Радиоэлектроника интеллектуальных транспортных систем: Научно-техн. сб. Вып 2. СПб.: Изд-во СЗТУ, 2009.– С.7-13.

44. Худяков, Г. И. Пропускная способность цифровых каналов электросвязи с квадратурной амплитудной модуляцией // Электросвязь. – 2010. № 6. – С.11-13.

45. Хэмминг, Р. В. Теория кодирования и теория информации/ Р. В. Хэмминг. – М.: Радио и связь, 1983. – 174 с.

46. Шеннон, К. Работы по теории информации и кибернетике. Пер. с англ. под ред Р. Л. Добрушина и О. Б. Лупанова / К. Шеннон. – М.: Изд-во ИЛ, 1963. – 830 с.

47. Шишкин, И. Ф. Теоретическая метрология. Ч I. Общая теория измерений / И. Ф. Шишкин. – СПб.: Изд-во СЗТУ, 2008.– 189 с.

48. Яроцкий, А. В. Основные этапы развития телеграфии / А. В. Яроцкий. – М.-Л.: Госэнергоиздат, 1963. – 80 с.

49. Carson, J. R. The Statistical Energy-Frequency Spectrum of Random Disturbances // Bell Syst. Tech. J., v. 10, 1931, № 3. – P. 374-381.

50. Hartley, R. V. L. Transmission of information // Bell Syst. Tech. J., v. 7, 1928, № 3. – P. 535-563. (Рус. пер.: «Теория информации и её приложения (Сборник переводов)»/ Под ред. А. А. Харкевича. – М.: Физматгиз, 1959. – С. 5-35.)

51. Küpfmüller, R. Über die Dynamik der selbsttätigen Verstärkungstregler // Elektrische Nachrichten-Technik, Bd. 5, 1928, № 11. – S. 459-467.

52. Millman, S. (Ed.) A History of Engineering end Science in the Bell System: Communication Sciences (1925-1980). – AT&T Bell Laboratories, 1984. – 522 p.

53. Nyquist, H. Certain Factor Affecting Telegraph Speed // Bell. Syst. Tech. J., v. 3, 1924, № 2. – P. 324-346.

54. Nyquist, H. Certain Topics in Telegraph Transmission Theory// Trans. AIEE, v. 47, 1928, № 2. – P. 617-644. (Репринт. изд.: Proc. IEEE, v. 90, 2002, № 2. – P. 280-305.)

55. Nyquist, H. Thermal Agitation of Electric Charge in Conductors // Phys. Rev., v. 32, 1928, № 1. – P. 110-113.

56. Rice, S. O. Mathematical Analysis of Random Noise // Bell Syst. Tech. J. Part I: v. 23, 1944, № 3. – P. 282-332. Part II: v. 24, 1945, № 1. – P. 46-156. (Рус. пер.: «Теория передачи электрических сигналов при наличии помех»/ Сб. пер. под ред. Н. А. Железнова. – М.: Изд-во ИЛ, 1953. – С. 88-238.)

57. Tuller, W. G. Theoretical limitations on the rate of transmission of information // Proc. IRE, v. 37, 1949, № 5. – P. 468-478. (Рус. пер.: Теория информации и её приложения (Сб. переводов). Под ред. А. А. Харкевича. – М.: Физматгиз, 1959. – С. 58-81.)

58. Whittaker, E. T. On the Function which are represented by the Expansion of the Interpolation-Theory // Proc. Roy. Soc. Edinburgh, v. 35, pt. 2, 1914-15. – P. 181-194.

59. Wiener, N. The interpolation, extrapolation and smoothing of stationary time series / N. Wiener. – New York: Wiley, 1949. – 160 p.

60. Ресурсы Интернет: www.ru.wikipedia.org; www.en.wikipedia.org.