XI x0 xII x

Рис. 13. Априорная p₀(x) и апостериорная p_I(x)

плотности вероятности величины x₀

Отсюда среднее значение 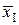и дисперсия D_I результата однократного измерения суть:

,

или ;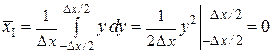

,

или D_I/Δ x ² = 1/12, σ_I = ≈ 0,288 Δ x, где y = x – x_I.

Если мы проведём серию из n независимых измерений, то в результате округления получим выборку 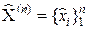, имеющую вид (x_I, x_I, …, x_I).

Значит, оптимальная оценка 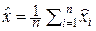= x_I останется по-прежнему несмещённой, но будет иметь ту же дисперсию D_Σ = Δ x ²/12, то есть неопределённость оценки 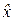не уменьшается с увеличением объёма выборки n.

Интуитивно это вполне понятно: сколько ни производи повторных измерений, а с помощью школьной линейки не получить микронной точности!

Но тогда возникает метрологическая задача: сколько нужно провести сеансов измерений величины x₀ при наличии случайных помех измерениям с помощью данного измерительного прибора, имеющего цену деления шкалы Δ x, чтобы реализовать точность этого прибора?

Для рассмотренной нами информационной меры Р. Фишера эта задача решается элементарно. Поскольку предельная информативность прибора ограничивается дискретностью Δ x, то есть величиной I_мин = 12 /Δ x ², а удельная информативность процедуры измерения составляет величину 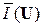, то необходимое количество процедур n определяется уравнением:

I_мин = n 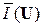, или 12/Δ x ² = n .

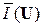Отсюда получаем n ≥ 12/[ 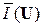Δ x ²].

Например, если помехи приводят к независимым равноточным результатам измерений x₁, x₂, …, x_n величины x₀ с априорной неопределённостью σ₀, то 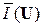= σ₀^–2, а потому n ≥ 12 (σ₀ /Δ x)^–2.

Вопросы для самопроверки

1. Какое противоречие возникает при формально-математическом обобщении энтропии источника дискретных сообщений на источники измерительной (метрологической) информации?

2. Каковы особенности дифференциальной энтропии источника измерительной (метрологической) информации?

3. Каковы основные постулаты для измерительной (метрологической) информации?

4. Что является количественной мерой измерительной (метрологической) информации?

5. Что такое обобщённая дисперсия Уилкса?

6. Каким образом решается информационная проблема округления в теоретической метрологии?