Абсолютные значения энтропии

Постулат Планка используется при термодинамическом исследовании химических процессов для вычисления абсолютных значений энтропии химических соединений -величин, которые имеют большое значение при расчете химических равновесий.

Энтропия твердого вещества вычисляется по уравнению (II, 25):

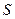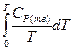= (II,26)

Для вычисления необходимо знать экспериментальные значения теплоемкости, определенные до возможно более низких температур. Значение теплоемкости до 0 К находят путем экстраполяции по уравнению Дебая, либо с помощью эмпирических приемов. Если минимальную температуру, при которой определено значение теплоемкости, обозначить Т*, то можно определить значение коэффициента a’ в уравнении Дебая, приравняв выражение для теплоемкости твердого тела по закону Т – кубов и выражение для теплоемкости в виде степенной функции (I,15), считая, что при Т* они равны:

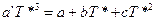
Принимая во внимание, что в приведенном уравнении известны все величины, кроме коэффициента a’, его легко определить. Тогда интеграл (II, 25) можно разложить на два:

=

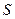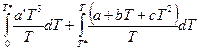
При переходе в жидкое состояние при нормальной температуре плавления энтропия возрастает на величину приведенной теплоты плавления. Нагреванию жидкости отвечает увеличение энтропии, вычисляемое по уравнению (II, 25), причем в подынтегральную функцию входит теплоемкость жидкости:

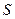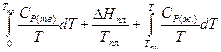= (II,27)

Испарению жидкости при постоянном давлении (например, при Р = 760 мм рт. ст.) и нагреванию газа соответствует увеличение энтропии, аналогично тому, как это имеет место при плавлении твердого тела и нагревании жидкости. Таким образом, уравнение для вычисления энтропии газа при некоторой температуре Т будет иметь вид:

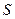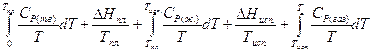= (II,28)

По этому уравнению можно вычислить энтропию идеального газа при температуре Т и 1 атм (если испарение проводилось при нормальной температуре кипения).

В том случае, когда вещество в твердом состоянии имеет не одну, а две или более модификации, в правой части уравнения (II,26) добавятся соответствующие члены - прирост энтропии при переходе первой модификации во вторую, прирост энтропии при нагревании второй модификации и т. д.

Интегральные члены уравнения (II,26) можно найти графически. Для этого строят кривые С_Р/Т=φ(Т) и численное значение интеграла определяют по величине площади, ограниченной кривой и осью абсцисс, заключенными между соответствующими температурами.

Величина энтропии сложным образом отражает всю совокупность свойств соединения в данном его агрегатном состоянии. Энтропия веществ зависит от молекулярной массы (увеличивается с ее ростом в ряду близких по свойствам веществ), от агрегатного состояния веществ (возрастает при переходе от твердых тел к жидким и особенно к газообразным), а также от кристаллического строения, изотопного состава и структуры молекул.