Второй закон термодинамики

Наиболее часто встречающимися и безусловно самопроизвольными являются процессы передачи теплоты от горячего тела к холодному (теплопроводность) и перехода работы в теплоту (трение). Многовековая житейская, техническая и научная практика человечества показали повседневную реальность этих процессов, а также невозможность самопроизвольного протекания обратных процессов, очень заманчивых с практической точки зрения (получение работы за счет отнятия теплоты у тел, окружающих рабочее тело). Это дает основание утверждать, что единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретого тела к более нагретому (постулат Клаузиуса).

Обратный указанному переход теплоты от более нагретого тела к менее нагретому – это обычный неравновесный процесс передачи теплоты путем теплопроводности. Он не может быть обращен, т. е. проведен в обратном направлении через ту же последовательность состояний. Но этого мало: если в системе прошел процесс прямой передачи теплоты, то никаким образом нельзя осуществить такую последовательность любых процессов, в результате которой все тела, участвовавшие в передаче теплоты, пришли бы в исходное состояние и не произошло бы никаких изменений в других телах. Процесс теплопроводности необратим.

Другое общее положение, имеющее ту же опытную основу, утверждает следующее: единственным результатом любой совокупности процессов не может быть превращение теплоты в работу (т. е. поглощение системой теплоты из окружающей среды и отдача эквивалентной этой теплоте работы). Таким образом, самопроизвольный процесс превращения работы в теплоту (путем трения) необратим (так же, как и теплопроводность).

Последнее утверждение может быть изложено иначе: теплота наиболее холодного из участвующих в процессе тел не может служить источником работы (постулат Томсона).

Оба положения (постулаты Клаузиуса и Томсона) являются формулировками второго закона термодинамики и эквивалентны друг другу, т. е. каждое из них может быть доказано на основании другого.

Так как переход теплоты или её превращение в работу рассматривается как единственный результат процесса, то очевидно необходимо, чтобы система, участвующая в теплообмене, возвращалась в результате процесса или совокупности процессов в первоначальное состояние. При таком циклическом процессе внутренняя энергия системы не изменится.

Предположим, что вторая из приведенных выше формулировок (особенно в последней ее форме) неправильна. Тогда можно было бы построить машину, работающую циклами, «рабочее тело» которой периодически возвращалось бы в исходное состояние, причем эта машина давала бы работу за счёт теплоты, поглощаемой извне от тела, не более нагретого, чем сама система и все другие окружающие систему тела. Такой процесс протекал бы без нарушения первого закона термодинамики (работа за счет теплоты), но для практики он равноценен получению работы из ничего, так как всякая машина имела бы практически неисчерпаемый источник теплоты в окружающей среде. Так пароход мог бы двигаться, отнимая теплоту океанской воды и не нуждаясь в топливе. Такая машина называется перпетуум мобиле (вечный двигатель) второго рода. Исходя из этого определения, можно сформулировать второй закон термодинамики, придав постулату Томсона иную форму: перпетуум мобиле второго рода невозможен.

Следует подчеркнуть, что как положения Клаузиуса и Томсона, так и утверждение о невозможности перпетуум мобиле второго рода не доказываются на основании других законов или положений. Они являются предположениями, которые оправдываются всеми следствиями, из них вытекающими, но не могут быть доказаны для всех возможных случаев.

Теорема 1: Для того, чтобы криволинейный интеграл 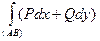не зависел от пути интегрирования, необходимо и достаточно, чтобы дифференциальное выражение (Pdx + Qdy) было в рассматриваемой области точным дифференциалом от некоторой однозначной функции двух переменных.

Теперь естественно, возникает вопрос, по какому признаку можно установить, является ли предложенное дифференциальное выражение точным дифференциалом или нет.

Для того, чтобы получить этот признак в простой и удобной форме, мы дополнительно предположим, что в рассматриваемой области существуют и непрерывны обе частные производные: 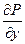и .

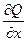При этом предположении искомый признак получается сразу. Если дифференциальное выражение есть дифференциал некоторой функции F(x,y), так что имеют место равенства:

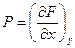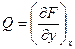и , то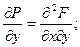

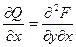
Предполагаемая непрерывность частных производных 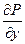и 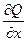обеспечивает равенство двух смешанных производных, следовательно,

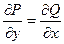
Таким образом, это замечательное по простоте соотношение оказывается необходимым и достаточным условием для того, чтобы дифференциальное выражение (Pdx + Qdy) было точным дифференциалом.

Установим, какое количество теплоты δQ нужно затратить, чтобы перевести газ из состояния (P,V,T) в бесконечно близкое состояние (P+dP, V+dV, T+dT).

δQ = PdV + С_vdT

Исключим из этого уравнения dT. Для этого продифференцируем уравнение Менделеева-Клапейрона:

PdV + VdP = RdT

и определим из него dT:

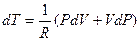
После подстановки получим:

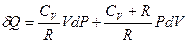
Принимая во внимание, что С_V + R = C_P , окончательно получим:

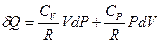и

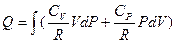
Полученное уравнение позволяет утверждать, что теплота Q не является функцией состояния и зависит от пути процесса, который к этому состоянию привел, т.к. условие интегрируемости здесь явно нарушено:

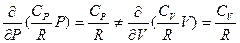
т.к. .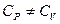

Однако, если выражение для элементарной теплоты умножить на 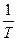, где 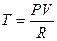есть абсолютная температура, то придем к выражению:

,

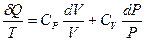которое явно представляет собой полный дифференциал. Первообразной здесь служит функция, которую мы обозначим S:

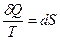
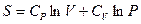
Криволинейный интеграл 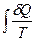уже не зависит от пути интегрирования и отличается от указанной выше функции S лишь постоянной.

Полученный нами результат даёт косвенное доказательство существования некой новой функции состояния, названной энтропией, а также её количественной меры.

Дальнейшие исследования позволили дать ещё одну формулировку второго закона термодинамики, являющуюся, безусловно, достаточно точной и краткой. В ней содержится постулат о существовании уже названной нами новой функции состояния, через которую выражается различие между обратимыми и необратимыми процессами:

Существует функция состояния термодинамической системы – энтропия. При обратимых процессах в изолированной системе её энтропия не изменяется, а при необратимых (самопроизвольных) – увеличивается.

Указанный количественный критерий направления процесса также может быть найден путём исследования цикла Карно с использованием основных формулировок второго закона термодинамики.

Для этого докажем две важные теоремы.

Теорема Карно-Клаузиуса: коэффициент полезного действия тепловой машины, работающей обратимо по циклу Карно, не зависит от природы рабочего тела машины, а лишь от температуры нагревателя и температуры холодильника.

Рассмотрим две машины – 1 и 2 (рис.2), рабочими телами в которых являются два разных вещества. Обе машины работают в одном и том же интервале температур от Т₁ (нагреватель) до Т₂ (холодильник).

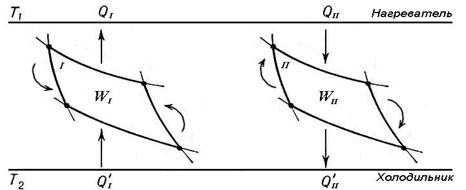
Рис.2. Схема для доказательства теоремы Карно-Клаузиуса.

Машина 1 работает равновесно и обратимо. Заставив машину 1 работать в обратном направлении, а машину 2 в прямом направлении, подберём размеры машин так, чтобы производимые ими работы были равны по абсолютной величине (т.е. так, чтобы площади циклов на диаграмме P – V были равны): 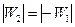. Пусть при этом теплота, получаемая рабочим телом машины 2 у нагревателя, и теплота, отдаваемая им холодильнику, равны Q₂ и Q’₂, а теплота, отдаваемая рабочим телом машины 1 нагревателю, и теплота, получаемая им от холодильника, равны Q₁ и Q’₁ соответственно.

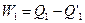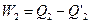Так как , а , то

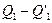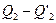= (II,1)

Предположим, что коэффициент полезного действия (кпд) 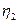машины 2 больше, чем кпд 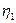машины 1, т.е.

>

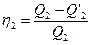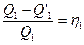
Принимая во внимание уравнение (II,1), получаем:

Q₁ > Q₂ Q’₁ > Q’₂

Пусть обе машины работают совместно так, что работа 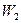, полученная в машине 2, затрачивается в машине 1. При этом нагреватель отдаёт машине 2 теплоту Q₂, и получает от машины 1 теплоту Q₁. Так как Q₁ > Q₂, то в итоге нагреватель получает теплоту

(Q₁ - Q₂). Холодильник отдает теплоту (Q’₁ – Q’₂), равную (Q₁ - Q₂). Суммарная же работа обеих машин равна нулю 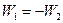. Таким образом, единственным результатом совместного действия двух машин является перенос теплоты от холодильника к нагревателю. По второму закону термодинамики (формулировка Клаузиуса) это невозможно и, следовательно, предположение, что 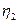> 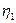неправильно.

Очевидно, независимо от того, работает манина 2 обратимо или необратимо, возможны только два случая:

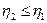(II,2)

Допустим, что машина 2 работает обратимо. В этом случае можно заставить обе машины обменяться ролями (машина 1 обратима по первоначальному условию). Повторив изложенное рассуждение, можно прийти к выводу, что:

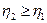
Очевидно, что этот вывод совместим с предыдущим лишь при условии, что единственное решение – это равенство, т.е. кпд двух машин:

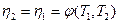, (II,3)

что и требовалось доказать.

Так как функция 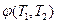не зависит от природы рабочего тела машины, то мы можем найти вид этой функции, используя любой частный случай, например такой, когда рабочим телом обратимого цикла Карно является идеальный газ.

Выражение (II,2) получено без каких-либо предположений относительно обратимости машины 2. Поэтому оно может относиться как как к обратимому, так и необратимому процессам. Из выражения (II,3) следует, что знак равенства относится к обратимым циклам. Следовательно, знак неравенства относится к необратимым циклам. В этих циклах необратимость связана, например, с тем, что часть работы путём трения превращается в теплоту, вследствие чего уменьшается кпд цикла.

Таким образом, кпд тепловой машины, работающей необратимо, меньше, чем кпд машины, работающей по обратимому циклу Карно между теми же температурами.

Полученные результаты относятся не только к циклу Карно. Они являются общими для любых циклических процессов. Это вытекает из положения, что любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, ограниченных бесконечно малыми отрезками изотерм и конечными отрезками адиабат.

Теперь докажем ещё одну теорему, необходимую для исследования цикла Карно.

Теорема Карно: коэффициент полезного действия цикла Карно больше коэффициента полезного действия любого цикла между теми же температурами.

Разобьём произвольный цикл abcd (рис.3) бесконечно большим количеством адиабат, а через отрезки цикла, заключенные между адиабатами, проведём изотермы. При этом получится бесконечно большое количество бесконечно малых циклов Карно. Очевидно, площадь любого из этих циклов отличается от площади, соответствующей элементарной части большого цикла, на бесконечно малую величину второго порядка, т.е. можно считать, что площадь всего цикла abcd совпадает с суммой площадей всех бесконечно малых циклов Карно.

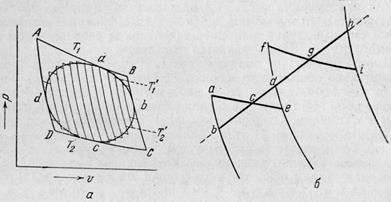
Рис.3. Произвольный цикл из бесконечно малых циклов Карно.

Из сказанного выше следует, что любой цикл можно заменить совокупностью бесконечно малых циклов Карно. Это, в свою очередь, означает, что теплота и работа произвольного цикла равны соответственно сумме теплот и сумме работ совокупности бесконечно малых циклов Карно.

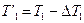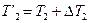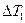Легко показать, что средний кпд произвольного цикла меньше кпд цикла Карно, протекающего между двумя крайними температурами Т₁ и Т₂ (цикл ABCD на рис.3). Действительно, каждый элементарный цикл Карно протекает между температурами Т’₁ и Т’₂ , причём и ( и 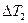больше нуля). Поэтому кпд элементарного цикла Карно

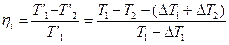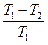< (II,4)

Средний коэффициент 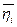любого цикла, очевидно, также меньше h цикла Карно между крайними температурами, что и требовалось доказать.

Так как кпд обратимого цикла Карно не зависит от природы рабочего вещества, то уравнение (II,4) относится к любым обратимым циклам Карно (знак равенства) и любым произвольным циклам с максимальной температурой Т₁ и минимальной температурой Т₂ (знак неравенства). Следовательно, выражение для кпд циклического процесса, записанное в виде

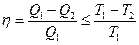(II,5)

(где Т₁ и Т₂ – максимальная и минимальная температуры теплообмена рабочего тела с источниками теплоты) является общим законом.

Из уравнения (II,5), определяющего коэффициент полезного действия, следует, что для обратимого цикла Карно:

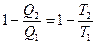или 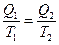(II,6)

Отношение 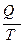(поглощённой системой теплоты к температуре) называется приведённой теплотой. Уравнение (II,6) показывает, что алгебраическая сумма приведённых теплот по обратимому циклу Карно равна нулю.

Для бесконечно малого обратимого цикла Карно, очевидно:

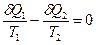(II,7)

где 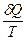- элементарная приведенная теплота.

Любой цикл может быть заменен совокупностью бесконечно малых циклов Карно, поэтому, складывая выражения (II,7) для всех бесконечно малых циклов, получаем для любого обратимого цикла:

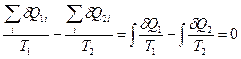(II,8)

Разность интегралов поглощенных ( 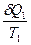) и выделенных ( 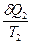) приведенных теплот является алгебраической суммой всех приведенных теплот по обратимому циклу:

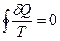(II,9)

Для необратимого цикла Карно, принимая во внимание уравнение (II,2), получаем:

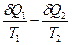< 0 (II,10)

и для любого необратимого цикла:

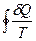< 0 (II,11)

Это - так называемое неравенство Клаузиуса.

Таким образом, сумма приведенных теплот (интеграл элементарных приведенных теплот) не зависит от пути процесса, а только от начального и конечного состояний. Следовательно, интеграл элементарных приведенных теплот в равновесном процессе равен приросту некоторой функции состояния системы:

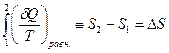(II,12)

а подынтегральное выражение есть дифференциал функции S:

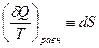(II,13)

Выражения (II,12) и (II,13) являются определениями функции S, которая называется энтропией.

Энтропия системы есть функция состояния системы; ее изменение равно сумме приведенных теплот, поглощенных системой в равновесном процессе. Энтропия является однозначной, непрерывной и конечной функцией состояния.

Как указывалось выше, элементарная теплота не является в общем случае дифференциалом функции. Из уравнения (II,13) видно, что δQ после деления на Т становится дифференциалом функции, т. е. с математической точки зрения, 1/Т является для теплоты интегрирующим множителем (или Т- интегрирующим делителем).

Если один из путей перехода системы в цикле неравновесный, а другой путь равновесный, т.е. круговой процесс в целом неравновесный, то, исходя из уравнения (II,11), получаем:

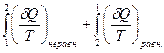< 0 (II,14)

Полученное выражение не означает, что в результате неравновесного кругового процесса изменяется энтропия системы. Энтропия системы как функция состояния принимает первоначальное значение, и ее изменение равно нулю. Сумма же приведенных теплот, полученных системой, меньше нуля, следовательно окружающая среда в результате цикла получает от системы некоторое количество приведенной теплоты. Если цикл прямой, то, следовательно, холодильник получает больше теплоты, чем в равновесном цикле для той же величины Q₁ и часть теплоты необратимо переходит от нагревателя к холодильнику.

Из уравнения (II,14) получаем:

< - =

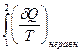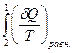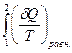
(для равновесного процесса допустима перестановка пределов с заменой знака на обратный).

Интеграл правой части уравнения может быть заменен в соответствии с уравнением (II,12) разностью энтропий:

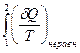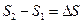< (II,15)

Соответствующее неравенство может быть записано в дифференциальной форме:

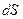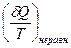
> (II,16)

Обобщая выражения (II,13) и (II,16), получаем:

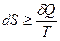. (II,17)

В том случае, когда отсутствует теплообмен между системой и окружающей средой ( 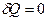), т. е. система является изолированной, уравнение (II,17) принимает вид:

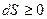
или в интегральной форме:

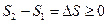
Таким образом, энтропия изолированной системы постоянна в равновесных процессах и возрастает в неравновесных. Это положение также справедливо для адиабатных процессов, при которых не происходит теплообмена с внешней средой. Иначе говоря, адиабатные равновесные процессы являются в то же время изоэнтропийными.

Исследуя энтропию, очевидно, можно предсказывать направление процесса. Если в изолированной системе для какого-либо процесса энтропия возрастает, то процесс возможен (положителен); если энтропия изолированной системы согласно расчету должна убывать, то процесс невозможен (отрицателен). При постоянстве энтропии процесс равновесный, т.е. система бесконечно близка к равновесию.

Следует подчеркнуть, что в системе, обменивающейся теплотой и работой с окружающей средой, возможны процессы, сопровождающиеся как возрастанием, так и убылью энтропии системы. Поэтому для однозначного решения вопроса о направлении процесса следует включить в систему все тела, участвующие в процессе, и, таким образом, сделать систему изолированной.

В изолированной системе процессы прекратятся, очевидно, тогда, когда энтропия системы достигнет максимального значения, возможного для данной системы при постоянстве некоторых ее параметров, а именно при постоянстве внутренней энергии U и объема V (условия изолированности системы). Дальнейшее изменение состояния системы должно было бы вызвать уменьшение энтропии, что в изолированной системе невозможно. Таким образом, признаком равновесия изолированной системы является максимальное значение энтропии при постоянных внутренней энергии и объеме системы (если нет других видов работы, кроме работы расширения). Следовательно, при равновесии должны соблюдаться условия:

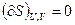и 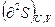< 0 (II,17а)

Очевидно, условие максимума рассматривается по отношению к энтропии, как функции каких-либо переменных (за исключением U и V,которые постоянны по условию). Такими переменными являются, например, давление пара над жидкостью, концентрации в растворе и др.

Законы термодинамики могут формулироваться по-разному. Одна из наиболее лаконичных формулировок первого и второго законов принадлежит Клаузиусу: