Методы расчета изменения энтропии

Уравнения (II, 12) и (II, 13), определяющие энтропию, являются единственными исходными уравнениями для термодинамического расчета изменения энтропии системы. Заменяя элементарную теплоту в уравнении (II, 13) ее выражениями через калорические коэффициенты (см. уравнения (I, 26) и (I, 32)), получаем для равновесных процессов:

dS = 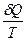= 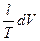+ 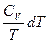(II, 18)

dS = 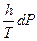+ 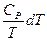(II, 19)

Уравнения (II, 18) и (II, 19) являются полными дифференциалами энтропии как функции переменных V, Т или P, Т. Коэффициенты этих уравнений – частные производные энтропии по соответствующим переменным.

Подставив в уравнение (II, 18) значения калорических коэффициентов для одного моля идеального газа: l = P = RT/V (уравнение (I, 37)) и h = –V = –RT/P (уравнение (I, 39)) и полагая С_V и С_P независимыми от температуры (что допустимо лишь в небольших температурных интервалах), получим после интегрирования в известных пределах:

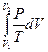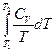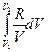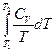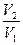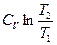
DS = + = + = R ln + (II,20)

DS = – 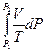+ 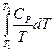= - 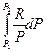+ 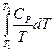= -R ln 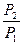+ C_P ln 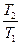(II,21)

Применим полученные выше соотношения для расчетов изменения энтропии при некоторых процессах:

1. Фазовые превращения (изотермические процессы; Т = const):

S₂ – S₁ = DS = 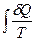= = 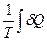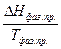(II, 22)

Так, например, теплота плавления бензола равна 9,764 кДж/моль; температура плавления t_пл. = 5,5°С (Т = 278,5 К). Следовательно, изменение энтропии 1 моль бензола при плавлении (энтропия плавления) равно:

DS_пл. = 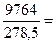35,06 Дж/моль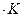

2. Нагревание при постоянном давлении (изобарный процесс; P = const). Из уравнений (I, 16) и(II, 13) получаем:

DS = 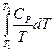(II, 23)

Найдем изменение энтропии одного моля алюминия при нагревании от 25 до 600°С. Истинная мольная теплоемкость алюминия может быть выражена уравнением:

С_р= 565,5 + 0,290 Т. По уравнению (II, 6) изменение энтропии будет равно:

DS = 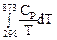= 565,5 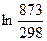+ 0,290(873 – 298) = 607,8 + 166,8 = 774,6 Дж/мольK

Смешение двух идеальных газов (изобарно-изотермический процесс). В смеси идеальных газов компоненты ведут себя независимо друг от друга, поэтому энтропия смеси идеальных газов является аддитивной функцией состава.

При смешении двух газов в количестве 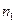и 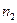при постоянных температуре и давлении после удаления разделяющей их перегородки каждый газ изменяет свой объем от первоначального до объема смеси, равного сумме исходных объемов ( 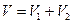). Изменение энтропии при смешении является суммой изменения энтропии каждого газа при его изотермическом расширении. Принимая во внимание уравнение (II, 4), это изменение равно:

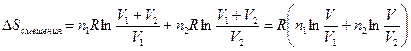(II,24)

Гиббс в свое время обратил внимание на некоторую странность полученного результата. Если два газа идентичны, то состояния газов до и после удаления перегородки неотличимы. Следовательно, изменения энтропии системы после удаления перегородки не происходит, потому что начальное и конечное состояния одинаковы. Но для двух нетождественных газов, сколь бы малым ни было различие между ними, изменение энтропии системы при смешении определяется соотношением (II,24). Обычно, в большинстве физических систем, малое изменение одной величины приводит к малому изменению другой зависимой величины. Иначе обстоит дело с энтропией смешения. Даже совершенно незначительное различие между двумя газами приводит к изменению энтропии. Если газы идентичны, то 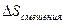скачком падает до нуля. Такое скачкообразное поведение энтропии смешения называют парадоксом Гиббса.

Постулат Планка.

По уравнению (II, 3) невозможно вычислить абсолютное значение энтропии системы. Такую возможность дает новое, недоказуемое положение, не вытекающее из двух законов термодинамики, которое было сформулировано М.Планком (1912). Согласно этому положению, называемому постулатом Планка, энтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю:

S₀ = 0

Строго говоря, постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены (в кристаллической решетке все узлы заняты молекулами или атомами, правильно чередующимися и закономерно ориентированными). Такие кристаллы называются идеальными твердыми телами. Реальные кристаллы не являются таковыми, так как их кристаллическая решетка построена не идеально.

Энтропия кристаллической решетки, построенной в некоторой степени беспорядочно, больше энтропии идеально построенной кристаллической решётки. Поэтому реальные кристаллы и при 0 К обладают энтропией, большей нуля. Однако энтропии реальных хорошо образованных кристаллов индивидуальных веществ при абсолютном нуле невелики.

В соответствии с постулатом Планка уравнение (II, 23) для идеального твёрдого тела примет вид:

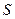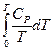= (II, 25)

Постулат Планка используется при термодинамическом исследовании химических процессов для вычисления абсолютных значений энтропии химических соединений – величин, которые имеют большое значение при расчете химических равновесий.

Энтропия широко используется в технической термодинамике (теплотехнике), как один из важных параметров рабочего тела в тепловой машине, например, водяного пара. Величины энтропии водяного пара в данном состоянии вычисляются по сравнению с некоторым стандартным состоянием. Эти значения энтропии используются для построения так называемых энтропийных диаграмм состояния водяного пара в координатах S-Т или S-H (диаграмма Молье). В таких диаграммах подобно диаграммам V-P можно изображать различные процессы, протекающие в рабочем теле тепловой машины и составляющие рабочие циклы машины.