Статистическая интерпретация энтропии.
В основу понятия энтропии как функции состояния положена макроскопическая концепция. Справедливость второго закона термодинамики связана с реальностью необратимых процессов. В отличие от необратимых макроскопических процессов, которые мы наблюдаем вокруг, законы классической и квантовой механики симметричны во времени, т.е. согласно законам механики система, которая может эволюционировать из состояния 1 в состояние 2, точно так же может эволюционировать из состояния 2 в состояние 1. Например, спонтанный поток молекул газа из одной части сосуда, где газ имеет бóльшую плотность, в другую часть сосуда, где газ имеет меньшую плотность, и обратный поток совершенно согласуются с законами механики. Но такой обратный поток противоречит второму закону термодинамики. Процессы, которые второе начало термодинамики отвергает как невозможные, не нарушают законов механики. В то же время все необратимые макроскопические процессы, такие, как теплообмен, происходят вследствие движения атомов и молекул, которое в свою очередь подчиняется законам механики; теплообмен обусловлен межмолекулярными столкновениями, при которых происходит передача энергии.
Каким образом необратимые процессы возникают из обратимого движения молекул?
Чтобы примирить обратимость механики с необратимостью термодинамики, Л.Больцман предложил следующее соотношение между микроскопическими состояниями и энтропией:
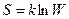 (II,32)
(II,32)
где W – число микросостояний, соответствующих тому макросостоянию, энтропия которого равна S. Постоянная k, введенная Больцманом, называется теперь постоянной Больцмана.
Следующий пример объясняет физический смысл W. Рассмотрим макросистему – некоторый ящик с газом. Пусть в одной части ящика находится 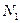 молекул этого газа, а в другой -
молекул этого газа, а в другой - 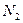 молекул. Каждая молекула газа может находиться как в одной, так и в другой части ящика. Общее число способов, которыми
молекул. Каждая молекула газа может находиться как в одной, так и в другой части ящика. Общее число способов, которыми 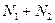 молекул можно распределить между частями ящика так, чтобы в одной части оказалось
молекул можно распределить между частями ящика так, чтобы в одной части оказалось 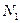 молекул, а в другой
молекул, а в другой 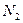 молекул, равно W. Число различных микросостояний с
молекул, равно W. Число различных микросостояний с 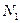 молекулами в одной части ящика и
молекулами в одной части ящика и 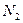 молекулами в другой составляет
молекулами в другой составляет
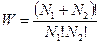
По Больцману, чем больше W, тем вероятнее, что это макросистема, т.е. система, которая подчиняется статистическим законам. Таким образом, необратимые процессы, происходящие с увеличением энтропии, соответствуют эволюции к наиболее вероятным состояниям. Равновесные состояния отличаются тем, что W в этих состояниях достигает максимума, т.е. они являются наиболее вероятными.
Можно показать, что в приведенном выше примере наиболее вероятным состоянием (W достигает максимального значения) является то, при котором 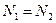 .
.

Дата добавления: 2015-05-21; просмотров: 851;
