Энергия Гиббса

Желая учесть в общей форме другие виды работы, кроме работы расширения, представим элементарную работу как сумму работы расширения и других видов работы:

dW = PdV + dW' (III, 14)

где dW' – сумма элементарных работ всех видов, кроме работы расширения. Мы назовем эту величину элементарной полезной работой, а величину W' – полезной работой. Из уравнений (III, 11) и (III, 1) получаем:

dW' £ TdS – dU – PdV (III, 15)

Отсюда можно найти величину W', получаемую при переходе системы из состояния 1 в состояние 2, интегрируя это уравнение в соответствующих пределах при постоянных температуре и давлении:

Сгруппировав все величины, относящиеся к одному состоянию, получим:

W' £ – (U₂ – TS₂ + PV₂) + (U₁ – TS₁+ PV₁)(III, 16)

Обозначим через G выражения, стоящие в скобках правой части уравнения, которые являются функциями состояния, т. е.

G º U + PV – TS º H – TS (III, 17)

Тогда уравнение (III, 16) можно записать следующим образом:

W' £ – G₂ + G₁ = – ( G₂ – G₁ ) = – DG (III, 18)

Так как DG не зависит от пути процесса, то, при условии постоянства P и Т, для равновесных процессов W' будет максимально:

W'_макс. = – G₂ + G₁ = – (G₂ – G₁) = – DG (III, 19)

где G – функция состояния, определяемая равенством (III, 17) и называемая энергией Гиббса. Таким образом, максимальная полезная работа при изобарно-изотермических процессах равна убыли энергии Гиббса.

Для получения полного дифференциала функции G при переменных P и Т дифференцируем уравнение (III, 17):

dG = dU – Т dS – SdT + PdV + VdP

Так как

dU £ TdS – PdV – dW',то

dG £ -SdT + VdP – dW' (III, 20)

Из этого уравнения при постоянных Т и P получаем уравнение (III, 18) в дифференциальной форме.

При отсутствии всех видов работы, кроме работы расширения (dW' = 0), в общем случае:

dG £ -SdT + VdP (III, 21)

а для равновесных процессов

dG = -SdT + VdP (III, 22)

Полагая T = const и P = const, а также при условии отсутствия всех видов работы, кроме работы расширения (dW’ = 0), получаем из уравнения (III, 21):

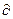( G) _T,Р £ 0 (III, 22а)

Энергия Гиббса системы при постоянных давлении и температуре уменьшается при неравновесных (самопроизвольных) процессах, при равновесии её значение остаётся постоянным. Очевидно, равновесное состояние системы при данных P и Т соответствует минимуму энергии Гиббса.