Соотношения Максвелла.

Рассмотрим теперь вторые смешанные производные характеристических функций. Принимая во внимание уравнения (III, 23а) - (III, 26а), можем записать:

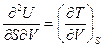(III, 27)и

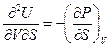(III, 28)

Значение смешанных производных непрерывной функции не зависит от порядка дифференцирования, поэтому, если в уравнениях (III, 27)и(III, 28)равны левые части уравнений, то равны и их правые части:

=

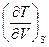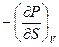
Справедливость полученного уравнения не изменится, если его «перевернуть», т.е. представить в следующем виде:

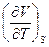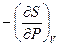= (III, 29)

Полученное уравнение (III, 29) принадлежит к числу так называемых соотношений Максвелла.Совершенно аналогично можно получить три других соотношения:

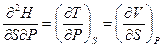или

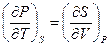(III, 30)

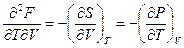или

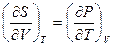(III, 31)

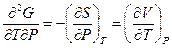или

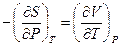(III, 32)

Эти соотношения позволяют при необходимости переходить от одних частных производных к другим, заменяя частные производные, которые не могут быть непосредственно определены на опыте (производные энтропии по параметрам Р и V) на величины, которые заведомо легче связать с экспериментом (производные давления или объема по температуре и другие). Поэтому роль соотношений Максвелла, особенно

(III, 31)и(III, 32),в термодинамике чрезвычайно велика.

Приведем только один пример. Из объединенного первого и второго законов термодинамики следует:

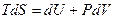
Если разделить обе части последнего уравнения на 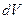, считая температуру Т постоянной, получим:

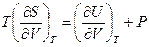
Заменяя теперь 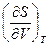из третьего соотношения Максвелла (смотри (III, 31))на 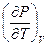, после простых преобразований получим:

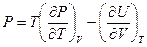(III, 33)

Для одного моля идеального газа 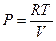. Подставляя это выражение в левую и правую части уравнения (III, 33)и считая объем постоянным, после дифференцирования будем иметь:

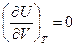
Полученный результат означает независимость внутренней энергии идеального газа от объема (и давления) при постоянной температуре. Это положение, принятое нами на основании опыта Гей-Люссака – Джоуля (смотри стр.15), после приведенного вывода непосредственно вытекает из самого уравнения состояния идеального газа и законов термодинамики.