Энергия Гиббса смеси идеальных газов. Химический потенциал.

Допустим, что равновесная газовая смесь содержит i индивидуальных веществ.

Из определения энергии Гиббса (III, 17) следует:

G = U + PV – TS

Рассмотрим в этом выражении каждое слагаемое.

Согласно уравнению (I, 25а) зависимость внутренней энергии 1 моль индивидуального i-ого вещества от температуры представляется следующим образом:

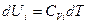(III, 37)

где 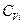- молярная теплоёмкость при постоянном объёме i-ого газа. Так как для идеального газа теплоёмкость 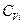не зависит от температуры, интегрируя при этом условии уравнение () от нуля до Т, получим:

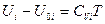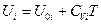или (III, 38)

где 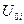- внутренняя энергия 1 моль i-ого вещества при 0 К. Если в смеси этого вещества содержится моль, то умножая обе части уравнения (III, 38) на и суммируя по всем индивидуальным веществам системы, будем иметь:

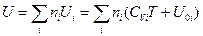(III, 39)

Второе слагаемое в выражении для энергии Гиббса, исходя из уравнения Менделеева – Клапейрона, запишем в виде:

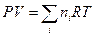(III, 40)

Рассмотрим третье слагаемое. Из уравнения (II, 21) для 1 моль идеального газа следует:

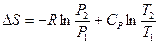
Положим 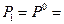1 атм и 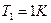, тогда

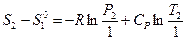или 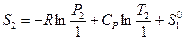(III, 41),

где 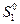- стандартная (так как относится к 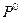= 1 атм.) энтропия 1 моль идеального газа при 1 К, которая также называется энтропийной постоянной идеального газа. Индекс «2» теперь можно отбросить и выражение запишется в виде:

,

где 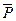- относительное давление. Стоящие под знаком логарифма величины 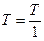и 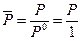- безразмерные. Следует отметить, что величины 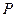и 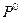могут быть выражены в любых, но обязательно одних и тех же единицах – атмосферах, паскалях, миллиметрах ртутного столба и т.д. Однако, выражение давления в атмосферах имеет очевидное преимущество, т.к. в этом случае давление и относительное давление численно совпадают .

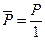Таким образом, для 1 моля i-ого компонента газовой смеси мы можем записать:

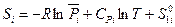(III, 42),

где 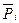- относительное парциальное давление i-ого компонента.

Умножая обе части выражения (III, 42) на и суммируя по всем индивидуальным веществам в системе, получим:

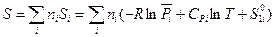(III, 43)

Подставив значения U, PV и S из уравнений (III, 39), (III, 40) и (III, 43) в выражение для энергии Гиббса, находим следующее выражение:

(III, 44)

Первые пять слагаемых в этом уравнении зависят от природы индивидуального i-ого вещества и температуры, но не зависят от состава смеси и давления. Алгебраическую сумму этих пяти слагаемых, стоящих в скобках, обозначим через 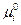. Тогда

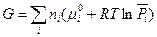(III, 45)

или, если ввести обозначение

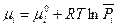(III, 46)

то выражение (III, 45) можно окончательно представить в таком виде:

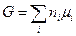(III, 47)

Величина 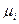называется химическим потенциалом индивидуального i-ого вещества, а величина 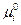- стандартным химическим потенциалом (при 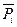=1).

Так как для идеальной газовой смеси и 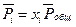, то уравнение

(III, 46) можно привести к виду:

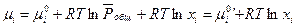(III, 48),

где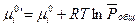

Если 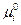есть функция только температуры, то 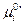зависит не только от температуры, но и давления.

Подставив значения 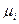из уравнений (III, 46) и (III, 48) в (III, 47), то соответственно получим:

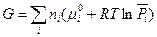(III, 49)

и

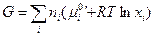(III, 50)

Чтобы прояснить смысл понятия «химический потенциал», продифференцируем выражение (III, 49) как произведение при постоянных Р и Т:

(III, 51)

Легко показать, что при постоянных Р и Т второе слагаемое 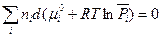(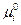зависит только от температуры).

Тогда для системы переменного состава

(III, 52)

Примем постоянным число молей всех компонентов смеси, кроме i-ого компонента, тогда

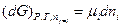(III, 53)

или

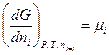(III, 54)

Из определения химического потенциала как частной производной вытекает следующее. Если при постоянных температуре Т и давлении Р к бесконечно большому количеству смеси (раствора) определенного состава добавить один моль какого-нибудь компонента, то химический потенциал будет равен приросту энергии Гиббса.

Сказанное выше позволяет определить химический потенциал как энергию Гиббса, приходящуюся на один моль компонента в смеси или, иными словами, парциальную молярную энергию Гиббса.

Полный дифференциал энергии Гиббса в соответствии с (III, 26) и (III, 53) запишется следующим образом:

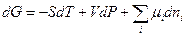(III, 55)

Исходя из этого выражения, можно показать, что для систем с переменным составом фундаментальные термодинамические уравнения будут иметь следующий вид:

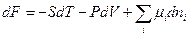(III, 56)

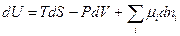(III, 57)

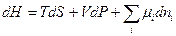(III, 58)

Из уравнений (III, 55) – (III, 58) вытекает:

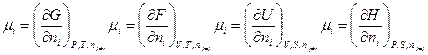
Таким образом, химический потенциал является частной производной по количеству i-ого компонента от любой характеристической функции G,F,U и H при постоянном количестве остальных индивидуальных веществ в системе и постоянстве соответствующих независимых переменных.

Необходимо отметить, что химический потенциал является интенсивным свойством системы.

Химический потенциал для одного моля чистого вещества в состоянии идеального газа при любых температуре Т и давлении Р можно рассчитать по уравнению:

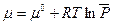(III, 59)

Вообще химический потенциал чистого вещества – это его мольная энергия Гиббса: 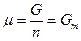, где 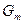- энергия Гиббса 1 моля чистого вещества.

Для практических целей широко используют мольную энергию Гиббса в стандартном состоянии (при 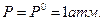и Т = 298К).

В этом случае

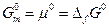
Величину, которую мы обозначили 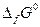, также определяют как стандартную молярную энергию Гиббса образования одного моля вещества из простых веществ, находящихся в их стандартных состояниях.

При этом полагают, что энергия Гиббса образования ( 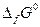) всех элементов при всех температурах равна нулю.

Стандартные энергии Гиббса образования многих соединений табулированы. По взятым из таблиц значениям 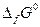может быть рассчитано изменение энергии Гиббса химической реакции аналогично тому, как рассчитывается тепловой эффект химической реакции по значениям стандартных теплот образования веществ, участвующих в химической реакции.