В отсутствие помех
Рассмотрим вопросы, связанные с передачей информации встатических знаковых («дискретных») информационных системах,на примере функционирования системы передачи дискретных сообщений типа «ДИС–кодер–посто-янное запоминающее устройство (ПЗУ)–сканер–линия связи–декодер–ПИ» (см. рис. 4). Для конкретности будем подразумевать под такой системой электронную почту. Пользователь персонального компьютера с помощью клавиатуры ПК набирает текст, который кодируется и помещается в ПЗУ. По команде пользователя текст отправляется по кабелю на сервер (ПЗУ). Адресат-ПИ обращается в свой «почтовый ящик», анализирует почту и нужные письма сканирует. По линии связи они поступают на ПК адресата и декодируются. Фактор времени как таковой здесь отсутствует; поэтому такую систему можно считать статической.

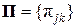
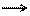

 U = { uj }
U = { uj }  u1 ○ π11 = 1 ○ w1 W = {wk}
u1 ○ π11 = 1 ○ w1 W = {wk} 

 P = { Pj }
P = { Pj }  u2 ○ ○ w2 Pвых = {P'k}
u2 ○ ○ w2 Pвых = {P'k} 
I = { Ij }  uj ○ ○ wk Iвых ={I'k j; i, k = 1, 2, …, N }
uj ○ ○ wk Iвых ={I'k j; i, k = 1, 2, …, N }
H(U) = – 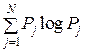 uN ○ πN1 = 1 π2N = 1 ○ wN
uN ○ πN1 = 1 π2N = 1 ○ wN
Рис. 4. Статическая система передачи
знаковой (дискретной) информации без помех
Пусть источник ДИС выдаёт некоторое сложное знаковое сообщение (текст) Si(n) = ( ui1, ui2, …, uil, …, uin ), которое посредством входного преобразователя (на рис. 4 не показан) записывается с помощью некоторого множества символов 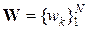 в ПЗУ. Через некоторое время (по запросу получателя информации ПИ или по расписанию) сканер считывает из ПЗУ это сообщение, это сообщение передаётся по линии связи, декодируется и посредством выходного преобразователя (на рис. 4 не показан) предоставляется получателю ПИ в виде последовательности символов S'i(n) = (wi1, wi2, …, wil, …, win). Функционирующую таким образом информационную систему будем называть статической системой передачи информации (ССПИ).
в ПЗУ. Через некоторое время (по запросу получателя информации ПИ или по расписанию) сканер считывает из ПЗУ это сообщение, это сообщение передаётся по линии связи, декодируется и посредством выходного преобразователя (на рис. 4 не показан) предоставляется получателю ПИ в виде последовательности символов S'i(n) = (wi1, wi2, …, wil, …, win). Функционирующую таким образом информационную систему будем называть статической системой передачи информации (ССПИ).
Знаки {uj}  и символы {wk}
и символы {wk}  могут иметьразличную физическую реализацию. Например, знакам {uj}
могут иметьразличную физическую реализацию. Например, знакам {uj}  могут соответствовать клавиши латинизированной клавиатуры компьютера, а символам {wk}
могут соответствовать клавиши латинизированной клавиатуры компьютера, а символам {wk}  – изображения на мониторе
– изображения на мониторе
компьютера фигурки моряка-сигнальщика с соответствующими положениями рук и флажков (морской тренажёр для обучения семафорной азбуки). Или же: знакам {uj}  могут соответствовать фонемы обычной речи, а символам {wk}
могут соответствовать фонемы обычной речи, а символам {wk}  – буквы алфавита данного языка (анализатор речи). Или же: знакам {uj}
– буквы алфавита данного языка (анализатор речи). Или же: знакам {uj}  могут соответствовать фонемы, а символам {wk}
могут соответствовать фонемы, а символам {wk}  – визуальные знаки азбуки глухонемых и т. п.
– визуальные знаки азбуки глухонемых и т. п.
В последнем случае анализатор речи записывает поступившее от микрофона сообщение, распознаёт фонемы {uj}  и записывает речевое сообщение в ПЗУ с помощью символов {wk}
и записывает речевое сообщение в ПЗУ с помощью символов {wk}  , обозначающих буквы данного языка. При считывании информации символы {wk}
, обозначающих буквы данного языка. При считывании информации символы {wk}  превращаются в знаки азбуки глухонемых, которые и отображаются на дисплее монитора. При этом количество фонем {uj}
превращаются в знаки азбуки глухонемых, которые и отображаются на дисплее монитора. При этом количество фонем {uj}  в сообщении (фразе) Si(n) = ( ui1, ui2, …, uil, …, uin ) может не совпадать с количеством символов {wk}
в сообщении (фразе) Si(n) = ( ui1, ui2, …, uil, …, uin ) может не совпадать с количеством символов {wk}  , что может привести к потере информации в системе ССПИ. Например, в слове «солнце» пять фонем из множества {uj}
, что может привести к потере информации в системе ССПИ. Например, в слове «солнце» пять фонем из множества {uj}  : с-о-н-ц-е. Однако оно записывается с помощью шести символов {wk}
: с-о-н-ц-е. Однако оно записывается с помощью шести символов {wk}  : с-о-л-н-ц-е. В силу смысловой избыточности русского языка в этом случае потери информации в системе ССПИ не произойдёт. С другой стороны, очень часто из русского языка пытаются «изгнать» букву «ё». Поэтому синтезатор речи вместо слова «съём» (квартиры) синтезирует слово «съем», вместо «вёдро» (о погоде) – «ведрó», вместо «осёл» – «осéл» и т. п. Или: как правильно запрограммировать синтезатор, если в тексте есть фразы «все равно» и «все равны»? Как нужно понимать первую фразу: то ли как «всё равно», то ли считать, что в ней допущена ошибка и её следует синтезировать как «все равны»?
: с-о-л-н-ц-е. В силу смысловой избыточности русского языка в этом случае потери информации в системе ССПИ не произойдёт. С другой стороны, очень часто из русского языка пытаются «изгнать» букву «ё». Поэтому синтезатор речи вместо слова «съём» (квартиры) синтезирует слово «съем», вместо «вёдро» (о погоде) – «ведрó», вместо «осёл» – «осéл» и т. п. Или: как правильно запрограммировать синтезатор, если в тексте есть фразы «все равно» и «все равны»? Как нужно понимать первую фразу: то ли как «всё равно», то ли считать, что в ней допущена ошибка и её следует синтезировать как «все равны»?
Значит, даже в отсутствие помех в канале КПДС при работе системы ССПИ может происходить потеря синтактической («перепутывание знаков»), а значит и семантической информации.
Как можно оценить потери информации в таких системах ССПИматематически? Для простоты будем считать, что количество знаков {uj} на входе канала КПДС и символов {wk} на его выходе одно и то же – N (вообще говоря – это не обязательно!).
В разд. 3 мы установили, что простейший источник ДИС можно характеризовать тремя множествами: множеством первичных знаков U = {uj}  , множеством вероятностей P = {Pj}
, множеством вероятностей P = {Pj}  независимого появления знаков uj в произвольной последовательности Si(n) (Pj = P(uj) – априорные, по отношению к каналу КПДС, вероятности) и информационным множеством I = {Ij}
независимого появления знаков uj в произвольной последовательности Si(n) (Pj = P(uj) – априорные, по отношению к каналу КПДС, вероятности) и информационным множеством I = {Ij}  ; Ij = – log Pj.
; Ij = – log Pj.
На выходе канала КПДС могут появляться любые символы wk из множества W = {wk}  . Вероятности их появления P'k (вообще говоря, P'k ≠ Pj) образуют множество выходных вероятностей Pвых = {P'k}
. Вероятности их появления P'k (вообще говоря, P'k ≠ Pj) образуют множество выходных вероятностей Pвых = {P'k}  . Каждый из символов wk
. Каждый из символов wk 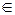 W может нести некоторое количество информации Ik j, (k, j = 1, 2, …, N ), содержащейся во входных элементарных сообщениях (знаках) uj
W может нести некоторое количество информации Ik j, (k, j = 1, 2, …, N ), содержащейся во входных элементарных сообщениях (знаках) uj 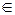 U. Каждому символу wk
U. Каждому символу wk 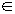 W по определённому правилу ( распознавания символов) ставится в соответствие один, и только один из знаков uj
W по определённому правилу ( распознавания символов) ставится в соответствие один, и только один из знаков uj 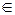 U (символу wk присваивается значение знака uj ). Субъект-ПИ знает это правило и соответствующим образом воспринимает полученное сообщение.
U (символу wk присваивается значение знака uj ). Субъект-ПИ знает это правило и соответствующим образом воспринимает полученное сообщение.
Поскольку количество знаков {uj}  и символов {wk}
и символов {wk}  одинаково и равно N, то канал КПДС можно охарактеризовать квадратной матрицей соответствия Π = || πjk; j, k = 1, 2, …, N || порядка N, в каждой строке которой стоит одна единица и (N – 1) нолей. Если записать алфавит {uj}
одинаково и равно N, то канал КПДС можно охарактеризовать квадратной матрицей соответствия Π = || πjk; j, k = 1, 2, …, N || порядка N, в каждой строке которой стоит одна единица и (N – 1) нолей. Если записать алфавит {uj}  в виде вектора-строки uТ = || u1, u2, …, uj, …, uN || и аналогично совокупность {wk}
в виде вектора-строки uТ = || u1, u2, …, uj, …, uN || и аналогично совокупность {wk}  выходных символов в виде wТ = ||w1, w2, …, wk, …, uN ||, то функционирование системы ССПИ математически может быть представлено как uТ Π = wТ, или w = ΠТ u. При этом сообщению (uj + ul) соответствует событие uj U ul.
выходных символов в виде wТ = ||w1, w2, …, wk, …, uN ||, то функционирование системы ССПИ математически может быть представлено как uТ Π = wТ, или w = ΠТ u. При этом сообщению (uj + ul) соответствует событие uj U ul.
Если матрица Π – диагональная (Π = || δjk; j, k = 1, 2, …, N ||, где δjk – символ Кронекера: δjk = 1 при j = k и δjk = 0 при j ≠ k), то каждому знаку uj будет соответствовать один, и только один символ wj – и никакой потери синтактической информации в канале КПДС происходить не будет, поскольку в этом случае по формуле полной вероятности 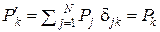 , и в этом случае выход канала КПДС являетсявторичным источником ДИСс характеристиками:
, и в этом случае выход канала КПДС являетсявторичным источником ДИСс характеристиками:
P'k = Pk, P'j = Pj, Ik j = – δjk log Pk = – δk j log Pj = – log Pk = Ik = Ij.
Удельная информативность  (U, П) такого вторичного источника равна удельной информативности первичного источника ДИС:
(U, П) такого вторичного источника равна удельной информативности первичного источника ДИС:
 (U, П) =
(U, П) = 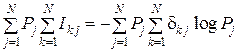 ,
,
или  (U, П) =
(U, П) = 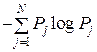 = H(U) (бит/знак). (6.1)
= H(U) (бит/знак). (6.1)
Если матрица Π – диагонализируемая, то есть если она может быть приведена, за счёт перестановки столбцов, к диагональному виду, то потери информации в канале КПДС с матрицей соответствия П происходить также не будет. Просто каждому wk (k = 1, 2, …, N ) будет присваиваться значение одного, и только одного знака uj в соответствии со структурой матрицы П.
Например, матрица соответствия П= 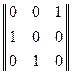 – диагонализируемая, и на выходе канала КПДС символу w1 будет присваиваться значение знака u2,
– диагонализируемая, и на выходе канала КПДС символу w1 будет присваиваться значение знака u2,
w2 → u3 и w3 → u1.
А вот матрица П= 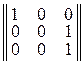 – не диагонализируема, и на выходе соответствующего матрице П канала КПДС символу w1 будет присваиваться значе-
– не диагонализируема, и на выходе соответствующего матрице П канала КПДС символу w1 будет присваиваться значе-
ние знака u1 – с вероятностью P1, символу w3: значение u2 – с вероятностью P2 и значение u3 с вероятностью P3, а символ w3 на выходе КПДС не появится никогда. Поэтому в таком канале КПДС будет происходить частичная потеря информации относительно информации источника ДИС.
Можно ли узнать заранее, по виду матрица П, диагонализируема она или же нет? И если нет, то, какое количество синтактической информации теряется в канале КПДС при данном источнике ДИС? И у какого из источников ДИС потери информации будут наименьшими?
На первый вопрос можно ответить, просмотрев все столбцы матрицы П. На ЦВМ это можно сделать автоматически. У диагональной матрицы Π = || δjk; j, k = 1, 2, …, N || определитель (детерминант) равен единице: det Π = 1. Поскольку для любой квадратной матрицы A перестановка столбцов (или строк) не приводит к изменению модуля её детерминанта, то матрица Π будет диагонализируемой, если | det Π | = 1.
Если det Π = 0, то матрица Π – не диагонализируема, и в соответствующем ей канале КПДС будет происходить потеря информации. В таком случае нам нужно знать, какой процент потерь информации произойдёт в канале КПДС в среднем на один знак данного источника ДИС (то есть информационную надёжность данной системы ССПИ ).
Ясно, что если при данных значениях j и k символу wk приписывается значение знака uj (то есть πjk = 1) и это соответствие одно-однозначное (то есть иных значений у символа wk не бывает), то P(wk) = P(uj), или P'k = Pj, и количество информации Ik j, содержащейся в символе wk относительно знака uj, равно
Ik j = – log Pj = log (π j k /P'k).
Если πjk = 0, то будем считать, что количество информации Ik j, содержа-
щейся в символе wk относительно знака uj, равно нулю, поскольку в среднем
π j k log (π j k /P'k) = 0.
Если же π j k = 1 и P'k ≠ Pj, то по формуле полной вероятности
P'k ≡ P(wk) = 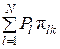 =
= 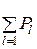 > Pj,
> Pj,
где в суммировании по индексу l участвуют только те из величин πjk столбца k
матрицы соответствия Π, значения которых равны единице.
Поскольку все значения Pl (как вероятности) в сумме 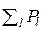 – положительны, то 0 < Pl < (P'k =
– положительны, то 0 < Pl < (P'k = 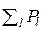 ) < 1.
) < 1.
Значит, в этом случае выполняется строгое неравенство
0 < 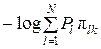 < – log Pj < ∞,
< – log Pj < ∞,
или 0 < Ik j < Ij < ∞, то есть в символе wk, соответствующему условию π jk = 1 и P'k ≠ Pj, содержится меньшее количество информации, чем в знаке uj.
Таким образом,
в качестве меры количества информации,
которая содержится в выходном символе wk
относительно входного знака uj источника ДИС U = {uj}  на выходе статического канала КПДС с матрицей соответствия Π
можно полагать величину Ik j = π j k log (π j k /P'k), где P'k =
на выходе статического канала КПДС с матрицей соответствия Π
можно полагать величину Ik j = π j k log (π j k /P'k), где P'k = 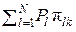 . .
|
Среднее количество информации, содержащейся в совокупности W всех выходных символов wk (k = 1, 2, …, N ) относительно некоторого входного зна-
ка uj, есть
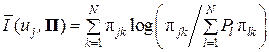 .
.
Среднее количество информации, которое получает субъект-ПИ на выходе канала КПДС системы ССПИ, приходящейся на любой из знаков uj 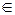 U ис-
U ис-
точника ДИС:
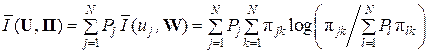 (бит/знак). (6.2)
(бит/знак). (6.2)
Безразмерный коэффициент информационной надёжности системы ССПИ 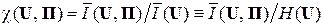 зависит как от информационных характеристик входного источника ДИС {U, P, I, S}, так и от характеристик канала КПДС {W, Π}.
зависит как от информационных характеристик входного источника ДИС {U, P, I, S}, так и от характеристик канала КПДС {W, Π}.
Можно поставить вопрос: каково же максимальное по всевозможным источникам ДИС значение коэффициента надёжности 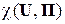 ? Это значение можно назвать коэффициентом надёжности
? Это значение можно назвать коэффициентом надёжности 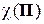 данного канала КПДС, поскольку он определяется только структурой матрицы соответствия Π.
данного канала КПДС, поскольку он определяется только структурой матрицы соответствия Π.
Для ответа на поставленный вопрос заметим, что формула (6.2) определяет среднее количество информации, получаемое на выходе канала КПДС при подключении на его вход данного источника ДИС U, которое приходится на один знак из совокупности U= {uj}  . Значит, соответствующими численными методами линейного программирования можно найти такой источник ДИС (то есть имеющий такие значения P1, P2, …, Pj, …, PN при условии
. Значит, соответствующими численными методами линейного программирования можно найти такой источник ДИС (то есть имеющий такие значения P1, P2, …, Pj, …, PN при условии 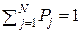 ), который реализует максимальное значение величины
), который реализует максимальное значение величины 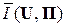 . Мы не будем входить в детали решения такой задачи, а проиллюстрируем вычисление коэффициента надёжности
. Мы не будем входить в детали решения такой задачи, а проиллюстрируем вычисление коэффициента надёжности 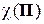 на простейшем примере.
на простейшем примере.
Рассчитаем среднее количество информации 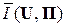 на выходе системы ССПИ, имеющей в качестве источника ДИС совокупность характеристик
на выходе системы ССПИ, имеющей в качестве источника ДИС совокупность характеристик
U = {u1, u2, u3}; P = {1/3, 1/3, 1/3}; I = {log 3, log 3, log 3};
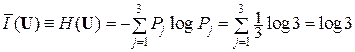 ≈ 1,6 (бит/знак),
≈ 1,6 (бит/знак),
а в качестве канала КПДС – канал с недиагонализируемой матрицей соответствия (см. предыдущие примеры) П= 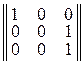 .
.
В этом случае: P'1 = P1 = 1/3, P'2 = 0, P'3 = 1/3 + 1/3 = 2/3, и с вероятностью P1 = 1/3 мы будем получать соответствие символа w1 знаку u1, то есть I11 = log 3; с вероятностью P2 = 1/3 – соответствие символа w3 знаку u2, то есть I32 = log (3/2), и с вероятностью P3 = 1/3 – значение u3, то есть I33 = log (3/2).
Среднее на один знак алфавита U количество информации на выходе системы ССПИ есть: 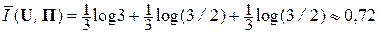 (бит/знак), то есть потери информации в такой системе составляют около 0,87 бит-на-знак алфавита U, акоэффициент информационной надёжностиχ(U, П) ≈ 0,45.
(бит/знак), то есть потери информации в такой системе составляют около 0,87 бит-на-знак алфавита U, акоэффициент информационной надёжностиχ(U, П) ≈ 0,45.
Значит, в рассмотренном канале КПДС теряется около 55 % информации.
Если же к каналу КПДС подключить источник ДИС с характеристиками
P = { 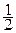 ,
, 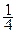 ,
, 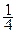 }, I = {1, 2, 2},
}, I = {1, 2, 2}, 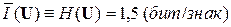 ,
,
то этот источник можно закодировать с помощью множества промежуточных символов V = {v1, v2} таким образом (алгоритм Шеннона-Фано):
u1 → v1; u2 → (v2, v1); u3 → (v2, v2).
Если подавать эти равновероятные символы v1 и v2 в канал КПДС с матрицей соответствия Π рассмотренной нами системы ССПИ, то получим следующее: символу w1 с вероятностью 0,5 будет присваиваться значение промежуточного символа v1, а символу w3 с вероятностью 0,5 значение v3. В такой системе ССПИ потерь синтактической информации не будет, источник ДИС за счёт соответствующего кодера будет согласован с каналом КПДС, имеющим данную матрицу соответствия Π, а канал КПДС может обслуживать различные источники ДИС U = {u1, u2, u3}, у которых алфавит содержит только три первичных знака и обладает удельной информативностью не более 1,5 бит/знак.
Практически более интересно рассмотреть такие каналы КПДС с диагонализируемыми матрицами соответствия Π, в которых потери информации происходят не за счёт «неправильного» построения алгоритма распознавания знаков uj, а за счёт различных помех, которые воздействуют на канал КПДС системы ССПИ. Этот вопрос мы рассмотрим в разд. 7.
Вопросы для самопроверки
1. Какова общая структура и математическая модель статической системы передачи дискретных сообщений?
2. Что такое матрица соответствия и что она характеризует?
3. Что такое диагонализируемая матрица соответствия и каков её смысл?
4. Как проверить диагонализируемость матрицы соответствия?
5. Как определить среднее количество информации на выходе системы передачи дискретных сообщений, обладающей известной матрицей соответствия, и коэффициент её информационной надёжности в отсутствие помех?
Дата добавления: 2015-05-16; просмотров: 1052;
