Геометрическое представление сигналов и помех.

Математический объект A_i является элементом множества А₁.

if над объектом A_i можно произвести линейные операции то множество А₁ принадлежит линейному пространству, а его элементы A_i являются точками этого пространства.

Пространство имеет любую размерность m.

If в таком пространстве определено расстояние м/у точками A_i и A_j то пространство - метрическое, а расстояние м/у началом координат и какой-либо точкой - норма, а пространство нормированное. Соответственно норму и расстояние можно определить. В линейном нормированном пространстве определена норма в виде 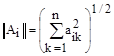и расстояние 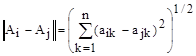-пространство называется Евклидовым. if n→∞ - Гильбертово пространство. A_i – вектор, его длина – норма.

Тогда колебанию U_i(t) можно сопоставить точку A_i или вектор 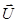в n-мерном пространстве размерность которого равна числу степеней свободы колебания u(t). Пусть колебания u_a(t) и u_b(t) разлагаются по ортогональной системе функций φ_i(t). 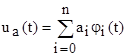, 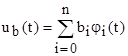Этим колебаниям будут соответствовать вектора 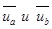с координатами 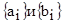. Их длинна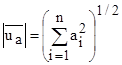 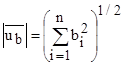. Приняв во внимание условие ортогональности, а точнее ортонормальности. Длина и норма совпадают.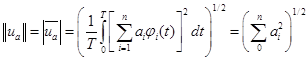

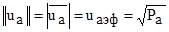
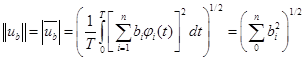
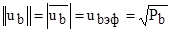P_a и P_b-средняя удельная мощность колебания. Длинна вектора в n-мерном пространстве, определяется эффективным значением соответствующего колебания

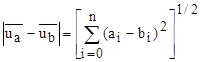-Характеризует степень близости. Расстояние можно рассматривать как модуль разности 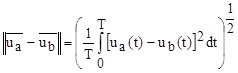, чем меньше эта величина тем меньше различия м/у колебаниями.

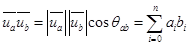* - среднее значение произведения колебаний. 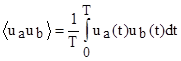**-эффективное взаимодействие м/у колебаниями u_a и u_b.взаимная мощность колебаний-P_ab. If взять в качестве базисной ф-ии 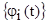, то выражения * и ** совпадут. if u_a и u_b ортогональны <u_au_b>=0. If U_a=–U_b тогда P_ab= – P_a= – P_b. Сигнал и помеху можно представить как вектор. При геометрическом представлении кодированных сигналов. Широко use n-мерное пространство в Неевклидовой метрике. Расстояние в этом пространстве определяется по алгоритму 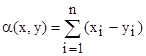, n- число элементов комбинации данного кода, а x_i и y_i –значения соответствующих разрядов. Геометрической моделью n - значного двоичного кода является n-мерный куб с ребром = 1, каждая из вершин которого представляет одну из возможных комбинаций. 000,001,010,100,101,110,011,111 Расстояние - 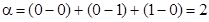. Кодированный сигнал в виде n-мерного куба.