В.4. Представление результатов однократных измерений
Часто для практических целей достаточно произвести однократное измерение интересующей величины. В этом случае невозможно оценить погрешность, связанную со всеми случайными факторами «внешней среды», но мы должны быть уверены, что она достаточно мала. Чтобы убедиться в этом, необходимо хотя бы раз произвести многократное измерение величины и определить случайную погрешность. Но в любом случае остаются погрешности, связанные с использованием для измерения конкретных приборов.
Поэтому результат однократного измерения представляется
в виде
x ± δx,
где x – значение величины, полученное в процессе однократного прямого или косвенного измерения; δx – погрешность однократного измерения.
Количество измерений (одно) и доверительная вероятность P (100 %) в этом случае не указываются, в отличие от результата многократного измерения.
Величина δx в случае прямого однократного измерения представляет собой приборную погрешность (см. п. В.3).
Возникает закономерный вопрос об определении погрешности косвенного измерения в этой ситуации. Перед тем как дать общий рецепт, рассмотрим достаточно простой частный случай такого определения.
Пусть стоит задача измерения объема куба. Самый простой способ решения задачи связан с измерением L – длины ребра куба. После определения длины ребра величина объема куба рассчитывается по формуле
V = L3.
Если измерение L производилось однократно с помощью линейки, то результат такого прямого измерения представляется как
L ± δL,
где L – значение длины ребра, полученное в процессе однократного измерения; δL – погрешность прямого измерения, равная погрешности линейки.
Логично потребовать, чтобы результат косвенного измерения объема имел вид
V ± δV.
Значение объема V рассчитывается по формуле, связывающей его со значением длины ребра L. Остается определить величину δV – погрешность для косвенного измерения объема. Очевидно, эта величина каким-то образом должна быть связана с величиной δL. Чтобы обнаружить эту связь, нам придется снова обратиться к процедуре многократного измерения, но результат, который мы при этом получим, будет справедлив и для однократных измерений.
Пусть в процессе многократных измерений мы получили для одного и того же куба множество значений величины L, измеренной прямым способом, и соответствующее множество величины V, рассчитанной по формуле. Каждому значению Li первого множества соответствует вполне определенное значение Vi второго множества. На рис. В.3 представлен график зависимости V =L3, на котором изображены точки, соответствующие результатам многократных измерений, произведенных для одного и того же куба (разброс значений очень сильно преувеличен). На оси L выделен интервал ΔL, характеризующий разброс значений длины ребра, полученный в процессе многократных прямых измерений. На оси V выделен соответствующий интервал ΔV, характеризующий разброс значений объема, полученный в процессе вычислений. Эти интервалы определяют погрешности измерений величин L
и V. Будем считать, что ΔL и ΔV достаточно малые величины по сравнению со значениями L и V. Тогда их очень просто можно связать между собой. Из треугольника (см. рис. В.3) следует
ΔV = tg(α) ΔL = 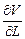 ΔL .
ΔL .
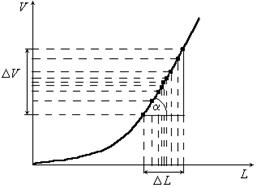
Рис. В.3. Экспериментальные точки на графике
зависимости объема куба от длины его ребра
(разброс значений сильно преувеличен)
Очевидно, для однократного измерения роль ΔL играет погрешность линейки δL, а роль ΔV – интересующая нас величина δV. Поэтому в случае однократного измерения получаем
δV = tg(α) δL = 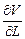 dL ,
dL ,
где значение производной 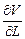 = 3L2 определяется при значении L, полученном в результате однократного прямого измерения.
= 3L2 определяется при значении L, полученном в результате однократного прямого измерения.
Мы получили связь погрешностей прямого и косвенного измерения для частного случая. Обобщим результат на произвольную ситуацию. Пусть величина y определяется из косвенных измерений
(см. п. В.1) и является функцией нескольких независимых величин (независимых переменных), которые в свою очередь измерены либо прямо, либо косвенно. В качестве таких «переменных» могут, в частности, выступать и константы, значения которых определяются и используются при вычислениях с определенной точностью, следовательно, сами константы, так же как и другие величины, характеризуются погрешностью.
Независимые величиныобозначим x1, ..., xn, а соответствующие им погрешности – δx1, ..., δxn. Явный вид функции y = f(x1, ..., xn) должен быть известен. Будем считать, что каждая величина xi вносит свой независимый вклад в погрешность величины y. В таком случае погрешность δy определяется следующим образом:
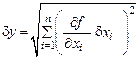 . (В.7)
. (В.7)
В качестве примера рассмотрим определение погрешности для косвенного измерения скорости. Пусть с помощью рулетки мы произвели однократное измерение пройденного телом расстояния x в метрах, а с помощью секундомера – затраченное на это время t в секундах. Погрешность δx в этом случае представляет собой приборную погрешность линейки и является известной величиной. Погрешность δt является приборной погрешностью секундомера. Значение скорости определяется по формуле v = x/t, поэтому скорость является функцией двух величин. В соответствии с общей формулой (В.7) определяем выражение для расчета погрешности скорости
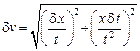 . (В.8)
. (В.8)
Результаты однократных измерений всех трех величин теперь могут быть представлены в стандартной форме (без указания количества измерений и величины доверительной вероятности):
прямые измерения
(x ± δx) м,
(t ± δt) с,
косвенное измерение
(v ± δv) м/с.
Величины δx иδv представляют собой приборные погрешности линейки и секундомера, а величина δv оказывается связанной с ними определенным соотношением (В.8).
В.5. Оформление результатов измерений
При оформлении результатов измерений необходимо придерживаться нескольких простых общепринятых правил. Это сделает Ваши записи наглядными и понятными.
1. Запись результата измерения какой-либо величины требует предварительного округления значений самой величины и ее погрешности. Сначала производится округление погрешности до первой значащей цифры (расчет погрешности должен быть произведен
с точностью до двух значащих цифр). При этом окажется, что первая значащая цифра будет соответствовать определенному порядку или разряду (например, десяткам, единицам, десятым долям и т. п.). После этого производится округление значения измеренной величины до того же самого порядка (разряда). Например, если погрешность составляет единицы, то значение измеренной величины округляется до единиц.
Примеры правильных записей результатов:
L = (125 ± 3) м;
t = (0,067 ± 0,002) c;
g = (9,83 ± 0,01) м/с2 (n = 10, P = 90 %).
2. Если значения измеренной величины и ее погрешности очень малы или велики, то используется показательная форма записи,
в которой за скобки выносится общий десятичный множитель, например:
e = (1,6 ± 0,5) 10–19 Кл,
m = (9 ± 1) 10–31 кг.
3. Результаты большого количества измерений принято заносить в таблицы. В этом случае информация представляется наглядно и компактно. Предварительно необходимо продумать структуру таблицы и последовательность расположения информации в ней.
Таблицы могут быть горизонтального или вертикального исполнения. В первом случае значения одной и той же величины располагаются в строке, во втором – в столбце. При большом количестве измерений чаще используется второй вариант. В начале каждой строки (столбца) пишется название или символ (обозначение) соответствующей величины и указывается единица измерения. Если измеряемые величины очень малы или велики, то используется показательная форма записи чисел. В этом случае десятичный множитель не ставится у каждого значения величины, а выносится в начало строки или столбца и записывается перед единицей измерения.
В качестве примера приведем таблицу, представляющую результаты обработки многократного измерения величины x.
Т а б л и ц а В.2
| i | xi , 10–3 м | 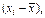 10–3 м 10–3 м
| 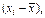 10–6 м2 10–6 м2
|
| 2,1 2,2 1,8 1,7 1,9 | 0,16 0,26 –0,14 –0,24 –0,04 | 0,0256 0,0676 0,0196 0,0578 0,0016 | |
| x = (1,9 ± 0,2)10–3 м (n = 5, P = 90 %) |
Результаты измерений необходимо сразу заносить в заранее подготовленную таблицу.
4. Функциональная зависимость одной величины от другой должна быть представлена графиком. График – самый наглядный способ представления информации в этом случае. Для более надежного построения графиков следует пользоваться миллиметровой бумагой По горизонтальной оси графика принято откладывать значения независимой переменной. По вертикальной – значения функции этой переменной. Прежде чем строить график, определите, чтó в анализируемой ситуации является причиной (ей соответствуют значения независи-
мой переменной), а что – следствием (ей соответствуют значения функции).
В качестве примера на рис. В.4 изображен график зависимости силы тока проводящего элемента от приложенного к нему напряжения.
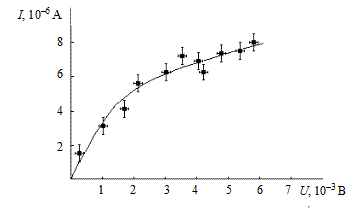
Рис. В.4. Зависимость силы тока проводящего элемента
от напряжения
По каждой оси графика через равные интервалы наносятся масштабные метки. Масштаб для каждой оси выбирается индивидуально. Сначала необходимо определить диапазон изменения значений представляемых величин. Масштаб выбирается так, чтобы экспериментальные точки максимально распределились вдоль каждой из осей. При этом, в частности, необходимо решить, являются ли важными для представления результатов нулевые значения аргумента и функции. Последнее определит значения масштабных меток начала координат (если нули важны, то это будут нулевые метки, если нет – то они не обязательны).
Около координатных осей указывают символы (обозначения) величин и единицы их измерений. При необходимости применения показательной формы записи у единиц измерений ставятся десятичные множители.
Экспериментальные точки наносятся только после того, как поставлены масштабные метки и указаны обозначения осей с единицами измерений. Численные значения величин, соответствующие экспериментальным точкам, на осях не указывают. Сами точки должны быть достаточно выделяющимися.
Если на одних и тех же осях представлено несколько экспериментальных графиков, то для обозначения разных наборов точек рационально использовать разные символьные изображения, например: ●, ○, ■, □, ▲, Δ. При необходимости кроме самих значений величин на графиках указывают соответствующие им погрешности. Это делается с помощью горизонтальных и вертикальных черточек, пересекающих экспериментальные точки (см. рис. В.4). Длина каждой черточки определяется погрешностью измерения соответствующей величины.
По массиву экспериментальных точек проводят «наилучшую» плавную кривую. Не должно быть простого соединения точек ломаной линией. Эти изломы, как правило, не соответствуют действительности.
Существуют специальные математические методы определения «наилучшей» кривой. Вам придется это делать «на глазок», используя три простых принципа:
1) ожидаемая зависимость в лабораторном практикуме чаще всего известна, следовательно, понятно, кривую какого вида надо проводить,
2) кривая должна быть плавной, без изломов (если это не какой-либо специальный случай),
3) кривая должна проходить по массиву экспериментальных точек так, чтобы отклонения разных точек от кривой наилучшим образом компенсировали друг друга (например, точкам, лежащим выше кривой, должны соответствовать точки, лежащие ниже).
Если предварительно рассчитана теоретическая зависимость, то график этой зависимости имеет смысл представить в тех же осях, что и график экспериментальной. Это позволит провести сравнительный анализ ожидаемых и полученных результатов.
В.6. Протокол
Для оформления результатов лабораторных измерений разработана единая универсальная форма – протокол. Он позволяет представить результаты максимально компактно и информативно. Последовательность пунктов протокола отражает ход действий экспериментатора начиная с постановки задачи: формулировка цели конкретной работы, анализ полученных результатов и выводы, вытекающие из этого анализа. Каждый пункт протокола одинаково важен.
Протокол выполняется на одной стороне листа форматом А4. Таблицы, рисунки и графики выполняются карандашом, записи –
авторучкой. Оформление титульного листа протокола приведено на рис. В.5).
|
Рис. В.5. Титульный лист протокола
Ниже приведены основные сведения, касающиеся пунктов протокола.
Дата добавления: 2015-06-17; просмотров: 2786;
