Значения коэффициента Стьюдента
| Р, % | n | |||||||
| 2.0 | 1.4 | 1.3 | 1.2 | 1.2 | 1.1 | 1.1 | 1.1 | |
| 3.1 | 1.9 | 1.7 | 1.5 | 1.5 | 1.4 | 1.3 | 1.3 | |
| 6.3 | 2.9 | 2.4 | 2.1 | 2.0 | 1.8 | 1.7 | 1.7 | |
| 13.0 | 4.3 | 3.2 | 2.8 | 2.6 | 2.3 | 2.1 | 2.0 | |
| 64.0 | 9.9 | 5.8 | 4.6 | 4.0 | 3.3 | 2.9 | 2.7 |
Задав необходимое значение надежности измерения (вероятнос-
ти P), находим по таблице величину tS, соответствующую проведенному количеству измерений n. Например, для P = 80 % при n = 5 значение tS = 1.5.
Величину доверительной погрешности измерения находим по формуле
Δx = tSSx/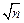 
. (В.5)
Чем большее значение надежности измерения выбирается, тем больше значение коэффициента Стьюдента и тем больше ширина доверительного интервала (больше величина доверительной погрешности). С ростом числа измерений величина tS уменьшается.
Результат многократного измерения представляется в следующей форме:
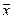± Δx (n = ... , P = ... ).
В скобках указывается количество измерений и значение доверительной вероятности, соответствующее доверительной погрешности.
Такая форма записи наиболее информативна, так как она содержит данные не только о среднем значении измеренной величины и погрешности измерения, но и оценку надежности результата.
Дата добавления: 2015-06-17; просмотров: 701;