Частотная и фазовая модуляция.

Частотная модуляция – изменение во времени пропорционально первичному сигналу S(t) частоты несущего колебания.

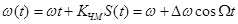(*), где K_ЧМ- коэффициент пропорциональности. 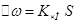- девиация частоты, т.е. максимальное отклонение частоты модулированного сигнала от частоты несущей.

Большему значению амплитуды модулирующего сигнала соответствует большая частота модулированного сигнала.

Фазовая модуляция.(при изменении фазы несущего колебания)

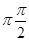
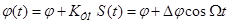, где K_ФМ - коэффициент пропорциональности.

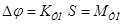- индекс фазовой модуляции.

Между частотной и фазовой модуляцией существует тесная связь.

Представим модулированное колебание в следующем виде:

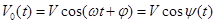
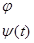-начальная и полная фазы соответственно

Между фазой 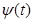и частотной 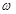существует связь: 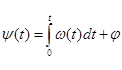; вместо ω(t) выражение со (*)

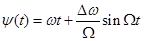
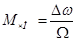- индекс частотной модуляции.

ЧМ: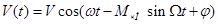

ФМ: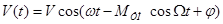

Т.е. по внешнему виду отличить сигналы ФМ и ЧМ трудно, поэтому их называют угловой модуляцией.

М_ЧМ и М_ФМ называют индексом угловой модуляции.

Несущие колебания угловой модуляции можно представить в виде суммы гармонических колебаний:

{ }

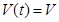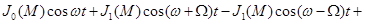
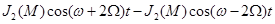
М-индекс угловой модуляции. Амплитуда гармоник определяется некоторыми коэффициентами J_K(M)-функция Бесселя.

Аналитический вид данной функции сложен, поэтому она приведена в справочнике.

Чем больше M, тем шире спектр модулированного колебания.

При гармоническом первичном сигнале S(t) спектр модулированного колебания содержит бесконечное число дискретных составляющих, образующих нижнюю и верхнюю боковые полосы, симметричные относительно несущей.

Если спектр сигнала S(t) занимает полосу от 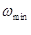до 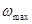и соответствует более сложному чем гармоническое колебание, сигналу, то спектр модулированного колебания будет выглядеть ещё сложнее.