Информационная мера Шеннона
Возвратимся к рис. 1 и рассмотрим функционирование частного случая системы передачи сообщений, состоящей из субъекта – источника языковых (знаковых) сообщений ДИС (источник дискретных сообщений), входного преобразователя 1, который представляет собой печатную машинку или клавиатуру ПК, и ПЗУ, которое представляет собой лист бумаги или ПЗУ ПК. То есть предположим, что субъект-ДИС набирает текст некоторого сообщения, не сте-снённый какими-либо ограничениями по времени набора.
Уточним терминологию и аббревиатуру. По существу, если субъект-ИС вводит в подсистему ПСППС знаковое сообщение, то его следует называть источником знаковых сообщений (ИЗС). Однако в математической теории информации (по инициативе К. Шеннона) установилась традиция называть такие источники дискретными источниками сообщений (ДИС: [46], с. 249). Поэтому, не нарушая традиции, источники ИЗС в дальнейшем мы будем обозначать как ДИС, но называть источниками дискретных (то есть знаковых) сообщений.
Обычно текст состоит из ряда предложений, которые представляют собой некоторые последовательности Si(n) = (ui1, ui2, …, uik, …, uin) знаков (первичных символов) из множества {uj} 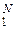 = U – алфавита знаковой системы. Здесь n – длина (количество знаков) i-го сообщения Si(n). При этом на k-м месте последовательности Si(n) знак uj может появиться с вероятностью P(uj) = Pj независимо от того, какие знаки предшествовали ему – в простейшем случае, либо (как в тексте реального языка) – в зависимости от реализации в последовательности Si(n) ряда знаков из множества {uj}
= U – алфавита знаковой системы. Здесь n – длина (количество знаков) i-го сообщения Si(n). При этом на k-м месте последовательности Si(n) знак uj может появиться с вероятностью P(uj) = Pj независимо от того, какие знаки предшествовали ему – в простейшем случае, либо (как в тексте реального языка) – в зависимости от реализации в последовательности Si(n) ряда знаков из множества {uj} 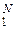 , стоящих до появления очередного знака uik. В последнем случае следует применять вероятностные модели типа цепей Маркова. В первом (простейшем) случае ситуация определяется только совокупностью P ={Pj}
, стоящих до появления очередного знака uik. В последнем случае следует применять вероятностные модели типа цепей Маркова. В первом (простейшем) случае ситуация определяется только совокупностью P ={Pj} 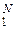 априорных вероятностей появления знаков {uj}
априорных вероятностей появления знаков {uj} 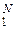 в любой из последовательностей Si(n); i, n = 1, 2, …
в любой из последовательностей Si(n); i, n = 1, 2, …
Понятие количества информации, содержащейся в данном i-м сообщении Si(n), трудно сформулировать на синтактическом (структурном) уровне семиотической системы. На семантическом (смысловом) уровне элементарным сообщением является слово или предложение. Язык позволяет сконструировать практически бесконечное множество предложений. Однако большинство из них не будут иметь смысла – не будут содержать семантической информации.
Чтобы определить количество информации, содержащейся в данном осмысленном предложении, нужно предъявить его субъекту-ПИ и посмотреть на его реакцию (фрагмент информационного взаимодействия двух субъектов в системе ЭТИС – см. разд. 2).
В рамках тезаурусовсубъекта-ДИС и субъекта-ПИ потенциально могут быть сформулированы (сформированы) три типа осмысленных сообщений: предложения, содержащие информацию о достоверных событиях («Великая Французская революция началась 14 июля 1789 г. взятием Бастилии.»), о невозможных («Создан вечный двигателя II рода.») и о неопределённых («Завтра днём ожидается малооблачная погода, временами – дождь; ветер – северный, слабый до умеренного.»).
Пусть субъект-ДИС предъявил субъекту-ПИ сообщение о достоверном(для обоих субъектов) событии. Субъект-ПИ осознал это сообщение – и тут же «выбросил его из головы»:для негоколичество информации, содержащейся в этом сообщении, нулевое.
Пусть субъект-ДИС передал сообщение о событии, которое в тезаурусе субъекта-ПИ имеет большýю априорную вероятность (объективную ожидаемость): (а) «По прогнозу гидрометеоцентра: завтра днём 30 сентября в Санкт-Петербурге ожидается 5-10 градусов тепла». Субъект-ПИ оценит количество семантической информации, содержащейся в сообщении (а), как небольшое. А вот сообщение: (б) «По прогнозу гидрометеоцентра: завтра днём 30 сентября в Санкт-Петербурге ожидается от 10 до 15 градусов мороза» – с точки зрения субъекта-ПИ – содержит большое количество информации (на семантическом уровне семиотики). Если субъект-ПИ не собирается назавтра идти на улицу, то он удивится (реакция субъекта-ПИ на семантическом уровне семиотики), но не предпримет каких-либо особых действий (прагматический уровень семиотики). Если же назавтра ему предстоит выйти из дома, то он не только удивится, но и приготовит тёплую одежду и обувь (прагматический уровень семиотики).
Таким образом,
| количество информации, содержащейся в знаковом сообщении, непосредственно связано с априорной вероятностью реального события, о котором информирует субъекта-ПИ данное сообщение. |
Далее. Если субъект-ПИ получил два никак не связанных между собой сообщения («В огороде – бузина.» и «В Киеве – дядька.»), то количество информации, содержащейся в этих двух сообщениях вместе, должно равняться сумме количеств информации, содержащейся в каждом из них в отдельности: свойство аддитивности информации.
Кроме того, количество семантической информации – величина положительная (неотрицательная), так как бессмысленное предложение или предложение на непонятном субъекту-ПИ языке воспринимается им только как факт наличия языкового сообщения, недоступного для его понимания – третья позиция субъекта-ПИ по отношению к сообщению (см. Прил. 1). А дезинформация в тезаурусе субъекта-ПИ содержит позитивную информацию, если он не знаком с происхождением этого сообщения.
Следовательно,
| насемантическом уровне семиотики количество информации, содержащейся в принятом субъектом-ПИ сообщении, определяется «априорной вероятностью» Pr , с которой оценивает субъект-ПИ в своём тезауруседанное сообщение из бесконечного множества ему подобных. |
| Это количество информации – величина положительная и может изменяться от нуля (при Pr = 1) до произвольно большого значения. Если же субъект-ПИ получил последовательность независимых (никак не связанных между собой) сообщений, то общее количество полученной им информации равно сумме количеств информации, содержащейся в каждом отдельном сообщении. |
Однако этисвойства количественной меры семантические информации не могут быть непосредственно перенесены на синтактическийуровень формально-математических моделей знаковых (семиотических) систем, ибо на этом уровне отсутствуют смысловые (семантические) и ценностные (прагматические) критерии оценки содержания получаемых сообщений. Кроме того, семантические критерии у субъекта-ДИС и у субъекта-ПИ могут быть различными: смысл, который субъект-ДИС вкладывал в данное сообщение, может быть «переосмыслен» субъектом-ПИ или не понят им вовсе. В таких случаях даже при высококачественном канале связи происходит потеря информации при её передаче от источника ДИС к получателю ПИ. Дополнительная потеря информации происходит непосредственно в подсистеме передачи и приёма сообщений ПСППС – по различным причинам: плохое освещение, низкокачественный текст, неразборчивый почерк, помехи в канале связи ПСППС и т. п.
Рассмотрим некоторый идеальный случай статической подсистемы ПСППС: субъект-ИС точно формулирует своё сообщение на выбранном им языке и безошибочно вводит текст этого сообщения (например с помощью клавиатуры ПК) в подсистему ПСППС; подсистема ПСППС без искажений доводит текст до субъекта-ПИ; субъект-ПИ правильно воспринимает текст и правильно интерпретирует переданное сообщение. В этом случае количество переданной субъектом-ИС и принятой субъектом-ПИ информации является функцией только априорной вероятности Pr данного сообщения в их общем тезаурусе, а количество семантической информации, содержащейся в последовательности независимых сообщений, равно сумме количеств информации, содержащейся в каждом из них.
Для математического анализа статических информационных эроготехнических систем, следовательно, можно применить вероятностные модели дискретных событий (см. например [7, 8, 12]). Простейшим понятием в этих моделях является вероятностное пространство {Uε, Pε, Fε}, которое является совокупностью множества Uε независимых элементарных событий εj ( j = 1, 2, …, N ) множества Pε их априорных вероятностей Pj и множества Fε сложных событий Ak, составленных из этих элементарных. Пространство {Uε, Pε, Fε} должно быть дополнено правилами вычисления вероятностей P(Ak) сложных событий по вероятностям Pj элементарных εj.
Для математического анализа технических информационных систем мы можем формально (аксиоматически) перенести количественные свойства информации, выявленные на семантическом уровне семиотики, на синтактический уровень, ибо техническая подсистема информационной эрготехнической системы не может оперировать со смыслами передаваемых сообщений и объективно оценивать субъективные ожидания субъекта-ПИ. Для технических информационных систем – как подсистем ЭТИС – в качестве элементарных событий εj ( j = 1, 2, ..., N ) должны выступать элементарные сообщения uj ( j = 1, 2, ..., N ), выдаваемые источником ДИС, а в качестве их априорных вероятностей Pj – частотности этих сообщений в достаточно длинных последовательностях сообщений Si(n) = (ui1, ui2, …, uik, …, uin), то есть при n → ∞.
Если язык сообщений – письменный, то в качестве такого множества можно было бы взять отдельные слова (иероглифическое письмо). Однако в этом случае количество N элементарных сообщений {uj}  будет неоправданно большим (две-три сотни тысяч). Поэтому лучше всего элементарным сообщением считать отдельный языковый знак: букву, цифру, знак препинания, пробел и т. д. Всего таких «возможных элементарных сообщений» будет менее сотни. Эти языковые элементы назовём элементарными сообщениями(синтактического уровня), илизнаками, или же первичными символами. Ясно, что разбиение знаков на графические элементы (как это делается в иероглифическом письме) является нерациональным.
будет неоправданно большим (две-три сотни тысяч). Поэтому лучше всего элементарным сообщением считать отдельный языковый знак: букву, цифру, знак препинания, пробел и т. д. Всего таких «возможных элементарных сообщений» будет менее сотни. Эти языковые элементы назовём элементарными сообщениями(синтактического уровня), илизнаками, или же первичными символами. Ясно, что разбиение знаков на графические элементы (как это делается в иероглифическом письме) является нерациональным.
Будем считать, что поток элементарных сообщений (сложное сообщение – текст Si(n)), поступающий в статическую подсистему ПСППС, представляет собой последовательность знаков (первичных символов). Частотности появления этих знаков в текстах будут различными. Поэтому информационная модель источника ДИС должна состоять, во-первых, из множества знаков U = {uj}  и, во-вторых, из соответствующего ему множества P = {Pj}
и, во-вторых, из соответствующего ему множества P = {Pj}  априорных вероятностей появления знаков в различных текстах. При этом вероятности Pj можно оценить статистически: для данного типа длинных текстов
априорных вероятностей появления знаков в различных текстах. При этом вероятности Pj можно оценить статистически: для данного типа длинных текстов
Pj = 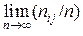 , где ni j – количество знаков uj, содержащихся в любом i-м сообщении Si(n).
, где ni j – количество знаков uj, содержащихся в любом i-м сообщении Si(n).
Отметим, что множество U – не упорядочено (бессмысленно говорить, что буква “а” больше или меньше буквы “я”). Введение на множестве U информационной меры I = {Ij} 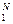 делает его (линейно) упорядоченным, а значит – измеримым. То есть про любые два различные элемента uj
делает его (линейно) упорядоченным, а значит – измеримым. То есть про любые два различные элемента uj  U и ul
U и ul  U можно будет сказать, что один из них (скажем uj) содержит не меньше информации, чем другой (например ul): I(uj) ≥ I(ul), или Ij ≥ Il. При этом элемент uj содержит больше информации, чем ul, на [I(uj) – I(ul)] единиц информации.
U можно будет сказать, что один из них (скажем uj) содержит не меньше информации, чем другой (например ul): I(uj) ≥ I(ul), или Ij ≥ Il. При этом элемент uj содержит больше информации, чем ul, на [I(uj) – I(ul)] единиц информации.
В естественных языках вероятности Pj появления элементарных сообщений (знаков uj  U) зависят не только от их априорных вероятностей (частотностей) Pj
U) зависят не только от их априорных вероятностей (частотностей) Pj  P, но и от того, какой текст был набрандо появления данного знака. В простейшем (идеализированном) случае будем считать, что появление данного знака uj
P, но и от того, какой текст был набрандо появления данного знака. В простейшем (идеализированном) случае будем считать, что появление данного знака uj  U в данном месте текста не зависит от реализации предыдущей части текста. Тогда простейшая знаковая (семиотическая, «дискретная») информационная модель источника ДИС {U, P, I, S} будет состоять из:
U в данном месте текста не зависит от реализации предыдущей части текста. Тогда простейшая знаковая (семиотическая, «дискретная») информационная модель источника ДИС {U, P, I, S} будет состоять из:
• конечного множества (алфавита) элементарных сообщений (знаков, первичных символов) U = {u1, u2, …, uj, …, uN };
• множества P = {Pj}  априорных вероятностей (частотностей) их появления в разных местах различных текстов;
априорных вероятностей (частотностей) их появления в разных местах различных текстов;
• множества S последовательностей Si(n) (i = 1, 2, …, N n) элементарных сообщений (Si(n)  S) вида Si(n) = (ui1, ui2, …, uik, …, uin ), то есть множества всех возможных сообщений длины n = 1, 2, …;
S) вида Si(n) = (ui1, ui2, …, uik, …, uin ), то есть множества всех возможных сообщений длины n = 1, 2, …;
• информационного множества I = {I1, I2, …, Ij, …, IN}, где Ij – количество информации, заключающейся в элементарном сообщении (знаке) uj  U;
U;
а также содержать правила вычисления количества информации I(Si(n)), заключающейся в любом из сообщений Si(n)  S.
S.
Определим величину количества информации I(u) для элементарного «дискретного» сообщения (знака) u  U, имеющего априорную вероятность или частотность P.
U, имеющего априорную вероятность или частотность P.
Ясно, что семантического смысла знак “u” не имеет. Поэтомуперенесём формально основные свойства семантической информационной меры на синтактический уровень в качестве постулатов(декларируемых утверждений).
То есть положим, что:
1) величина I(u) является некоторой функцией I(u) = f (P) от априорной вероятности P элементарного сообщения u  U, котораядолжна обладать следующиминеобходимымисвойствами;
U, котораядолжна обладать следующиминеобходимымисвойствами;
2) f (P) ≥ 0, то есть количество информации в любом элементарном сообщении u  U неотрицательно; f (P) = 0 только при P = 1; при P = 0 значение функции f (P) не определено ( f (0) = + ∞);
U неотрицательно; f (P) = 0 только при P = 1; при P = 0 значение функции f (P) не определено ( f (0) = + ∞);
3) если имеется совокупность двух элементарных сообщений, то есть uj  U и ul
U и ul  U, с априорными вероятностями Pj = P(uj) и Pl = P(ul) и если Pl > Pj, то f (Pl) < f (Pj), то есть функция f (P) – строго убывающая.
U, с априорными вероятностями Pj = P(uj) и Pl = P(ul) и если Pl > Pj, то f (Pl) < f (Pj), то есть функция f (P) – строго убывающая.
Общий вид функции f (P), удовлетворяющей постулатам 1)–3), для наглядности приведён на рис. 2.

 бит I Таких функций f (P) существует
бит I Таких функций f (P) существует
бесконечное множество. Однако, ис-
 3 ходя из семантического принципа ад-
3 ходя из семантического принципа ад-
дитивности информации, для однозна-
 2 f (P) чного определения функции f (P) дос-
2 f (P) чного определения функции f (P) дос-
таточно ввести ещё один (четвёртый)



 1 постулат:
1 постулат:
4) f (Si(2)) = f [P(uj, ul)] = f (Pj ∙ Pl) = f (Pj) + f (Pl),


 то есть количество информации, содер-
то есть количество информации, содер-
0 0,5 1,0 P жащейся в любой i-й последовательнос-
Рис. 2. Зависимость количества ти Si(2) = (uij, uil) из двух элементарных
информации I от априорной вероят- независимых сообщений uj  U и ul
U и ul  U,
U,
ности P выдачи источником ДИС равно сумме количеств информации, со-
элементарного сообщения u  U держащейся в каждом из них в отдель-
U держащейся в каждом из них в отдель-
ности (аддитивность информационной
меры). К. Шеннон показал, а А. Я. Хинчин математически строго доказал, что единственной функцией, удовлетворяющей всем четырём постулатам 1)– 4), являетсялогарифмическая функция: I(u) = – K log a P(u), где K > 0.
Итак,
количество синтактической информации I(u),
содержащейся в некотором знаке u  U, который имеет
априорную вероятность появления в любом месте
i-й последовательности Si(n) =( ui1, ui2, …, ui k, …, ui n) U, который имеет
априорную вероятность появления в любом месте
i-й последовательности Si(n) =( ui1, ui2, …, ui k, …, ui n)  S
независимых элементарных сообщений (знаков) длины n,
определяется формулой I(u) = – K log a P(u),
где K – некоторая положительная константа. S
независимых элементарных сообщений (знаков) длины n,
определяется формулой I(u) = – K log a P(u),
где K – некоторая положительная константа.
|
Поскольку величина P оценивается статистически, мера I(u) называется статистической информационной мерой Шеннона.
С помощью построенной информационной модели {U, P, I, S} источника ДИС можно проводить самые различные информационные расчёты. Остаётся договориться о единицах измерения количества синтактической информации Ij = – K log a Pj в знаковой системе U = {uj}  .
.
Для простоты вычислений, как это принято в физических дисциплинах, лучше всего положить K = 1. Если в качестве основания a логарифмов выбрать число 2, то такие единицы называютсябитами(bit = BInary uniT – двоичная единица, или BInary digiT – двоичная цифра); если трансцендентное число e ≈ 2,7183 – тонатами(натуральные единицы); если a = 10 – тодитами(десятичными единицами, или Хартами – в честь упомянутого ранее Р. Хартли).
За последние полвека наибольшее распространение в качестве единиц количества информации получилибиты.
Количество битов информации I(u), содержащейся в элементарном сообщении u  U, которое выдаётся источником ДИС с априорной вероятностью P(u), равно I(u) = – log 2 P(u) (бит). Один бит информации I(u) = 1 содержится в сообщении u, имеющем априорную вероятность появления в тексте P(u) = 0,5 (см. рис. 2): I0(1/2) = – log 2 (1/2) = log 2 2 = 1 (бит).
U, которое выдаётся источником ДИС с априорной вероятностью P(u), равно I(u) = – log 2 P(u) (бит). Один бит информации I(u) = 1 содержится в сообщении u, имеющем априорную вероятность появления в тексте P(u) = 0,5 (см. рис. 2): I0(1/2) = – log 2 (1/2) = log 2 2 = 1 (бит).
В литературе по теории информации обычно не оговаривают каждый раз основание логарифма в выражении I(u) = – log a P(u). Если в качестве единиц информации имеют в виду натуральные, то пишут I(u) = – ln P(u) (нат); если десятичные, то пишут I(u) = – lg P(u) (дит, или Харт); если же двоичные – то просто I(u) = – log P(u) (бит).
Вопросы для самопроверки
1. Какие основные типы сообщений существуют на семантическом уровне семиотики?
2. Что такое свойство аддитивности информации?
3. Каково определение понятия «количество семантической информации»?
4. Какова простейшая информационная модель источника знаковых (дискретных) сообщений?
5. Каковы первые три постулата математической теории информации и что они определяют?
6. В чём смысл четвёртого постулата (постулата аддитивности) математической теории информации?
7. Каковы основные единицы измерения синтактической информации?
Дата добавления: 2015-05-16; просмотров: 966;
