Алгоритм Хаффмена
Алгоритм Хаффмена8)використовує особливий вид подання елементів - префиксный код. Префиксный код - це код змінної довжини, що володіє особливою властивістю - властивістю префікса: менш короткі коди не збігаються із префіксом (початковою частиною) більше довгих. Такий код дозволяє здійснювати взаємо-однозначне кодування. Відповідно, потрібно побудувати спосіб стиску, що використовує префиксный код і при цьому обеспечивающий максимально можливий ступінь стиску. Формалізуємо завдання.
Дано на вході:
Алфавіт A = {a1, . . . , an}.
Безліч P = {p1, . . . , pn} - розподіл імовірностей появи або таблиця кількостей елементів з A, pi = Prob(ai), 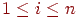 . Далі
. Далі 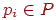 будемо називати вагою ai.
будемо називати вагою ai.
Необхідно на виході:
Код (алфавіт) H(A, P) = {h1, . . . , hn} - набір кодів (далі бінарних), так що hi = Code(ai), 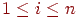 .
.
Завдання:
Нехай 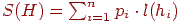 , де l(hi) - довжина коду hi. S(H) - зважена довжина шляху (пояснення даного терміна див. нижче).
, де l(hi) - довжина коду hi. S(H) - зважена довжина шляху (пояснення даного терміна див. нижче).
Потрібно, щоб H було оптимально, тобто
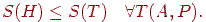
Алгоритм Хаффмена є рішенням даного завдання [36], [37].
Побудова набору кодів звичайно здійснюється за допомогою так званих кодових дерев. Припустимо, що використовуються бінарні коди, тоді дерево буде бінарним (у загальному випадку ступінь розгалуження залежить від підстави системи числення подання кодів). Термінальні вузли дерева містять сам елемент алфавіту, його вагу, посилання на батьківський вузол (втім, це залежить від конкретної реалізації). Внутрішні вузли містять суму ваг своїх вузлів-нащадків, посилання на вузли-нащадки й, можливо, посилання на батьківський вузол. Ребрам дерева зіставляються нуль і одиниця, для лівих і правих відповідно. Повністю добудоване дерево має n термінальних вузлів і n - 1 внутрішніх. Роблячи прохід від кореня до термінального вузла й виписуючи по шляху 0 і 1 для ребер, що зустрічаються, одержимо код елемента в термінальному вузлі.
Тепер став зрозумілий зміст назви S(H), тому що довжина коду l(hi) суть довжина шляхи від кореня до відповідної термінальної вершини.
Опишемо алгоритм побудови кодового дерева Хаффмена.
1. Створити n термінальних вузлів по числу елементів в алфавіті. У кожний вузол записати відповідні ваги.
2. Створити батьківський вузол і з'єднати з ним два вільних (тобто не батьки, що мають) вузла з мінімальними вагами, записавши в нього суму ваг безпосередніх нащадків.
3. Якщо кількість вільних вузлів більше одного, то перейти до пункту 2. Інакше даний вузол - корінь дерева Хаффмена.
Процес стиску полягає в заміні кожного елемента вхідної послідовності його кодом. Стиснемо наступний рядок "TOBEORNOTTOBE".
1. Складемо таблицю ваг:
| елемент алфавіту | T | O | B | E | R | N |
| вага |
2. Побудуємо дерево Хаффмена (см. рис. 13.1):
- проинициализируем дерево термінальними вузлами,
- створимо батьківський вузол N1 для вузлів елементів "N" і "R" з вагою 2;
- створимо батьківський вузол N2 для вузла елемента "E" і вузла N1 з вагою 4;
- створимо батьківський вузол N3 для вузлів елементів "Т" і "B" з вагою 5;
- створимо батьківський вузол N4 для вузла елемента "O" і вузла N2 з вагою 8;
- створимо батьківський вузол N5 для вузлів N3 і N4 c вагою 13.
3. Проведемо кодування. Складемо для зручності таблицю кодів:
| елемент алфавіту | T | O | B | E | R | N |
| код |
4. Отже, одержимо послідовність "10 00 11 010 00 0110 0111 00 10 10 00 11 010".
Отримана послідовність має довжину 32 біта. Вихідна, якщо вважати алфавітом набір ASCII - 104 біта, якщо вважати алфавітом тільки набір "TOBERN" - 39 біт.
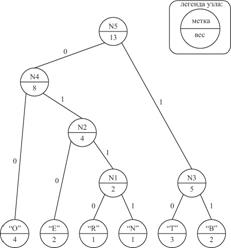
Рис. 13.1. Приклад дерева Хаффмена.
Помітимо, що в процесі побудови дерева виникала неоднозначність у виборі двох вузлів для обробки. У нашім прикладі вибір був зроблений на користь наочності подання, однак ніякого впливу на якість стиску воно не робить.
Декодування здійснюється прямою заміною коду на відповідний елемент. І в силу того, що використано префиксный код, не потрібно відзначати початок і кінець чергового коду.
Наведений вище алгоритм є двухпроходным. Перший прохід по зображенню створює таблицю кількостей (ваг) елементів, а під час другого відбувається кодування. Існують реалізації алгоритму з фіксованою таблицею (CCITT Group 3 - використовується для передачі факсимільних зображень). Часто буває, що нам невідомо апріорний розподіл імовірностей елементів алфавіту, тому що нам не доступна вся послідовність відразу. Або, наприклад, бажано позбутися від необхідності зберігати таблицю ваг для декодування. Відповідно, були запропоновані адаптивні модифікації алгоритму Хаффмена.
Розглянемо модифікацію алгоритму, у якій дерево будується в міру надходження нових елементів так, щоб зберігалася впорядкованість по вагам вузлів. Упорядкованість наступного виду: при проході кожного рівня дерева, починаючи з нижнього ліворуч праворуч, ваги вузлів не убувають. Побудова дерева виконується в такий спосіб.
- На першому кроці будується звичайне дерево Хаффмена, уважаючи, що ваги всіх вершин рівне (таке дерево буде впорядкованим у зазначеному вище змісті).
- При надходженні чергового елемента виконується наступне:
- елемент кодується;
- збільшується значення ваги у відповідному термінальному вузлі;
- збільшуються значення ваг у відповідних вершинах по шляху від цього вузла до кореня;
- якщо після цього впорядкованість дерева порушена, то:
- для такого вузла (А) серед сусідів праворуч шукається крайній вузол (Б), вага якого менше;
- вузли А и Б міняються місцями, при цьому ваги вузлів на шляхах від переставлених до кореня коректуються відповідним чином;
- якщо дерево знову з, то знову виконується попередній крок.
Декодування виконується за аналогічною схемою: ініціалізація дерева, одержання коду, розшифровка, відновлення дерева, перебудова дерева (якщо необхідно), і т.д.
Алгоритм Хаффмена використовується на одній зі стадій стиску у форматі JPEG, як складова частина методу DEFLATE, а також у багатьох інших універсальних кодерах. Хоча даний метод уступає по ступені стиску арифметичному кодуванню, його простота, швидкість і термін, що закінчився, дії патентів забезпечують широку поширеність.
Дата добавления: 2015-04-03; просмотров: 1403;
