Зображення як функція

Будемо розглядати зображення як функцію двох змінних, певну в крапках кінцевого растра (мається на увазі крапкова модель растра, див. визначення в I(x, y) - значення атрибута пикселя (наприклад номер у палітрі, інтенсивність), що залежить від колірної моделі подання зображення (див. мал. 14.1 і мал. 14.2). Безліч таких функцій на крапках фіксованого кінцевого растра утворять конечномерное евклидово простір R^X,Y розмірності m × n (|X|=m,|Y|= n) зі скалярним добутком

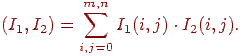
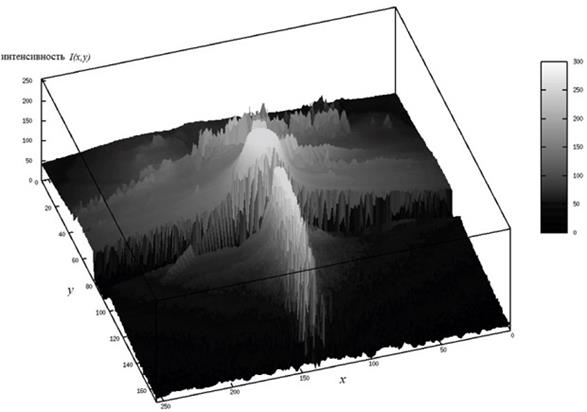
Рис. 14.2. Зображення як функція двох змінних

Будемо ототожнювати з таким простором L₂(X × Y ). У такому просторі існує базис (див. [3]), тобто така система елементів 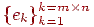з R^X,Y і такий набір не рівних одночасно нулю коефіцієнтів 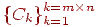, що для будь-якої функції I із цього простору виконане

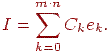
Якщо додатково припустити ортонормальность базису, тобто

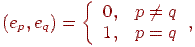
те виконується наступне співвідношення:

C_k = (I, e_k).