Зображення

При розгляді зображення, створеного у ПЕМ, було виявлено, що навіть прості уявлення про природу виникнення контрасту на зображенні не можна пояснити без використання хвильових властивостей електронів. Механізм формування зображення освітленого тіла плоскопаралельним пучком електронів можна описати з використанням теорії Аббе. Суть її полягає в тому, що в задній фокальній площині лінзи формується дифракційний розподіл амплітуд розсіяного об’єктом випромінювання (дифракція Фраунгофера). Тобто кожна точка задньої фокальної площини розглядається як джерело хвиль Гюйгенса, які поширюються до площини зображення. Згідно з принципом Гюйгенса всі точки поверхні, через яку проходить фронт хвилі, можна розглядати як джерело вторинних когерентних хвиль. Розподіл амплітуд у площині зображення визначається сумою всіх хвиль Гюйгенса, джерелом яких є задня фокальна площина лінзи.

Принцип формування зображення з використанням теорії Аббе можна зрозуміти у випадку, коли об’єкт є одномірною періодичною граткою з періодом а. На рис. 3.4 ілюструється картина формування зображення періодичної гратки об’єктивною лінзою.

Електрони, які розсіяні решіткою під різними кутами, дають дифракційні максимуми у точках 0, 1, -1, 2, -2 і т.д. на апертурній площині. Для точок 0, 1, -1 і т.д. кути розсіювання будуть визначатися за співвідношенням

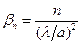, (3.6)

де n – порядок відбиття; l– довжина хвилі електрона.

Максимуми у задній фокальній площині характеризуються комплексними амплітудами хвиль φ_0, φ_ne^iχ(n), φ_ne^-iχ(n) (c – фаза) і розміщені в точках, координати яких відповідають умові

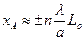. (3.7)

Амплітуда y(x_з) у довільній точці на площині зображення являє собою суму комплексних амплітуд усіх

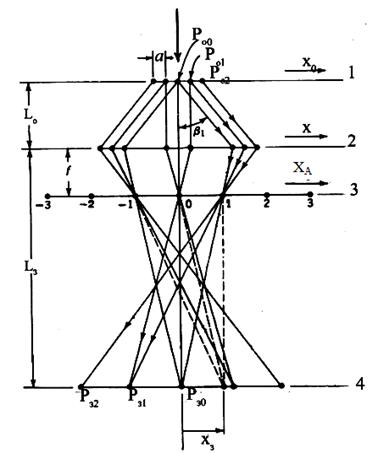
Рисунок 3.4 – Хід променів при формуванні зображення гратки з періодом а: 1 - площина об’єкта; 2 - лінза; 3 – апертурна площина; 4 - площина зображення

хвиль, які поширюються із точок у задній фокальній площині. Амплітуда у кожній n-ій точці площини зображення буде описуватися співвідношенням:

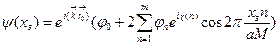, (3.8)

де 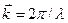– хвильовий вектор; M – збільшення; 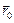– радіус-вектор, проведений із центра хвилі в точку P₃₀.

Інтенсивність у довільній точці на зображенні являтиме собою добуток амплітуди на її комплексно спряжену величину, тобто

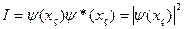. (3.9)

Проаналізуємо розподіл інтенсивностей у площині зображення, розглянувши лише спектри двох порядків n = 0, n = 1, n = -1. У результаті інтенсивність у точках на зображення матиме вигляд

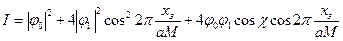. (3.10)

Аналіз співвідношення (3.10) показує наступне.

1 Якщо вважати, що при розсіюванні хвилі фаза χ змінюється приблизно на p/2, то на сфокусованому зображенні інтенсивність буде змінюватися з періодом аМ/2. Дійсно, cos2p(x_з/aM) буде мати максимум, коли 2p(x_з/aM)=±p, звідки x_зmax=±(aM/2). При значенні фази 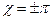до періоду гратки об’єкта на зображенні додається ще половина періода. Таким чином, період зображення гратки становить аМ,тобто він пропорційний збільшенню лінзи.

2 Якщо вилучити нульовий порядок, то у формулі (3.10) перший та останній доданки дорівнюватимуть нулю і спостерігатиметься зображення з періодом aM/2.

3 Якщо у площину зображення будуть надходити хвилі лише із точок 0 та 1, то спостерігатиметься зображення з періодом aM, але зміщене вбік.

4 Якщо пропускати лише один будь-який максимум, то розподілу інтенсивностей на зображенні не буде, тобто зображення буде неперіодичним і, як наслідок, гратка не спостерігатиметься.