Зображення відрізка з нецілочисловими координатами кінців
Для відрізка з нецілочисловими координатами кінців будемо будувати відповідну 4-зв'язну лінію на растрі.
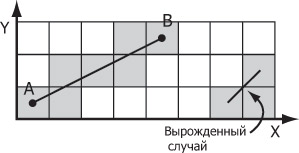
Рис. 6.5. Малювання відрізка з нецілочисловими координатами кінців.
Існує два підходи.
1. Округлити координати кінців до целочисленных і скористатися алгоритмом для цілочислового случаючи. Недолік: може викликати істотні перекручування (особливо у випадку відрізків невеликої довжини).
2. Перейдемо до нашого канонічного випадку, що тепер характеризується тим, що відрізок лежить у першому октанті, але координати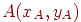 
в цьому випадку: 
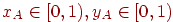. Параметризуємо наш відрізок стандартним образом:
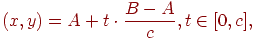
де A і B - кінцеві крапки, c > 0 - якийсь масштабний коефіцієнт. Зробимо c досить більшим цілим числом, щоб зменшити помилки округлення. Тоді розглянемо
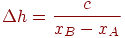
- збільшення t, при зрушенні на 1 піксель по x;
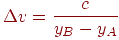
- збільшення t, при зрушенні на 1 піксель по y.
Будемо порівнювати поточні значення h і v, а потім, залежно від цього, робити крок по x або y і надавати відповідні збільшення h і v. Алгоритм закінчиться, коли h або v перевищить c.
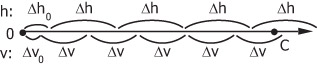
Рис. 6.6. Зміна параметрів h і v.
x = 0; y = 0; // Канонічний випадок: початкова крапка// лежить в [0, 1)
[0, 1) /* Збільшення t, що відповідають зсувам від початковоїкрапки до границь першого пікселя. */ h = ?h * (1 - x); // ?h0v = ?v * (1 - y); // ?v0 while( (h < c) AND (v < c) ){ plot(x, y); if( h < v ) { // Зрушення по горизонталі x++; h += ?h; } else if( h > v ) { // Зрушення по вертикалі y++; v += ?v; } else { // h = v : Вироджений випадок (див. мал. 6.5) // малюємо довільний із двох можливих пикселей, // наприклад, верхній: plot(x,y+1); x++; y++; h += ?h; v += ?v; }} Лістинг 6.4. Алгоритм відображення відрізка з нецілочисловими координатами кінців
Зауваження. Наведений вище алгоритм легко узагальнюється на n-мірний випадок.
Дата добавления: 2015-04-03; просмотров: 1063;