Алгоритм Брезенхема растрової дискретизації відрізка

При побудові растрового образа відрізка необхідно, насамперед, установити критерії "гарної" апроксимації. Перша вимога полягає в тому, що відрізок повинен починатися й кінчатися в заданих крапках і при цьому виглядати суцільним і прямим (при досить високому дозволі дисплея цього можна домогтися). Крім того, яскравість уздовж відрізка повинна бути однакової й не залежати від нахилу відрізка і його довжини. Ця вимога виконати складніше, оскільки горизонтальні й вертикальні відрізки завжди будуть яскравіше похилих, а постійна яскравість уздовж відрізка знову ж досягається на вертикальних, горизонтальним і нахилених під кутом в 45° лініях. І, нарешті, алгоритм повинен працювати швидко. Для цього необхідно по можливості виключити операції з речовинними числами. З метою прискорення роботи алгоритму можна також реалізувати його на апаратному рівні.

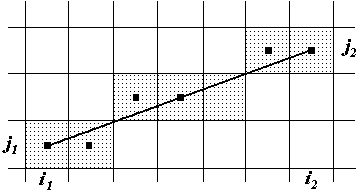
Рис. 10.1. Растровий образ відрізка

У більшості алгоритмів використовується покроковий метод зображення, тобто для знаходження координат чергової крапки растрового образа наращивается значення однієї з координат на одиницю растра й обчислюється збільшення іншої координати.

Завдання полягає в побудові відрізка, що з'єднує на екрані крапки з координатами 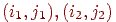(будемо вважати, що 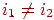). Для побудови відрізка прямій на площині з речовинними координатами можна скористатися рівнянням прямої, що проходить через дві задані крапки, що має вигляд

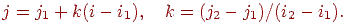
Тепер, уважаючи, що 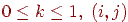- координати поточної крапки растрового образа, а 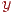- точне значення координати крапки відрізка, можна побудувати наступну крапку:

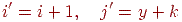
Варто помітити, що целочисленная координата 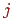зміниться тільки в тому випадку, якщо y перевищить величину 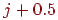( 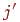є найближче до 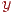ціле число, отримане в результаті операції округлення). Наведений приклад включає операції з речовинними числами, які виконуються істотно повільніше, ніж відповідні целочисленные операції, а при побудові растрового образа відрізка бажаний алгоритм, по можливості обращающийся тільки до целочисленной арифметики. Крім того, алгоритм повинен працювати при будь-якому взаємному розташуванні кінців відрізка.

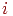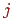Алгоритм Брезенхема побудови растрового образа відрізка був споконвічно розроблений для графобудівників, але він повністю підходить і для растрових дисплеїв. У процесі роботи залежно від кутового коефіцієнта відрізка наращивается на одиницю або , або , а зміна іншої координати залежить від відстані між дійсним положенням крапки й найближчою крапкою растра (зсуву). Алгоритм побудований так, що аналізується лише знак цього зсуву.

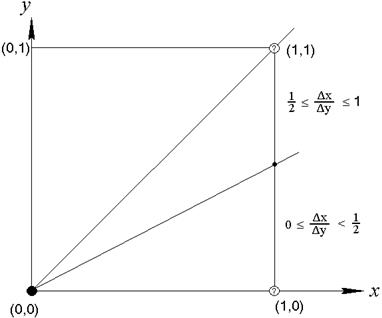
Рис. 10.2. Зв'язок кутового коефіцієнта з вибором пикселя

На мал. 10.2 це ілюструється для відрізка з кутовим коефіцієнтом, що лежить у діапазоні від нуля до одиниці. З малюнка можна помітити, що якщо кутовий коефіцієнт 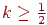, то при виході із крапки 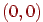перетинання із прямої буде ближче до прямої 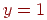, чим до прямої 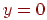. Отже, крапка растра 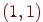краще апроксимує проходження відрізка, чим крапка 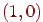. При 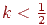вірно зворотне.

На мал. 10.3 показано, яким образом будуються крапки растра для відрізка з тангенсом кута нахилу 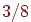, а на мал. 10.4 - графік зсуву. На початку побудови зсув покладається рівним 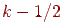, а потім на кожному кроці воно наращивается на величину 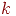, і якщо при цьому вертикальна координата крапки растра збільшується на одиницю, то зсув у свою чергу зменшується на одиницю.

На мал. 10.5 наведена блок-схема алгоритму для випадку 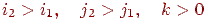. Неважко зрозуміти, як від цього алгоритму перейти до целочисленному: досить замість величини зсуву 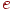перейти до величини .

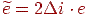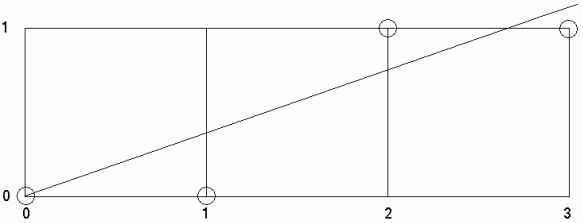
Рис. 10.3. Пиксели, що належать розгорненню відрізка

Рис. 10.4. Графік зміни відхилення

Приведемо загальний алгоритм Брезенхема, що враховує всі можливі випадки напрямку відрізка, розглянутого як вектор на координатній площині (на мал. 10.6 виділені чотири області й зазначені особливості алгоритму в кожній з них).

В описі алгоритму використовуються наступні функції:

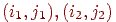Передбачається, що кінці відрізка не збігаються й що всі використовувані змінні є цілими.

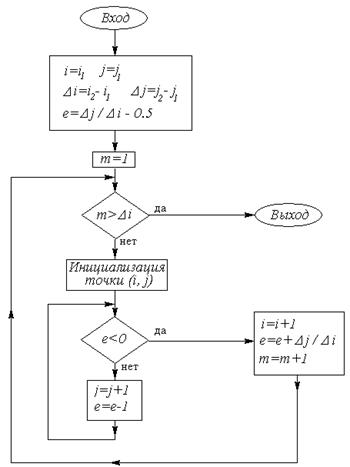
Рис. 10.5. Блок-схема однієї галузі алгоритму Брезенхема

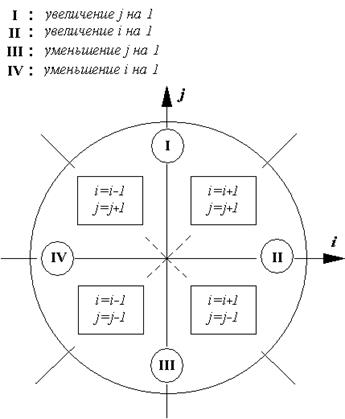
Рис. 10.6. Чотири можливих напрямки відрізка